Глава 4. Функциональные отношения

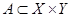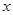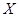Отношение называется функциональным, если все его элементы (упорядоченные пары) имеют различные первые координаты. Иначе говоря, каждому элементу из такому, что 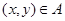соответствует один и только один элемент 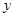из .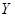

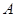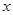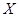Очевидно, для функционального отношения каждое сечение по из содержит не более одного элемента. Если 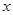не входит в область определения 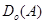этого отношения, то сечение по 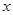пусто. Если сечение по любому элементу из 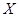содержит один и только один элемент, то функциональное отношение является всюду определенным.

Всякое функциональное отношение можно рассматривать как функцию. При этом первая координата 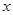упорядоченной пары 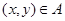является аргументом (переменной), а вторая 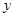– образом (значением) функции. Обычная запись 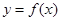соответствует соотношению 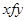или 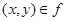. Следует различать функцию 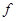как множество упорядоченных пар (отношение) и значение функции 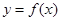как вторую координату одной из таких пар.

Для всякого функционального отношения 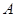можно определить связанную с этим отношением функцию 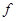. Но симметричное к нему отношение 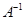может и не быть, функцией.

Если функциональное отношение 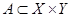всюду определено на 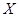, т. е. его область определения 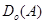совпадает с множеством 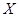, его называют отображением множества 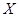в 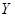и записывают 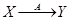. Отображение можно также рассматривать как функцию 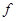, определенную на множестве 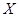и принимающую значения в множестве .

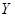Как видно, различие между отображением и функцией сводится к способу определения этих отношений на множестве 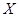, причем отображение следует рассматривать как частный случай функции.

При отображении 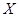в 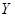каждый элемент 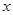из 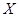имеет один и только один обра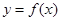з из 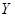. Однако вовсе не обязательно, чтобы и всякий элемент из 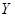был образом некоторого элемента из 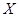(рис. 5а). Если же любой элемент из 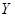есть образ, по крайней мере, одного элемента из 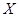(рис. 5б), то говорят, что имеет место отображение 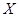на 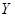(сюръекция или накрытие).

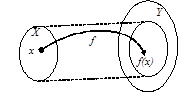
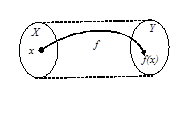
а	б
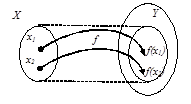
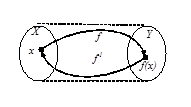
в	г
Рис. 5

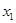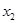Если для любых двух различных элементов и из 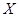их образы 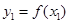и 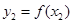также различны, то отображение 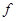называется инъекцией (рис. 5в). Отображение, которое является одновременно сюръективным и инъективным (рис. 5г), называется биекцией (наложением). В этом случае говорят, что есть взаимнооднозначное отображение, а между элементам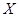и и 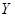имеется взаимно-однозначное соответствие. 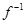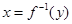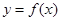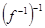При этом, обратное отношение также взаимно-однозначное отображение, равносильно и совпадает с .

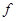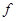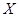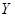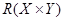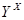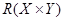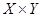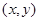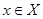Любое отображение из в есть элемент множества , которое обозначается также через (следует напомнить, что – это множество всех подмножеств прямого произведения , а элементами последнего являются упорядоченные пары , где и 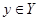. Если 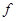– взаимно-однозначное отображение, а множества 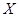и 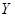совпадают ( 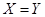), то называют отображением множества 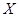на себя. Элементы 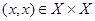образуют тождественное отображение 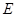, причем .

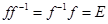Два множества, между элементами которых имеет место биективное (взаимнооднозначное) отображение, называют равномощными.

Мощность конечного множества выражается количеством его элементов, которое называют кардинальным числом. Подсчет элементов конечного множества состоит в установлении взаимнооднозначного соответствия между этими элементами и некоторой последовательностью натуральных чисел, начиная с единицы.

Бесконечные множества также могут различаться по мощности. Наименьшую мощность имеют счетные множества, т. е. такие множества, которые равномощны множеству натуральных чисел. К ним относятся, например, множество всех четных чисел, множество квадратов целых чисел и т. п. Мощность множества действительных чисел отрезка 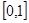, называемая мощностью континуума, превышает мощность счетного множества.

Можно указать множества, мощность которых больше мощности континуума. Но множества с наибольшей мощностью не существует (подобно тому, как не существует наибольшего натурального числа). Это является следствием того, что мощность множества всегда строго меньше мощности множества 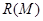всех его подмножеств. Иначе говоря, какой бы мощности не было данное множество, всегда можно образовать множество его подмножеств, которое будет иметь большую мощность. Так, 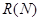, где 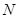– множество натуральных чисел, несчетно: его мощность равна мощности континуума.

В общем случае при отображении элемент из 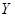может быть образом не одного, а нескольких элементов множества 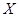. Пусть, например, 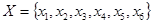и 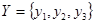, а функциональное отношение 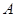имеет вид 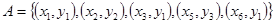. Тогда для этого отношения элемент 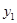является образом элементов 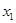, 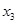и 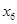. Совокупность всех элементов, образом которых является данный элемент 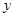из 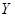, называется полным прообразам элемента 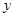и обозначается 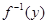. В приведенном примере .

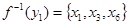Основные свойства отображений выражаются соотношениями:

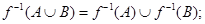
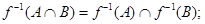
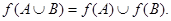
Образ пересечения двух множеств, вообще говоря, не совпадает с пересечением их образов, но можно показать, что

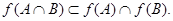
Введенные понятия можно проиллюстрировать на функциях, определенных на числовых множествах, элементами которых являются действительные числа. Такая функция каждому числу 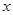из области определения ставит в соответствие число 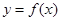из области ее значений. Иначе говоря, числовая функция 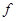определяется множеством упорядоченных пар чисел 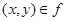. На геометрическом языке множеству действительных чисел соответствует множество точек прямой (числовой оси). Пары чисел 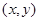представляются в декартовой системе координат точками плоскости с координатам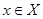и и 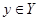, причем первая координата 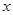– абсцисса, а вторая 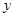– ордината точки. Числовые оси, соответствующие множествам 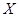и 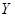, являются осями координат, а декартово произведение 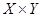, представляет собой множество точек плоскости. Таким образом, между элементами множества 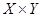и точками плоскости устанавливается взаимнооднозначное соответствие.

Различные подмножества действительных чисел, на которых определяется функция, соответствуют подмножествам точек прямой. В качестве таких подмножеств часто используют следующие: отрезок (замкнутый интервал) 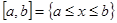; полуинтервал, открытый слева 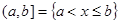; полуинтервал, открытый справа 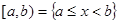, и открытый интервал (или просто интервал) 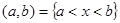. Область определения функции может быть задана и отдельными точками числовой прямой.