Индуктивность контура. Самоиндукция

Явление электромагнитной индукции. Закон Фарадея

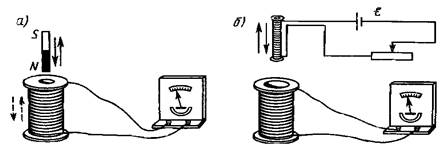
Изложенные ранее экспериментальные факты показывают, что электрические токи создают в окружающем пространстве магнитное поле. Существует и обратное явление: магнитное поле вызывает появление электрических токов. Это явление было открыто после многочисленных экспериментов М. Фарадеем[1] в 1831 г. и получило название электромагнитной индукции. Суть опытов Фарадея можно проиллюстрировать с помощью рис. 8.1. Если постоянный магнит вдвигать и выдвигать из проволочной катушки (соленоида), соединенной с гальванометром, то при дви-

а б

Рис. 8.1

жении магнита гальванометр зафиксирует появление электрического тока в соленоиде и стрелка отклонится. Направление и величина отклонения стрелки и ток в соленоиде зависят от направления и скорости движения магнита. При смене полюсов магнита направление электрического тока и направление отклонения стрелки изменятся на противоположные. Электрический ток также возникнет, если перемещать соленоид относительно неподвижного магнита.

В следующей серии экспериментов Фарадей установил, что при любом из возможных вариантов опытов: 1) вдвигании (выдвигании) малого соленоида с током в большой соленоид, соединенный с гальванометром, 2) удалении (приближении) одного соленоида к другому, 3) размыкании (замыкании) тока в малом соленоиде, 4) изменении силы тока в нем – в обмотке большого соленоида возникает ток, наличие которого фиксирует гальванометр. Таким образом, было открыто явление электромагнитной индукции – появление электрического тока (названного индукционным) в замкнутом проводящем контуре при любом изменении магнитного потока, сцепленного с этим контуром. Возникновение индукционного тока свидетельствует о наличии в цепи ЭДС, называемой ЭДС электромагнитной индукции .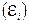

Фарадей установил, что величина индукционного тока (а значит, и ЭДС индукции) однозначно определяются скоростью изменения магнитного потока. Эта зависимость отражена в законе электромагнитной индукции Фарадея, выведенном Максвеллом: ЭДС электромагнитной индукции численно равна взятой с обратным знаком скорости изменения магнитного потока, сцепленного с рассматриваемым контуром,

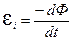. (8.1)

Знак «–» в формуле (8.1) является математическим выражением правила Ленца: индукционный ток в контуре всегда имеет такое направление, при котором создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего этот индукционный ток.

Закон Фарадея можно получить из закона сохранения энергии. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное проводнику, и может свободно перемещаться. Работа по перемещению проводника – 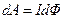, где 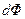– пересеченный проводником магнитный поток. Если полное сопротивление контура R, то согласно закону сохранения энергии работа источника тока за время 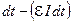будет складываться из работы, пошедшей на джоулеву теплоту 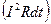, и работы по перемещению проводника в магнитном поле 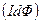, т.е. 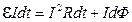, откуда 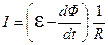, где 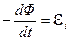и есть ЭДС электромагнитной индукции согласно закону Фарадея.

ЭДС электромагнитной индукции (как и любая ЭДС) должна иметь размерность 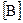. Проверим это. Согласно уравнению (8.1):

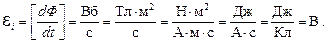
В качестве примера наиболее широкого практического применения явления электромагнитной индукции рассмотрим принцип действия генератора переменного тока (устройство для преобразования механической энергии в электрическую) на примере плоской рамки, равномерно вращающейся в однородном магнитном поле В = const c угловой скоростью w = const.

Магнитный поток, сцепленный с рамкой площадью S в любой момент времени t,равен 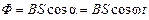, где 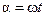– угол поворота рамки в момент времени t (начало отсчета выбрано так, что при t = 0, a = 0). При вращении в рамке будет возникать согласно закону Фарадея переменная ЭДС индукции 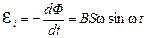, изменяющаяся со временем по гармоническому закону. При sinwt = 1, 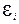– максимальна, т.е. 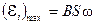. Таким образом, если в однородном магнитном поле равномерно вращается рамка, то в ней возникает переменная ЭДС, изменяющаяся по гармоническому закону 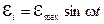. 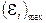, а значит, и 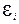прямо зависят от величин B, S, w. В России используется стандартная промышленная частота переменного тока w.

Для увеличения 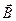применяют мощные постоянные магниты или в электромагнитах пропускают значительный ток, а также внутрь электромагнита помещают сердечник из материалов с большой магнитной проницаемостью m. Если вращать не один, а несколько витков, соединенных последовательно, то тем самым увеличивается S.

Процесс превращения механической энергии в электрическую обратим. Если через рамку, помещенную в магнитное поле, пропустить электрический ток, то на нее будет действовать вращающий момент и рамка начнет вращаться. На этом принципе основана работа электродвигателя, предназначенного для превращения электрической энергии в механическую.

Индуктивность контура. Самоиндукция

По закону Био–Савара–Лапласа индукция магнитного поля пропорциональна току, текущему в контуре, т.е. В ~ I. Магнитный поток пропорционален магнитной индукции, а значит, и току в контуре:

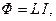(8.2)

где коэффициент пропорциональности L называется индуктивностью контура. Тогда 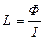и при I = 1 А, L = Ф, т.е. индуктивность контура определяется величиной магнитного потока, сцепленного с контуром, в котором течет единичный ток. Единица индуктивности в СИ – 1 Генри [1 Гн = 1 Вб/1 А].

Индуктивность контура зависит от геометрической формы контура, его размеров и магнитных свойств среды, в которой он находится. В этом смысле индуктивность контура – аналог электроемкости уединенного проводника.

Проиллюстрируем это на примере соленоида. Полный магнитный поток через соленоид

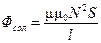. (8.3)

Если текущий в контуре ток изменяется, будет меняться и сцепленный с ним магнитный ток, а значит, в контуре будет индуцироваться ЭДС, которая в этом случае называется ЭДС самоиндукции 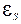, а явление ее возникновения называют самоиндукцией. Применяя к этому явлению закон Фарадея (8.1) и учитывая, что в большинстве реальных ситуаций контур не деформируется и магнитная проницаемость среды не меняется, получим выражение для ЭДС самоиндукции (при условии L = const):

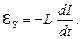(8.4)

Отсюда при 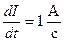, 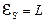и индуктивность L контура численно равна индуцированной в нем ЭДС самоиндукции при условии равенства скорости изменения тока в нем 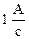. Размерность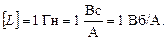

Выражение (8.4) хорошо иллюстрирует гибкость и вариативность проявления действия правила Ленца. Так, при возрастании тока в контуре 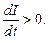Согласно уравнению (8.4) 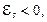т.е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и тормозит его возрастание. В обратной ситуации при убывании тока в контуре (т.е. 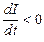) согласно выражению (8.4) 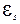> 0, т.е. индуцированный ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание. Таким образом, контур, обладая определенной индуктивностью, приобретает электрическую инертность, заключающуюся в том, что любые изменения тока тормозятся тем сильнее, чем больше индуктивность контура. Можно сказать, что роль индуктивности в электрических цепях аналогична роли массы в механике, т.е. индуктивность является мерой электрической инертности.

В качестве примера рассмотрим выключение тока в цепи, содержащей источник тока с ЭДС 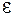, резистор сопротивлением R и катушку индуктивностью L. Под действием внешней ЭДС в цепи течет постоянный ток 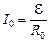(считается, что внутренним сопротивлением источника можно пренебречь). При t = 0 происходит отключение источника тока, ток начинает уменьшаться, и появляется ЭДС самоиндукции 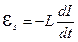. Мгновенное значение тока (по закону Ома) 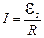или 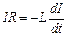. Разделив переменные и проинтегрировав правую и левую часть этого уравнения по I (от I₀ до I) и по t (от 0 до t), получим 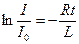или

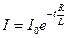. (8.5)

Таким образом, при отключении ЭДС сила тока в цепи убывает по экспоненциальному закону (8.5). Чем больше индуктивность цепи и меньше ее сопротивление, тем медленнее уменьшается ток в цепи при ее размыкании. Оценим значение ЭДС самоиндукции 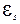, возникающей при размыкании цепи постоянного тока, т.е. при мгновенном увеличении сопротивления цепи от R₀ до 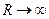. Если цепь разомкнуть при установившемся токе 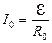, то далее ток изменяется в соответствии с уравнением (8.5) 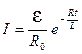и при этом текущая ЭДС самоиндукции равна

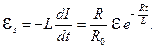(8.6)

Таким образом, при размыкании цепи и значительном увеличении сопротивления цепи 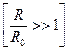, обладающей большой индуктивностью, ЭДС самоиндукции во много раз превышает ЭДС источника тока, включенного в цепь (из уравнения (8.6) получаем 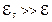). Отсюда вытекает, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (благодаря возникновению значительной ЭДС самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контуре сопротивление выводить постепенно, используя мощные «пусковые» реостаты, то ЭДС самоиндукции не достигнет больших значений. Аналогичное мероприятие необходимо осуществлять и при замыкании цепи постоянного тока.