Устойчивость оболочки при внешнем давлении

Если оболочка очень длинная, то влиянием условий закрепления ее торцов на величину критического давления можно пренебречь. Это означает, что оболочка может деформироваться без удлинений и сдвигов срединной поверхности. Тогда каждое поперечное сечение будет вести себя как кольцо. Следовательно, можно воспользоваться решением для кольца, положив его толщину равной толщине оболочки, а ширину - единичной.

Тогда 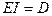и формула (19.23) даст

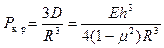(20.16)

или

.

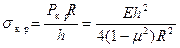Форма потери устойчивости нерастяжимой оболочки описывается собственными функциями

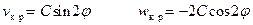. (20.17)

Отметим, что так может потерять устойчивость и не слишком длинная оболочка при условии, что ее торцы свободны от закрепления.

Для оболочки с закрепленными торцами следует решать задачу на собственные значения (20.14),(20.15), положив .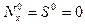

Решение этой задачи всегда можно строить в одинарных рядах

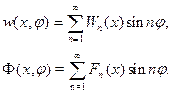(20.18)

В этом случае мы придем к системе или одному уравнению с постоянными коэффициентами по координате 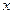и далее - к системе восьми трансцендентных уравнений относительно 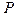, выражающих граничные условия. Решение такой системы возможно только с помощью ЭВМ, а ее качественный анализ практически невозможен.

Лишь при одном варианте граничных условий решение оказывается простым. Это условия, допускающие решение в двойных тригонометрических рядах

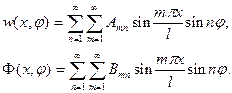(20.19)

Представление (29.19) отвечает условиям на торцах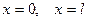

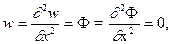(20.20)

причем условия по 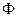означают

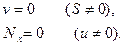
Эти условия можно представить себе так: нерастяжимый торец оболочки шарнирно скреплен со шпангоутом, абсолютно жестким в своей плоскости и абсолютно гибким из нее.

Вследствие ортогональности тригонометрических функций в (29.19) уравнения (20.14) распадутся на независимые

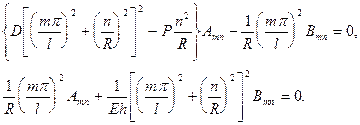(20.21)

Приравнивая нулю определитель системы (20.21), получаем

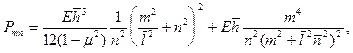(20.22)

где введены безразмерные параметры

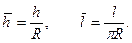
Очевидно, что 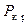будет получаться из (20.22) при 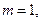что соответствует одной полуволне в продольном направлении,

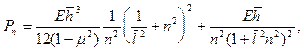(20.23)

а значение 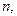дающее 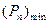, будет зависеть от сочетания параметров 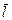и .

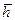Для качественного анализа удобно ввести безразмерное критическое давление

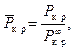
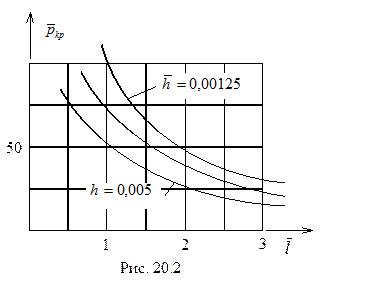
где 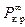- определяется формулой (20.16).

Напомним, что уравнения (20.14) и, следовательно, формула (20.23) получены для упрощенных соотношений (20.2),(20.3). Поэтому при 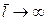величина 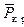не стремится к единице.

Если же не упрощать соотношения (20.2),(20.3), и решать задачу в перемещениях, то мы получим вместо (20.23) более громоздкую, однако более точную формулу

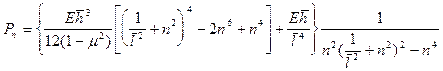. (20.24)

Эта формула при 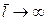обращается в (20.16). Анализ показывает, что формулой (20.24) можно пользоваться при 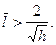Такие оболочки принято называть длинными.

Для оболочек средней длины 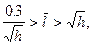как показывают вычисления, можно принять 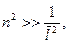и тогда формулы (20.23), (20.24) принимают вид

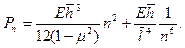
Поскольку 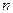достаточно велико, зависимость 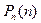можно считать непрерывной и, дифференцируя 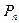по 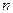из условия 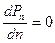найти (при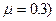

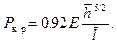(20.25)

Это формула Папковича. В безразмерном виде она выглядит так

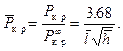
Для коротких оболочек 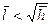формула (20.24) также упрощается. В этом случае 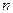оказывается настолько велико, что в формуле (20.23) можно опустить второй член. Тогда

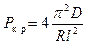(20.26)

вызывает потерю устойчивости с образованием 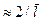полуволн.

Приведенные результаты справедливы, строго говоря, только для граничных условий (20.20). Однако исследования показывают, что ими можно пользоваться и при других условиях на торцах оболочки. Исключение составляют такие варианты закрепления торцов, которые в конструкциях не реализуются.

С другой стороны, нагружение реальных оболочек внешним давлением практически всегда сопровождается их сжатием или растяжением. Например, при всестороннем сжатии цилиндрической оболочки с днищами

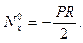
Это сжатие можно учесть, добавив к 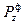величину 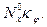Результаты показывают, что влияние осевых усилий 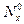, соизмеримых с 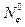, существенно лишь для очень коротких оболочек, которые можно рассчитать по формулам типа (20.26) как пластины.

Иная картина возникает, когда 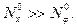Такую задачу называют задачей устойчивости при осевом сжатии.