Лекция 14. Неравномерность хода машины при установившемся движении.
Вопросы, рассматриваемые на лекции. Балансировка роторов. Уравновешивание сил с помощью противовесов и разгружающих устройств. Исследование установившегося движения по диаграмме энергомасс.
Некоторые основные понятия.
Ротором в теории балансировки называют любое звено механизма, совершающее вращательное движение. Балансировка роторов приобрела особое значение в связи с повышением частоты вращения звеньев, приводящим к резкому увеличению сил и моментов сил инерции от неуравновешенных масс. Уравновешивание действия сил инерции и моментов сил инерции вращающихся звеньев относится к наиболее актуальным задачам современного машиностроения.
Для полного устранения динамических нагрузок на опоры ротора, главный вектор сил инерции и момент сил инерции должны быть равны нулю в любой момент движения: Ри=0, Ми=0.
Решение задачи уравновешивания вращающихся деталей заключается в подборе их масс, обеспечивающем полное или частичное гашение добавочных инерционных нагрузок на опоры.
Из механики известно, что свободно вращающееся тело не оказывает динамических воздействий на опоры в том случае, когда центр тяжести тела лежит на геометрической оси вращения и ось вращения является главной центральной осью инерции. Выполнение первого условия называют статической балансировкой, выполнение обоих условий- динамической балансировкой.
Сбалансированное звено будет находиться в состоянии равновесия при повороте вокруг оси на любой угол.
Практика уравновешивания идет по пути динамической балансировки всей вращающейся системы в целом с помощью двух противовесов. При этом одновременно выполняются условия статической и динамической уравновешенности.
Пусть имеется ротор с пятью плоскостями, перпендикулярными к оси вращения (рис.38). Во всех пяти плоскостях сделаны радиальные прорези, в которых могут быть установлены определенные массы. Прорези необходимы для изменения положения массы относительно оси вращения. Плоскости могут поворачиваться вокруг оси вращения, изменяя углы 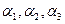 . Допустим, в плоскостях I,II,III установлены неуравновешенные массы m1, m2, m3. Положения неуравновешенных масс в плоскостях заданы радиус-векторами r1,r2,r3 . Углы смещения этих масс относительно произвольно выбранной оси соответственно
. Допустим, в плоскостях I,II,III установлены неуравновешенные массы m1, m2, m3. Положения неуравновешенных масс в плоскостях заданы радиус-векторами r1,r2,r3 . Углы смещения этих масс относительно произвольно выбранной оси соответственно 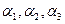 . Крайние плоскости А и В, располагающиеся по возможности ближе к опорам, считаются плоскостями приведения (коррекции). Положения плоскостей I,II и III относительно плоскости приведения А определяется соответственно координатами z1, z2, z3. Противовесы устанавливаются в плоскостях А и В, расстояние между ними L.
. Крайние плоскости А и В, располагающиеся по возможности ближе к опорам, считаются плоскостями приведения (коррекции). Положения плоскостей I,II и III относительно плоскости приведения А определяется соответственно координатами z1, z2, z3. Противовесы устанавливаются в плоскостях А и В, расстояние между ними L.
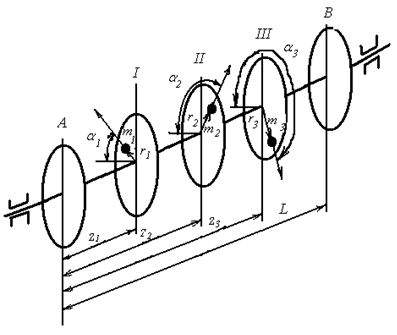
Рис.38
Для оценки неуравновешенности вводится понятие дисбаланса. Дисбаланс-векторная величина, равная произведению неуравновешенной массы на ее эксцентриситет относительно оси ротора.
Приведем к плоскостям А и В дисбалансы D1=m1r1, D2=m2r2, D3=m3r3 всех неуравновешенных масс, то есть заменим каждый вектор дисбаланса двумя параллельными ему и расположенными в плоскостях приведения по закону расположения параллельных сил:
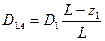
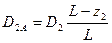
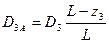 (17)
(17)
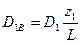
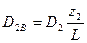
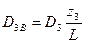
В результате в каждой плоскости приведения имеем по три вектора дисбаланса (рис.39). Для компенсации дисбаланса необходимо построить силовой многоугольник согласно уравнениям:
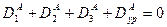 (18)
(18)
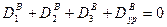
где DурА ,DурВ- уравновешивающие дисбалансы в плоскостях А и В.
Из многоугольников, изображенных на рис.40, находят DурА и DурВ, затем задаваясь уравновешивающими массами mурА и mурВ, определяют радиусы rурА и rурВ. Углы, под которыми должны быть расположены векторы DурА и DурВ в плоскостях А и В, также определяют из построения силовых многоугольников (рис.40).
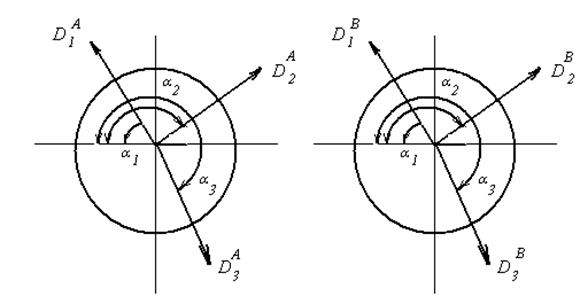 |
Рис.39

Рис.40
Диаграмма энергомасс строится исключением параметра 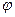 из графиков
из графиков 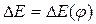 и
и 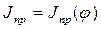 . К полученной диаграмме проводятся касательные под углами
. К полученной диаграмме проводятся касательные под углами 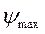 и
и 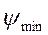 .
.
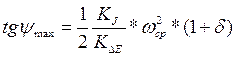 ,
,
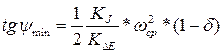 ,
,
где wср= wкр
d- коэффициент неравномерности
Касательные отсекают на вертикали отрезок kl, тогда момент инерции маховика может быть рассчитан по формуле:
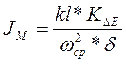 ,
, 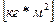
Если 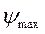 и
и 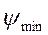 имеют значения близкие к 90о, то касательные пересекут вертикаль далеко за пределами чертежа. Поэтому отрезок kl определяют аналитически следующим образом.
имеют значения близкие к 90о, то касательные пересекут вертикаль далеко за пределами чертежа. Поэтому отрезок kl определяют аналитически следующим образом.
Из треугольника Domk (рис.41) следует:
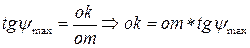
Из треугольника Donl следует:
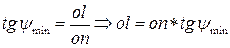
(длины om и on [мм] определяют по диаграмме).
Тогда kl=ol-ok [мм]
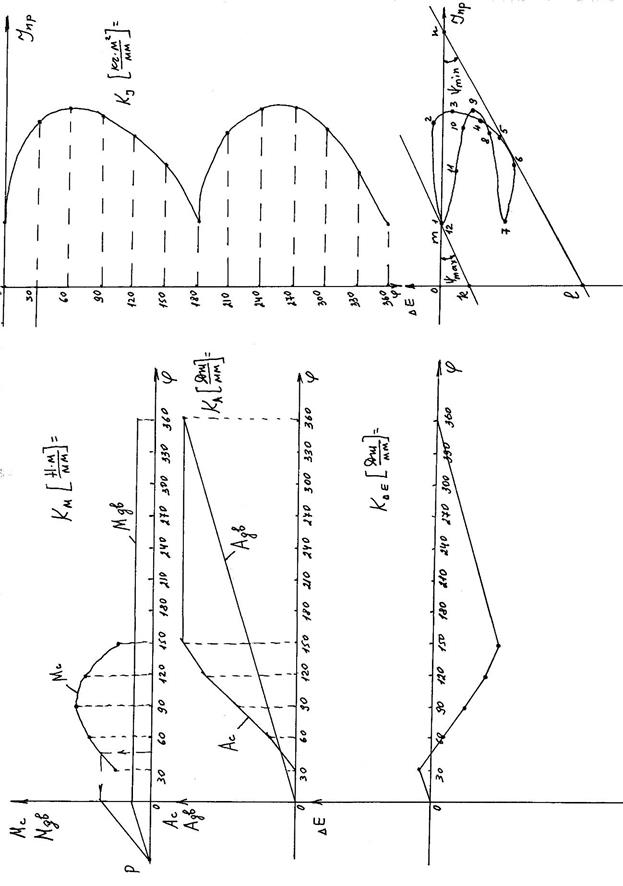
Рис.41
Дата добавления: 2020-12-11; просмотров: 613;











