Решение алгебраических уравнений
Из алгебраических уравнений вида 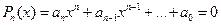 мы научились решать в школе линейные уравнения вида
мы научились решать в школе линейные уравнения вида 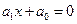 и квадратные уравнения
и квадратные уравнения 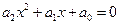 . В обоих случаях коэффициент при старшей степени не должен равняться 0. Мы знаем, что даже квадратное уравнение не всегда имеет корни на множестве действительных чисел. В приложениях, связанных с комплексными числами, очень важно находить корни многочлена от комплексной переменной.
. В обоих случаях коэффициент при старшей степени не должен равняться 0. Мы знаем, что даже квадратное уравнение не всегда имеет корни на множестве действительных чисел. В приложениях, связанных с комплексными числами, очень важно находить корни многочлена от комплексной переменной.
В отличии от этого, алгебраическое уравнение с комплексной переменной 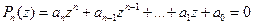 степени выше нулевой всегда имеет хотя бы один, вообще говоря, комплексный корень. В этом суть «основной теоремы алгебры», которую мы сформулируем без доказательства.
степени выше нулевой всегда имеет хотя бы один, вообще говоря, комплексный корень. В этом суть «основной теоремы алгебры», которую мы сформулируем без доказательства.
Теорема 1. (Основная теорема алгебры) При 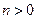 уравнение
уравнение 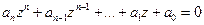 имеет хотя один, один, вообще говоря, комплексный корень.
имеет хотя один, один, вообще говоря, комплексный корень.
А вот теорема Безу легко доказывается.
Теорема 2. (Теорема Безу) Остаток от деления 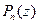 на двучлен
на двучлен 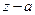 равен
равен 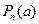 .
.
Доказательство. Пусть 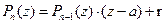 , тогда
, тогда 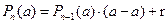 , откуда
, откуда 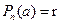 .
.
Следствие 1. Многочлен 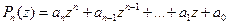 разлагается на
разлагается на 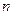 линейных множителей, т.е. представляется в виде
линейных множителей, т.е. представляется в виде 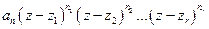 , где
, где 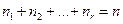 .
.
Пример 4. Решите уравнение 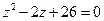 .
.
Решение. Применим формулу для решения квадратного уравнения с четным коэффициентом при линейном члене. Итак, 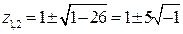 . Под
. Под 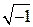 здесь понимается любое число, квадрат которого равен
здесь понимается любое число, квадрат которого равен 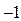 . Таким числом может быть число
. Таким числом может быть число 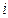 , и в итоге
, и в итоге 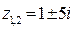 .
.
Ответ. 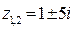 .
.
Пример 5. Решите уравнение 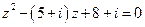 .
.
Решение. Применим формулу для решения квадратного уравнения с четным коэффициентом при линейном члене. Итак, 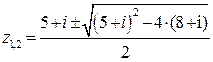 или
или 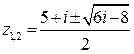 . Под
. Под 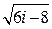 здесь понимается любое число, квадрат которого равен
здесь понимается любое число, квадрат которого равен 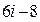 . Если число
. Если число 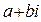 возвести в квадрат и приравнять к
возвести в квадрат и приравнять к 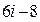 , то несложно выяснить, что одним из значений
, то несложно выяснить, что одним из значений 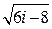 является число
является число 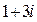 . В итоге
. В итоге 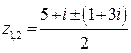 , и мы приходим к ответу
, и мы приходим к ответу 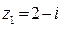 ,
, 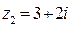 . Заметим, что можно было «подобрать» эти корни, используя теорему Виета.
. Заметим, что можно было «подобрать» эти корни, используя теорему Виета.
Ответ. 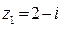 ,
, 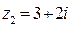 .
.
Дата добавления: 2016-09-06; просмотров: 1536;











