Теорема Кронекера - Капеллі, наслідки з неї. Критерій сумісності СЛАР

Система лінійних рівнянь сумісна тоді й лише тоді, коли ранг r основної матриці системи дорівнює рангу 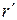розширеної матриці цієї системи.

За цією теоремою, якщо ранги основної та розширеної матриць не рівні, то система несумісна й немає сенсу її розв’язувати. Якщо ранги матриць рівні, то система сумісна.

Для сумісних лінійних рівнянь можливі такі випадки.

1. Якщо ранг матриці сумісної системи дорівнює числу невідомих, тобто r=n, то система (1) має єдиний розв’язок.

2. Якщо ранг матриці сумісної системи менший від числа невідомих, тобто 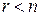, то система невизначена й має нескінченну кількість розв’язків.

Нехай 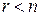; тоді r невідомих x₁, x₂, ¼, x_r називаються основними, або базисними, якщо визначник матриці з коефіцієнтів при цих невідомих відмінний від нуля. Решта n-r невідомих називаються неосновними, або вільними. Оскільки вільні невідомі можуть набувати довільних значень, то в цьому разі система буде невизначеною.

Розв’язок (1), в якому всі n-r неосновних невідомих дорівнюють нулю, називають базисним.