Индуктивное сопротивление - это прирост лобового сопротивления, связанный с образованием подъемной силы крыла.
При обтекании крыла воздушным потоком возникает разность давлений над крылом и под ним. В результате часть воздуха на концах крыла перетекает из зоны большего давления в зону меньшего давления (Рис. 3.17).
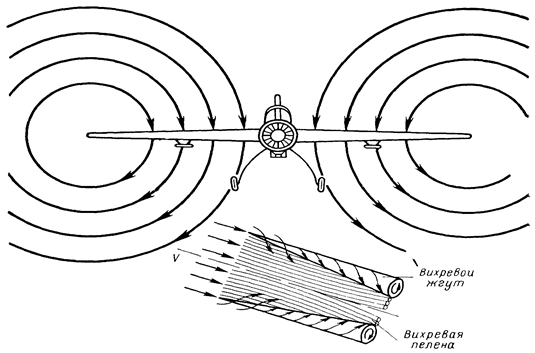
Рис. 3.17 Обтекание крыла конечного размаха
Поток воздуха перетекает с нижней поверхности крыла на верхнюю и накладывается на воздушный поток, набегающий на верхнюю часть крыла – образуется вихревой жгут.
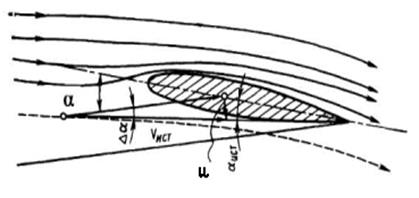
Рис. 3.18 Отклонение воздушного потока вниз, вызванное вихревым жгутом
Вращающийся воздух в жгуте увлекает за собой окружающий воздух.
Такое движение воздушных масс сообщает воздушному потоку дополнительную скорость, направленную вниз. При этом воздух, обтекающий крыло со скоростью V, отклоняется вниз со скоростью U( Рис. 3.18).
Угол Da, на который отклоняется поток воздуха, называется углом скоса потока. Величина его зависит от значения вертикальной скорости, индуцированной вихревым жгутом, и истинной скорости набегающего потока Vист:

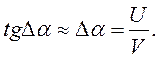
Благодаря скосу потока истинный угол атаки aист крыла будет отличаться от геометрического угла атаки a на величину Da (Рис. 3.19):
Рис. 3.19 Образование индуктивного сопротивления
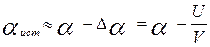 .
.
Поворот набегающего потока вызывает поворот назад на угол 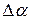 вектора истинной подъемной силы. Согласно теореме Н.Е. Жуковского, она должна быть перпендикулярна к истинной скорости потока.
вектора истинной подъемной силы. Согласно теореме Н.Е. Жуковского, она должна быть перпендикулярна к истинной скорости потока.
Подъемной силой будет не вся сила Y' а ее составляющая Y, направленная перпендикулярно набегающему потоку:
Вторая составляющая истинной подъемной силы равна: 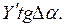 Она действует в направлении невозмущенного потока в сторону, противоположную движению, и является силой индуктивного сопротивления
Она действует в направлении невозмущенного потока в сторону, противоположную движению, и является силой индуктивного сопротивления 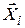 .
.
Следовательно, индуктивное сопротивление – это проекция истинной подъемной силы на направление движения крыла.
Чем больше угол скоса потока 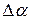 , тем сильнее отклоняется назад подъемная сила
, тем сильнее отклоняется назад подъемная сила 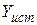 , и тем больше индуктивное сопротивление
, и тем больше индуктивное сопротивление 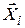 .
.
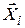 определяется по общим аэродинамическим формулам:
определяется по общим аэродинамическим формулам:
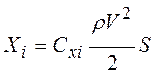 ,
,
где Cxi- коэффициент индуктивного сопротивления.
Формула для его расчета выведена теоретическим путем:
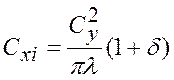 .
.
Из формулы видно, чтоСхiпропорционален квадрату коэффициента подъемной силы и обратно пропорционален удлинению крыла. Коэффициент δ учитывает форму крыла в плане. Для прямоугольного крыла 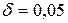 , для эллиптического
, для эллиптического 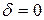 .
.
Из формулы следует, что минимальным индуктивным сопротивлением обладают эллиптические крылья, максимальным – прямоугольные.
При увеличении углов атаки индуктивное сопротивление возрастает в квадрате. При увеличении удлинения 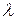 индуктивное сопротивление снижается. Во многих случаях полета, особенно при полете с дозвуковой скоростью на больших высотах, индуктивное сопротивление составляет значительную часть сопротивления крыла. Поэтому самолеты, предназначенные для полетов на большие расстояния, имеют крылья большого удлинения. Индуктивное сопротивление снижается также за счет применения геометрической и аэродинамической крутки крыла.
индуктивное сопротивление снижается. Во многих случаях полета, особенно при полете с дозвуковой скоростью на больших высотах, индуктивное сопротивление составляет значительную часть сопротивления крыла. Поэтому самолеты, предназначенные для полетов на большие расстояния, имеют крылья большого удлинения. Индуктивное сопротивление снижается также за счет применения геометрической и аэродинамической крутки крыла.
Вывод: Разность давлений на поверхности крыла определяет величину подъемной силы, поэтому между подъемной силой и индуктивным сопротивлением имеется связь. Если нет подъемной силы, индуктивное сопротивление отсутствует.
Чем больше угол атаки, тем больше подъемная сила и, следовательно, индуктивное сопротивление увеличивается.
При угле атаки нулевой подъемной силы α0 концевых вихрей нет, поэтому 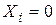 . На углах атаки, отличающихся от α0, сопротивление крыла состоит из профильного сопротивления и индуктивного:
. На углах атаки, отличающихся от α0, сопротивление крыла состоит из профильного сопротивления и индуктивного:
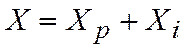 ;
; 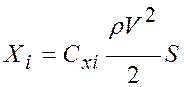 ,
,
где СХi – коэффициент индуктивного сопротивления.
Переходя от сил к их коэффициентам, получим формулу коэффициента лобового сопротивления профиля крыла: 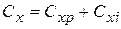 .
.
Зависимость Cx от угла атаки является важной аэродинамической характеристикой крыла.
Зависимость коэффициента лобового сопротивления от угла атаки. Эта зависимость строится после продувок модели крыла в аэродинамической трубе (рис. 3.20) с помощью формулы Сx = 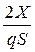 , где Сx- коэффициент лобового сопротивления профиля крыла;
, где Сx- коэффициент лобового сопротивления профиля крыла;
X -сила лобового сопротивления модели крыла; 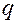 - скоростной напор воздушного потока в аэродинамической трубе; S – площадь крыла модели.
- скоростной напор воздушного потока в аэродинамической трубе; S – площадь крыла модели.

Рис. 3.20 Зависимость СХ = 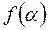
График представляет собой квадратную параболу, каждая точка которой найдена суммированием двух коэффициентов – профильного сопротивления Сxр и индуктивного Сxi:
Сx = Сxр + Сxi.
График показывает, что коэффициент Сx на любом угле атаки не равен нулю, так как обтекание профиля без сопротивления невозможно.
На малых углах атаки коэффициент Сx имеет минимальное значение и соответствует профильному сопротивлению.
С увеличением углов атаки Сxр почти не изменяется, а индуктивное быстро растет (пропорционально Сy2). По мере приближения к критическому углу атаки рост Сx ускоряется из-за начинающегося срыва потока.
Графическая зависимость 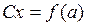 позволяет также определить влияние кривизны профиля. Для несимметричных профилей (кривая 2) график смещается влево. Это означает, что Сx у несимметричного профиля больше, чем у симметричного (кривая 1).
позволяет также определить влияние кривизны профиля. Для несимметричных профилей (кривая 2) график смещается влево. Это означает, что Сx у несимметричного профиля больше, чем у симметричного (кривая 1).
Вывод: Известно, что чем меньше углы атаки, тем больше скорость полета. Поэтому на больших скоростях полета наибольшая доля сопротивления приходится на профильное сопротивление. Поэтому на сопротивление основное влияние оказывают толщина и кривизна профиля, состояние поверхности крыла.
На малых скоростях полета и больших углах атаки основная доля в общем сопротивлении крыла – это индуктивное сопротивление. Поэтому основное внимание уделяется размерам площади и удлинения крыла.
Дата добавления: 2016-09-06; просмотров: 15260;











