Обратное преобразование Лапласа

Для вычисления обратного преобразования Лапласа напомним соотношение (1.2-5)

. (1.2-5)

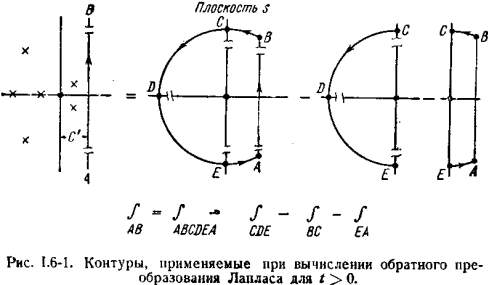
Интегрирование здесь выполняется вдоль линии s=c, параллельной мнимой оси и смещенной так, что все особенности F(s) лежат с левой стороны от нее. С помощью приема, подобного тому, который использовался для обратного преобразования Фурье, интеграл (1.2-5) представляется суммой интеграла по замкнутому контуру и трех интегралов по линиям, как показано на рис. 1.6-1,

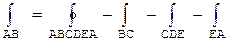. (1.6-1)

Если поведение F(s)при очень больших s таково, что

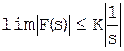, (1.6-2)

и если t положительно, можно показать, как и для преобразования Фурье, что значение интеграла вдоль линии CDE — замыкающей окружности большого радиуса — стремится к нулю, когда радиус становится бесконечно большим. Можно показать, что интегралы no сегментам ВС и ЕА стремятся к нулю при бесконечном радиусе.

Следовательно (поскольку все свелось к интегралу по замкнутому контуру), обратное преобразование Лапласа можно вычислить непосредственно по вычетам в полюсах F(s) 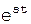в конечной части s-плоскости

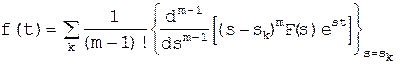(1.6-15)

В качестве примера использования этого выражения возьмем (1.5-14) и будем считать его преобразованием Лапласа

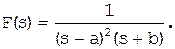(1.6-16)

Мы хотим найти оригинал. Вначале определяются вычеты F(s) 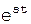в полюсах а и —b

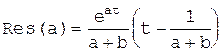, (1.6-17)

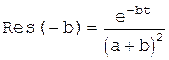. (1.6-18)

Тогда функция f(t) будет иметь следующий вид:

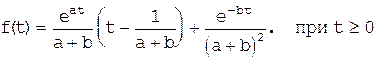(1.6-19)

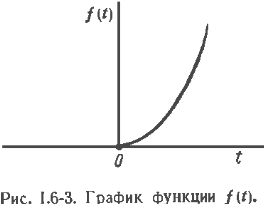
График этой функции показан на рис. 1.6-3 и, как это видно, значительно отличается от функции, полученной в соответствии с (1.6-16), когда (1.6-16) полагалось преобразованием Фурье. Согласно приведенным результатам, а также свойству единственности преобразований, можно заключить, что если преобразование имеет полюсы как в левой, так и в правой полуплоскости, то обратные преобразования Фурье и Лапласа будут с необходимостью различными. Однако если полюсы преобразования лежат только в левой полуплоскости, то обратные преобразования Фурье и Лапласа идентичны.