Лекция 7. Альфа-распад

7.1. Феноменологическое рассмотрение. Альфа-распадом называется самопроизвольный процесс превращения ядра (А, Z) в ядро (A – 4, Z – 2) с испусканием ядра гелия-4 (α-частицы):

.

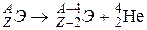Согласно условию (5.1), такой процесс возможен, если энергия α-распада

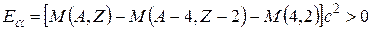. (7.1)

Выражая энергию покоя ядра через сумму энергий покоя нуклонов и энергию связи ядра, перепишем неравенство (7.1) в следующем виде:

,

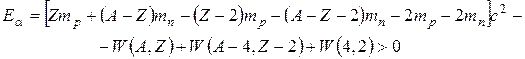или

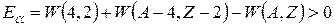(7.2)

Результат (7.2), в который входят лишь энергии связи ядер, обусловлен тем, что при α-распаде сохраняется не только общее число нуклонов, но и число протонов и нейтронов в отдельности.

Рассмотрим, как меняется энергия α-распада Е_α при изменении массового числа A. Используя формулу Вайцзеккера для ядер, лежащих на теоретической линии стабильности, можно получить зависимость, представленную на рис. 7.1. Видно, что в рамках капельной модели α-распад должен наблюдаться для ядер с A > 155, причем энергия распада будет монотонно увеличиваться с ростом A.

На том же рисунке изображена реальная зависимость Е_α от A, построенная с использованием экспериментальных данных об энергиях связи. Сравнивая две кривые, можно видеть, что капельная модель передает лишь общую тенденцию изменения Е_α. В действительности самым легким радионуклидом, испускающим α-частицы, является ¹⁴⁴Nd, т.е. реальная область α-радиоактивности несколько шире, чем предсказывает полуэмпирическая формула. Кроме того, зависимость энергии распада от A не монотонна, а имеет максимумы и минимумы. Наиболее ярко выраженные максимумы приходятся на области A = 140-150 (редкоземельные элементы) и A = 210-220. Появление максимумов связано с заполнением нейтронной и протонной оболочек дочернего ядра до магического числа: N = 82 и Z = 82. Как известно, заполненным оболочкам соответствуют аномально высокие энергии связи. Тогда, согласно модели нуклонных оболочек, энергия α-распада ядер с N или Z, равным 84 = 82 + 2, будет также аномально высока. Благодаря оболочечному эффекту область α-радиоактивности начинается с 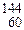Nd (N = 84), а у подавляющего большинства α-активных ядер Z 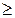84.

Увеличение числа протонов в ядре (при постоянном A) способствует α-распаду, т.к. увеличивает относительную роль кулоновского отталкивания, дестабилизирующего ядро. Поэтому энергия α-распада в ряду изобаров будет увеличиваться с ростом числа протонов. Увеличение числа нейтронов действует противоположным образом.

Для ядер, перегруженных протонами, конкурирующими процессами могут стать β⁺-распад или электронный захват, т.е. процессы, приводящие к уменьшению Z. Для ядер с избытком нейтронов конкурирующим процессом является β^–-распад. Начиная с массового числа A = 232, к перечисленным типам распада добавляется спонтанное деление. Конкурирующие процессы могут идти настолько быстро, что наблюдать α-распад на их фоне не всегда удается.

Рассмотрим теперь, как распределяется энергия распада между фрагментами, т.е. α-частицей и дочерним ядром, или ядром отдачи. Очевидно, что

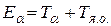, (7.3)

где Т_α – кинетическая энергия α-частицы, Т_я.о. – кинетическая энергия дочернего ядра (энергия отдачи). Согласно закону сохранения импульса (который в состоянии до распада равен нулю[54]), образовавшиеся частицы получают импульсы, равные по абсолютной величине и противоположные по знаку:

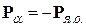. (7.4)

Воспользуемся далее рис. 7.1, из которого следует, что энергия α-распада (а значит, и кинетическая энергия каждой из частиц) не превышает 10 МэВ. Энергия покоя α-частицы – около 4 ГэВ, т.е. в сотни раз больше. Еще больше энергия покоя дочернего ядра. В этом случае для установления связи кинетической энергии с импульсом можно использовать соотношение классической механики

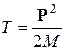. (7.5)

При подстановке (7.5) в (7.3) получаем

,

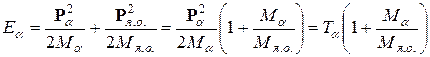или

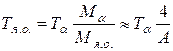. (7.6)

Из (7.6) следует, что основную часть энергии распада уносит наиболее легкий фрагмент – α-частица. Так, при A = 200 на дочернее ядро отдачи приходится всего лишь 2 % от Е_α.[55]

Однозначное распределение энергии распада между двумя фрагментами приводит к тому, что каждый радионуклид испускает альфа-частицы строго определенных энергий, или, иными словами, α-спектры являются дискретными. Благодаря этому по энергии α-частиц можно идентифицировать радионуклид: линии спектра служат своеобразными «отпечатками пальцев». При этом, как показывает эксперимент, в α-спектрах очень часто присутствует не одна, а несколько линий различной интенсивности с близкой энергией. В таких случаях говорят о тонкой структуре α-спектра (рис. 7.2).

Чтобы понять происхождение эффекта тонкой структуры, вспомним, что энергия α-распада есть не что иное, как разность между уровнями энергии материнского и дочернего ядра. Если бы переход совершался лишь из основного состояния материнского ядра в основное состояние дочернего, α-спектры всех радионуклидов содержали бы только по одной линии. Между тем оказывается, что переходы из основного состояния материнского ядра могут происходить и в возбужденные состояния.

Периоды полураспада α-излучателей изменяются в широких пределах: от 10^–7 секунды до 10¹⁷ лет. Напротив, энергия испускаемых α-частиц лежит в узком диапазоне: 1-10 МэВ. Связь между постоянной распада λ и энергией α-частиц Т_α дается законом Гейгера–Неттола, одна из форм записи которого:

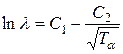, (7.7)

где С₁ и С₂ – константы, мало изменяющиеся при переходе от ядра к ядру. При этом увеличению энергии α-частиц на 1 МэВ соответствует уменьшение периода полураспада на несколько порядков величины.

7.2. Прохождение α-частиц через потенциальный барьер.До появления квантовой механики не было дано теоретического объяснения столь резкой зависимости λ от Т_α. Более того, загадочной казалась сама возможность вылета из ядра α-частиц с энергиями, значительно уступающими высоте потенциальных барьеров, которые, как было доказано, окружают ядра. Например, опыты по рассеянию α-частиц ²¹²Ро с энергией 8,78 МэВ на уране показывали, что вблизи ядра урана не наблюдается отклонений от закона Кулона; тем не менее уран испускает α-частицы с энергией всего лишь 4,2 МэВ. Каким же образом эти α-частицы проникают через барьер, высота которого, как минимум, 8,78 МэВ, а в действительности еще больше?..

На рис. 7.3 изображена зависимость потенциальной энергии U положительно заряженной частицы от расстояния до ядра. В области r > R между частицей и ядром действуют только силы электростатического отталкивания, в области r < R преобладают более интенсивные ядерные силы притяжения, препятствующие вылету частицы из ядра. Результирующая кривая U(r) имеет острый максимум в области r ~ R, получивший название кулоновского потенциального барьера. Высота барьера

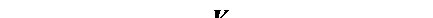
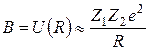, (7.8)

где Z₁ и Z₂ – заряды вылетающей частицы и дочернего ядра, R – радиус ядра, который в случае α-распада принимают равным 1,57·A^1/3 фм. Нетрудно подсчитать, что для ²³⁸U высота кулоновского барьера составит ~ 27 МэВ.

Вылет из ядра α-частиц (и других положительно заряженных нуклонных образований) объясняется квантовомеханическим эффектом тунелирования, т.е. возможностью частицы двигаться в классически запрещенной для нее области между точками поворота, где Т < U.

Для того чтобы найти вероятность прохождения положительно заряженной частицы через кулоновский потенциальный барьер, рассмотрим вначале прямоугольный барьер ширины a и высоты V, на который падает частица с энергией E (рис. 7.4). За пределами барьера в областях 1 и 3 уравнение Шредингера выглядит как

,

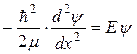а во внутренней области 2 как

.

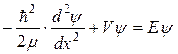Решением его являются плоские волны

,

,

,

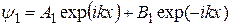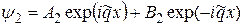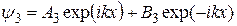причем

.

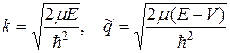Амплитуда А₁ соответствует волне, падающей на барьер, В₁ – волне, отраженной от барьера, А₃ – волне, прошедшей сквозь барьер (так как прошедшая волна уже более не отражается, амплитуда В₃ = 0). Поскольку Е < V,

величина q – чисто мнимая, и волновая функция под барьером

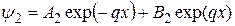, (7.9)

где

.

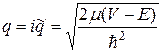Второе слагаемое в формуле (7.9) отвечает экспоненциально растущей волновой функции, а значит, и растущей с увеличением х вероятности обнаружить частицу под барьером. В связи с этим величина В₂ не может быть большой по сравнению с А₂. Тогда, положив В₂ просто равным нулю, имеем

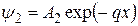. (7.10)

Коэффициент прозрачности D барьера, т.е. вероятность найти частицу, первоначально находившуюся в области 1, в области 3, есть просто отношение вероятностей обнаружить частицу в точках х = а и х = 0. Для этого достаточно знания волновой функции под барьером. В результате[56]

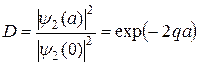. (7.11)

Представим далее потенциальный барьер произвольной формы как совокупность N прямоугольных потенциальных барьеров с высотой V(x) и шириной Δx (рис. 7.5). Вероятность прохождения частицы через такой барьер есть произведение вероятностей пройти все барьеры друг за другом, т.е.

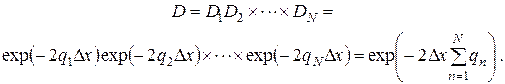
Тогда, рассматривая барьеры бесконечно малой ширины и переходя от суммирования к интегрированию, получаем

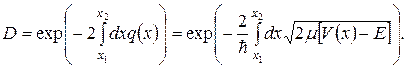(7.12)

Пределы интегрирования x₁ и x₂ в формуле (7.12) соответствуют классическим точкам поворота, в которых V(x) = E, при этом движение частицы в областях x < x₁ и x > x₂ считается свободным.

Для кулоновского потенциального барьера вычисление D согласно (7.12) можно провести точно. Это впервые было сделано Г.А. Гамовым в 1928 г., т.е. еще до открытия нейтрона (Гамов полагал, что ядро состоит из α-частиц).[57]

Для α-частицы с кинетической энергией T в потенциале вида u/r выражение для коэффициента прозрачности барьера принимает следующий вид:

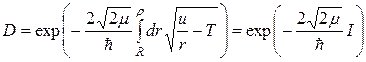, (7.13)

причем значение ρ определяется равенством T = u/ρ. Интеграл в показателе экспоненты после подстановки ξ = r^1/2 принимает форму, удобную для интегрирования:

.

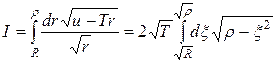Последнее дает

.

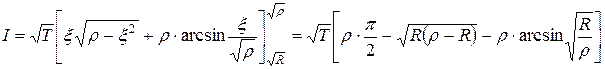Если высота кулоновского барьера значительно больше, чем энергия α-частицы, то ρ >> R. В этом случае

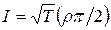. (7.14)

Подставляя (7.14) в (7.13) и учитывая, что ρ = BR/T, получаем

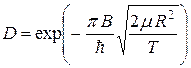. (7.15)

В общем же случае, когда высота кулоновского барьера сравнима с энергией испускаемой частицы, коэффициент прозрачности D дается следующей формулой:

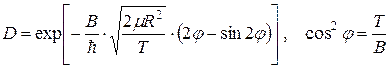, (7.16)

где 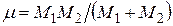– приведенная масса двух разлетающихся частиц (для α-частицы она очень близка к ее собственной массе). Формула (7.16) дает для ²³⁸U значение D = 10^–39, т.е. вероятность тунелирования α-частиц крайне мала.

Результат (7.16) был получен для случая центрального разлета частиц, т.е. такого, когда α-частица испускается ядром строго в радиальном направлении. Если же последнее не имеет места, то уносимый α-частицей момент импульса 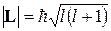не равен нулю. Тогда при расчетах D следует учитывать поправку, связанную с наличием дополнительного центробежного барьера:

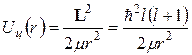, (7.17)

где l = 1, 2, 3, и т.д.

Значение U_ц(R) называется высотой центробежного барьера. Существование центробежного барьера приводит к возрастанию интеграла в (7.12) и уменьшению коэффициента прозрачности. Однако эффект центробежного барьера не слишком велик. Во-первых, поскольку вращательная энергия системы в момент разлета U_ц(R) не может превышать энергию α-распада T, то чаще всего 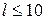, и высота центробежного барьера не превышает 25% от кулоновского. Во-вторых, следует учесть, что центробежный потенциал (~1/r²) гораздо быстрее убывает с расстоянием, чем кулоновский (~1/r). В результате вероятность испускания α-частицы с l ≠ 0 имеет практически тот же порядок величины, что и при l = 0.

Возможные значения l определяются правилами отбора по моменту импульса и четности, которые вытекают из соответствующих законов сохранения. Так как спин α-частицы равен нулю, а ее четность положительна, то

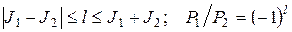(7.18)

(индексы 1 и 2 относятся к материнскому и дочернему ядру соответственно). С помощью правил (7.18) нетрудно, например, установить, что α-частицы ²³⁹Pu (рис. 7.2) с энергией 5,157 МэВ испускаются только при центральном разлете, тогда как для α-частиц с энергией 5,144 и 5,016 МэВ l = 2.

7.3. Скорость α-распада. Вероятность α-распада как сложного события – произведение двух величин: вероятности образования α-частицы внутри ядра и вероятности покинуть ядро. Процесс образования α-частицы – чисто ядерный; его довольно сложно рассчитать точно, поскольку ему присущи все трудности ядерной задачи. Тем не менее, для простейшей оценки можно принять, что α-частицы в ядре существуют, что называется, «в готовом виде». Пусть v – скорость α-частицы внутри ядра. Тогда на его поверхности она окажется n раз в единицу времени, где n = v/2R. Положим, что по порядку величины радиус ядра R равен длине волны де Бройля α-частицы (см. приложение Б), т.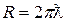е. , где 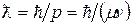. Рассматривая, таким образом, вероятность распада как произведение коэффициента прозрачности барьера и частоты соударений α-частицы с барьером, имеем

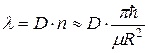. (7.19)

Если коэффициент прозрачности барьера удовлетворяет соотношению (7.15), то после подстановки и логарифмирования (7.19) мы получим закон Гейгера-Неттола (7.7).[58] Принимая энергию α-частиц T << В, можно приближенно определить, как зависят коэффициенты формулы (7.7) от А и Z радиоактивного ядра. Подставляя в (7.15) высоту кулоновского барьера (7.8) и учитывая, что при α-распаде Z₁ = Z_α = 2 и μ ≈ M_α, имеем

,

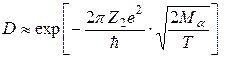где Z₂ – заряд дочернего ядра. Тогда логарифмируя (7.19), найдем, что

,

.

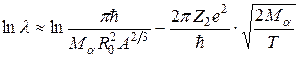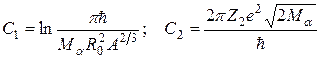Таким образом, С₁ очень слабо (логарифмически) зависит от массы ядра, а С₂ линейно зависит от его заряда.

Согласно (7.19), частота столкновений α-частицы с потенциальным барьером составляет для большинства α-радиоактивных около 5·10²⁰ с^–1.[59] Следовательно, величиной, определяющей постоянную α-распада оказывается коэффициент прозрачности барьера, сильно зависящий от энергии, так как последняя входит в показатель экспоненты. С этим и связана узость диапазона, в котором могут меняться энергии α-частиц радиоактивных ядер: частицы с энергиями выше 9 МэВ вылетают практически мгновенно, тогда как при энергиях ниже 4 МэВ они живут в ядре настолько долго, что α-распад очень трудно зарегистрировать.

Как уже отмечалось, спектры α-излучения часто имеют тонкую структуру, т.е. энергия испускаемых частиц принимает не одно, а целый ряд дискретных значений. Появление в спектре частиц с меньшей энергией (короткопробежных) соответствует образованию дочерних ядер в возбужденных состояниях. В силу закона (7.7) выход короткопробежных α-частиц всегда значительно меньше выхода частиц основной группы. Поэтому тонкая структура α-спектров связана, как правило, с переходами на вращательно возбужденные уровни несферических ядер с невысокой энергией возбуждения.

Если распад материнского ядра происходит не только из основного, но и из возбужденных состояний,[60] наблюдают длиннопробежные α-частицы. Примером могут служить длиннопробежные α-частицы, испускаемые ядрами изотопов полония ²¹²Po и ²¹⁴Po. Таким образом, тонкая структура α-спектров в ряде случаев несет информацию об уровнях не только дочерних, но и материнских ядер.

Учет того обстоятельства, что α-частица не существует в ядре, но образуется из составляющих ее нуклонов (двух протонов и двух нейтронов), а также более строгое описание движения α-частицы внутри ядра требуют и более детального рассмотрения физических процессов, происходящих в ядре. В связи с этим не приходится удивляться, что α-распады ядер подразделяются на облегченные и задержанные. Облегченным называется распад, для которого достаточно хорошо выполняется формула (7.19).[61] Если же реальный период полураспада превышает рассчитанный более чем на порядок,[62] такой распад называют задержанным.

Облегченный α-распад наблюдается, как правило, у четно-четных ядер, а задержанный – у всех остальных. Так, переходы нечетного ядра ²³⁵U в основное и первое возбужденное состояние ²³¹Th замедляются почти в тысячу раз. Если бы не данное обстоятельство, этот важный радионуклид (²³⁵U) оказался бы настолько короткоживущим, что не сохранился бы в природе к настоящему времени.

Качественно задержанный α-распад объясняется тем, что переход в основное состояние при распаде ядра, содержащего неспаренный нуклон (с наименьшей энергией связи) может иметь место только тогда, когда этот нуклон становится частью α-частицы, т.е. когда происходит разрыв другой пары нуклонов. Такой путь образования α-частицы значительно более затруднен, чем ее построение из уже существующих пар нуклонов в четно-четных ядрах. По этой причине и может происходить задержка перехода в основное состояние. Если, с другой стороны, α-частица все же образуется из пар нуклонов, уже существующих в таком ядре, дочернее ядро должно после распада оказаться в возбужденном состоянии. Последнее рассуждение объясняет довольно высокую вероятность перехода в возбужденные состояния для нечетных ядер (рис. 7.2).