Тема 8. Выборка: определение начального и конечного объемов.

Поскольку массовый опрос, анкетирование, как количественный метод, основан на применении теории вероятности, мы имеем возможность в математических терминах оценить достоверность и допустимые погрешности каждого добросовестно проведенного исследования.

Под доверительным интервалом понимают диапазон, в который попадет истинное значение изучаемого параметра генеральной совокупности при данном уровне достоверности. Чем он меньше, тем больше должна быть выборка.

Под, уровнем достоверности понимают вероятность того, что истинное значение изучаемого параметра генеральной совокупности попадет в доверительный интервал. Чем выше задаваемый уровень достоверности, тем больше должна быть выборка.

Важная задача маркетингового исследования – вычисление таких статистик, как выборочное среднее и выборочная доля, и применение их для оценки соответствующих истинных значений генеральной совокупности. Процесс распространения результатов оценки выборки на оценку генеральной совокупности называется статистическим заключением (statistical inference).

На практике создается одна выборка заданного объема и по ней вычисляются выборочные статистики (а именно, среднее и доля). Теоретически, для того чтобы оценить параметр изучаемой совокупности исходя из статистики выборки, нужно изучить каждую возможную выборку. Если бы все возможные выборки создавались в действительности, распределение статистики являлось бы выборочным распределением. Несмотря на то, что на практике создается только одна выборка, понятие выборочного распределения очень важно. Это дает возможность использовать теорию вероятности для того, чтобы делать выводы относительно значений совокупности.

Статистика (statistic) – описание характеристики выборки. Статистика выборки используется для оценки параметров генеральной совокупности.

Выборочное распределение (sampling distribution) – это распределение значений выборочных статистик, рассчитанных для каждой возможной выборки, которая формируется из изучаемой совокупности при определенном плане выборочного наблюдения.

Важные характеристики выборочного распределения среднего и соответствующие характеристики доли для больших выборок (30 и больше) следующие.

1. Выборочное распределение среднего для больших выборок (n = 30 и больше) можно свести к нормальному распределению.

2. Среднее значение по совокупности μ = сумма элементов совокупности/количество элементов

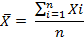
3. Стандартная ошибка (standard error) среднего или доли относится к выборочному распределению среднего или доли, а не к выборке или всей совокупности. В случае, если генеральная дисперсия 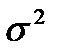(сумма квадратов отклонений каждого элемента выборки от генерального среднего / количество элементов совокупности) известна, используются следующие формулы для определения стандартной (среднеквадратической) ошибки:

Среднего: Доли:

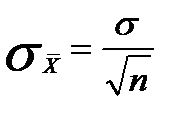
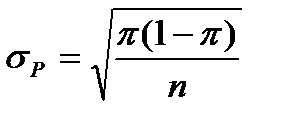
4. Часто среднеквадратичное отклонение изучаемой совокупности неизвестно. Тогда стандартная ошибка среднего может только оцениваться.

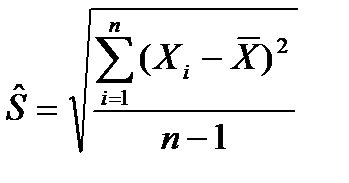, тогда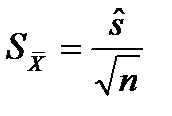

5. Если объем выборки составляет 10% или больше от объема исследуемой совокупности, применение формул стандартной ошибки приведет к переоценке среднеквадратичного отклонения среднего или доли совокупности, Значит, его следует откорректировать, применив коэффициент окончательной коррекции совокупности. Тогда формула стандартной ошибки будет выглядеть следующим образом:

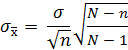
N – объем генеральной совокупности, n – объем выборки