Прыжковая функция и ее график

При заданном расходе и форме русла левая часть уравнения (18.1) есть функция глубины до прыжка h₁, а правая после прыжка – h₂.

Обозначив

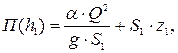(18.2)

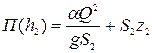, (18.3)

основное уравнение гидравлического прыжка (18.1) можно кратко переписать так

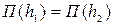. (18.4)

Величины П(h₁) и П(h₂) называются прыжковыми функциями сопряженных глубин и уравнение (18.4) читается так: прыжковые функции, вычисленные по сопряженным глубинам, равны между собой.

Прыжковая функция может быть представлена с помощью графика, вид которого приведен на рис. 18.3. Построение этого графика проводится следующим образом. При расчетном расходе Q и известной форме поперечного сечения русла задаются рядом значений h и по уравнению 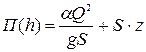вычисляют соответствующие значения функции П(h). Далее, откладывая по оси ординат значения глубин h, а по оси абсцисс – общие значения функции П(h), строят кривую прыжковой функции. Из рассмотрения графика прыжковой функции видно, что кривая П(h) имеет две ветви, уходящие в бесконечность (при h → 0 П(h) → ∞ и при h → ∞ П(h) → ∞), и что при некоторой глубине прыжковая функция имеет минимум (он достигается при глубине, равной критической). Из графика прыжковой функции, рис. 18.3, видно, что в пределах кривой П(h) одному значению функции П(h) соответствуют два значения h: одна глубина будет глубиной перед прыжком, а другая глубина – за прыжком. Из графика на рис. 18.3 следует также, что в данном открытом русле при заданном расходе Q может быть большое число сопряженных глубин, но каждой заданной глубине h₁ перед прыжком соответствует только одна

Рис. 18.3 сопряженная с ней глубина h₂.