Механическая система. Силы внешние и внутренние.

Механической системой называется такая совокупность материальных точек или тел, в которой положение или движение каждой точки или тела зависит от положения и движения всех остальных. Так, например, при изучении движения Земли и Луны относительно Солнца совокупность Земли и Луны является механической системой, состоящей из двух материальных точек, при разрыве снаряда на осколки мы рассматриваем осколки как механическую систему. Механической системой является любой механизм или машина.

Если расстояния между точками механической системы не изменяются при движении или покое системы, то такая механическая система называется неизменяемой.

Понятие неизменяемой механической системы позволяет изучать в динамике произвольное движение твердых тел. При этом, как в статике и кинематике, под твердым телом будем понимать такое материальное тело, у которого расстояния между каждыми двумя точками не изменяется при движении или покое тела. Любое твердое тело можно мысленно разбить на достаточно большое число достаточно малых частей, совокупность которых можно приближенно рассматривать как механическую систему. Так как твердое тело образует непрерывную протяженность, то для установления его точных (а не приближенных) свойств необходимо совершить предельный переход, предельное дробление тела, когда размеры рассматриваемых частей тела одновременно стремятся к нулю.

Таким образом, знание законов движения механических систем позволяет изучать законы произвольных движений твердых тел.

Все силы, действующие на точки механической системы, разделяют на внешние и внутренние силы.

Внешними силами по отношению к данной механической системе называются силы, действующие на точки этой системы со стороны материальных точек или тел, не входящих в систему. Обозначения: 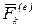—внешняя сила, приложенная к 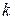-ой точке; 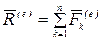—главный вектор внешних сил; 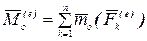—главный момент внешних сил относительно полюса.

Внутренними силами называются силы, с которыми материальные точки или тела, входящие в данную механическую систему, действуют на точки или тела этой же системы. Другими словами, внутренние силы–это силы взаимодействия между точками или телами данной механической системы. Обозначения: 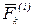—внутренняя сила, приложенная к 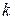-ой точке; 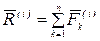—главный вектор внутренних сил; 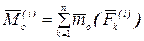—главный момент внутренних сил относительно полюса.

3.2 Свойства внутренних сил.

Первое свойство. Главный вектор всех внутренних сил механической системы равен нулю, то есть

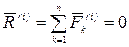. (3.1)

Второе свойство. Главный момент всех внутренних сил механической системы относительно любого полюса или оси равен нулю, то есть

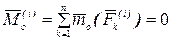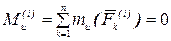, . (3.2)

Рис.17

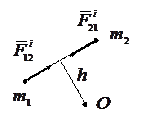Для доказательства этих свойств заметим, что, так как внутренние силы—это силы взаимодействия материальных точек, входящих в систему, то по третьему закону Ньютона любые две точки системы (рис. 17) действуют друг на друга с силам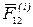и и 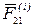, равными по модулю и противоположными по направлению.

Таким образом, для каждой внутренней силы имеется прямопротивоположная внутренняя сила и, следовательно, внутренние силы образуют некоторое множество попарно противоположных сил. Но геометрическая сумма двух прямо противоположных сил равна нулю, поэтому

.

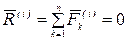Как было показано в статике, геометрическая сумма моментов двух прямо противоположных сил относительно одного и того же полюса равна нулю, поэтому

.

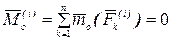Аналогичный результат получается и при вычислении главного момента относительно оси

.

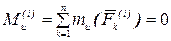3.3 Дифференциальные уравнения движения механической системы.

Рассмотрим механическую систему, состоящую из 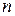материальных точек, массы которых 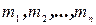. Для каждой точки 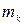применим основное уравнение динамики точки

, ,

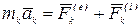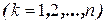или

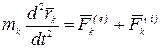, (3.3)

де 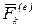—равнодействующая внешних сил, приложенная к 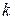-ой точке, а 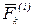—равнодействующая внутренних сил.

Систему 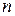дифференциальных уравнений (3.3) называют дифференциальными уравнениями движения механической системы в векторной форме.

Проектируя векторные уравнения (3.3) на прямоугольные декартовые оси координат получим дифференциальные уравнения движения механической системы в координатной форме:

,

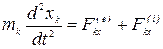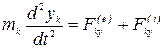, (3.4)

,

.

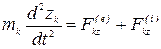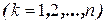Эти уравнение представляют собой систему 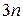обыкновенных дифференциальных уравнений второго порядка. Следовательно, для нахождения движения механической системы по заданным силам и начальным условиям для каждой точки этой системы, необходимо проинтегрировать систему 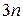дифференциальных уравнений. Интегрирование системы дифференциальных уравнений (3.4), вообще говоря, сопряжено со значительными, зачастую непреодолимыми математическими трудностями. Однако в теоретической механике разработаны методы, которые позволяют обойти основные трудности, возникающие при использовании дифференциальных уравнений движения механической системы в форме (3.3) или (3.4). К их числу относятся методы, которые дают общие теоремы динамики механической системы, устанавливающие законы изменения некоторых суммарных (интегральных) характеристик системы в целом, а не закономерности движения отдельных её элементов. Это так называемые меры движения—главный вектор количества движения; главный момент количества движения; кинетическая энергия. Зная характер изменения этих величин, удается составить частичное, а иногда и полное представление о движении механической системы.

IV. ОСНОВНЫЕ (ОБЩИЕ) ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ И СИСТЕМЫ

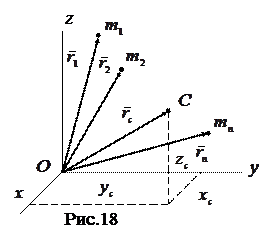4.1 Теорема о движении центра масс.

4.1.1.Центр масс механической системы.

Рассмотрим механическую систему, состоящую из 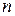материальных точек, массы которых .

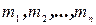Массой механической системы, состоящей из 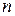материальных точек, будем называть сумму масс точек системы:

.

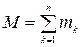Определение. Центром масс механической системы называется геометрическая точка 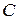, радиус вектор которой определяется по формуле:

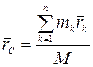, (4.1)

где 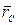—радиус-вектор центра масс; 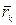—радиус-векторы точек системы; 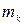—их массы (рис.18).

Проецируя (4.1) на декартовые оси координат получим формулы для координат центра масс

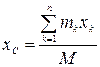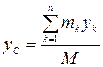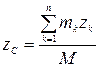; ; . (4.1')

Центр масс является не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой механической системы. В однородном поле силы тяжести центр масс совпадает с центром тяжести. Это, однако, не означает, что понятия центра масс и центра тяжести одинаковы. Понятие центра масс применимо к любым механическим системам, а понятие центра тяжести применимо только к механическим системам, находящимся под действием сил тяжести (то есть притяжения к Земле). Так, например, в небесной механике при рассмотрении задачи о движении двух тел, например Земли и Луны, можно рассматривать центр масс этой системы, но нельзя рассматривать центр тяжести.

Таким образом, понятие центра масс более широкое, чем понятие центра тяжести.

4.1.2. Теорема о движении центра масс механической системы.

Теорема. Центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему, то есть

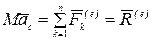. (4.2)

Здесь 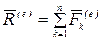—главный вектор внешних сил.

Доказательство. Рассмотрим механическую систему, материальные точки которой движутся под действием внешних и внутренних сил. 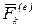—равнодействующая внешних сил, приложенная к 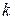-ой точке, а 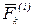—равнодействующая внутренних сил. Согласно (3.3) уравнение движения 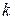-ой точки имеет вид

, .

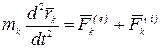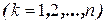Сложив левые и правые части этих уравнений, получим

.

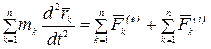Так как главный вектор внутренних сил равен нулю (п.3.2, первое свойство), то

.

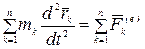Преобразуем левую часть этого равенства. Из формулы (4.1), определяющей радиус-вектор центра масс, следует:

.

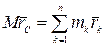Всюду в дальнейшем будем предполагать, что рассматриваются только механические системы постоянного состава, то есть 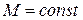и 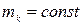. Возьмем от обеих частей этого равенства вторую производную по времени

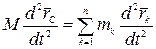
Так как 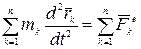, 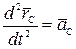—ускорение центра масс системы, то, окончательно,

.

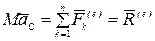Проектируя обе части этого векторного равенства на координатные оси, получим:

,

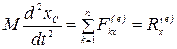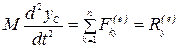, (4.3)

,

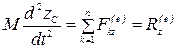где 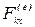, , 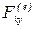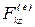—проекции силы ;

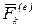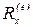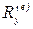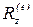, , —проекции главного вектора внешних сил 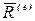на оси координат.

Уравнения (4.3)—дифференциальные уравнения движения центра масс механической системы в проекциях на декартовые оси координат.

Из уравнений (4.2) и (4.3) следует, что только одними внутренними силами нельзя изменить характер движения центра масс механической системы. Внутренние силы могут оказывать косвенное влияние на движение центра масс только через внешние силы. Например, в автомобиле внутренние силы, развиваемые двигателем, влияют на движение центра масс через силы трения колес с дорогой.

4.1.3. Законы сохранения движения центра масс

(следствия из теоремы).

Из теоремы о движении центра масс можно получить следующие следствия.

Следствие 1.Если главный вектор внешних сил, действующих на систему, равен нулю, то её центр масс находится в покое или движется прямолинейно и равномерно.

Действительно, если главный вектор внешних сил 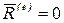, то из уравнения (4.2):

, .

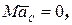
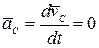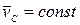Если, в частности, начальная скорость центра масс 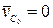, то центр масс находится в покое. Если же начальная скорость 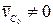, то центр масс движется прямолинейно и равномерно.

Следствие 2. Если проекция главного вектора внешних сил на какую-либо неподвижную ось равна нулю, то проекция скорости центра масс механической системы на эту ось не изменяется.

Это следствие вытекает из уравнений (4.3). Пусть, например, 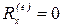, тогда

,

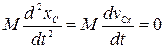отсюда 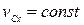. Если при этом в начальный момент 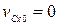, то:

, ,

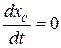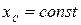то есть проекция центра масс механической системы на ось 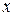в этом случае не будет перемещаться вдоль оси 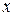. Если же 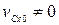, то проекция центра масс на ось 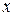движется равномерно.

4.2 Количество движения точки и системы.

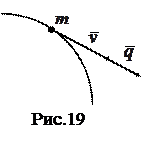Теорема об изменении количества движения.

4.2.1. Количество движения точки и системы.

Определение. Количеством движения материальной точки 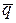называется вектор, равный произведению массы точки 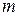на её скорость 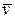, то есть

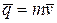. (4.5)

Вектор 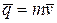коллинеарен вектору 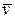и направлен по касательной к траектории материальной точки (рис.19).

Количество движения точки в физике часто называют импульсом материальной точки.

Размерность количества движения в СИ—кг·м/c или Н·с.

Определение. Количеством движения механической системы называется вектор 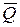, равный векторной сумме количеств движений (главный вектор количеств движений) отдельных точек, входящих в систему, то есть

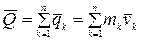(4.6)

Проекции количества движения на прямоугольные декартовые оси координат:

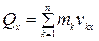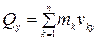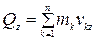; ; (4.7)

Вектор количества движения системы 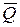в отличие от вектора количества движения точки 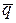не имеет точки приложения. Вектор количества движения точки приложен в самой движущейся точке, а вектор 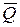является свободным вектором.

Лемма количеств движения. Количество движения механической системы равно массе всей системы, умноженной на скорость её центра масс, то есть

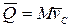(4.8)

Доказательство. Из формулы (4.1), определяющей радиус-вектор центра масс, следует:

.

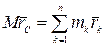Возьмем от обеих частей производную по времени

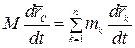, или .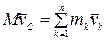

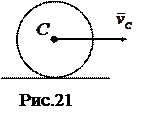
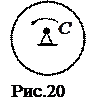Отсюда получим 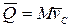, что и требовалось доказать.

Из формулы (4.8) видно, что если тело движется так, что его центр масс остается неподвижным, то количество движения тела равно нулю. Например, количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс (рис.20),

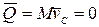, т.к.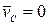

Если движение тела будет плоскопараллельным, то количество движения 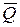не будет характеризовать вращательную часть движения вокруг центра масс. Например, для колеса, которое катится (рис.21), 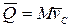независимо от того, каким образом происходит вращение колеса вокруг центра масс 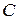. Количество движения 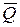характеризует только поступательную часть движения вместе с центром масс.

4.2.2. Теорема об изменении количества движения механической системы

в дифференциальной форме.

Теорема. Производная по времени от количества движения механической системы равна геометрической сумме (главному вектору) внешних сил, действующих на эту систему, т.е.

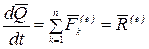. (4.9)

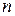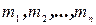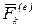
Доказательство. Рассмотрим механическую систему, состоящую из материальных точек, массы которых ; 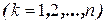—равнодействующая внешних сил, приложенная к 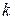-ой точке. В соответствии с леммой количества движения—формула (4.8):

.

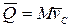Возьмем от обеих частей этого равенства производную по времени

.

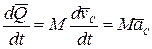Правая часть этого равенства из теоремы о движении центра масс—формула (4.2):

.

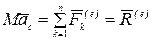Окончательно:

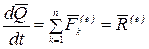
и теорема доказана.

В проекциях на прямоугольные декартовые оси координат:

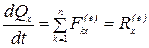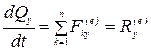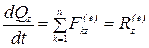; ; , (4.10)

то есть производная по времени от проекции количества движения механической системы на какую либо координатную ось равна сумме проекций (проекции главного вектора) всех внешних сил системы на ту же ось.

4.2.3. Законы сохранения количества движения

(следствия из теоремы)

Следствие 1. Если главный вектор всех внешних сил механической системы равен нулю, то количество движения системы постоянно по величине и направлению.

Действительно, если 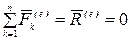, то из теоремы об изменении количества движения, т. е. из равенства (4.9) следует, что

.

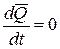Отсюда .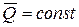

Следствие 2. Если проекция главного вектора всех внешних сил механической системы на некоторую неподвижную ось равна нулю, то проекция количества движения системы на эту ось остается постоянной.

Пусть проекция главного вектора всех внешних сил на ось 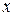равна нулю: 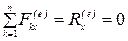. Тогда из первого равенства (4.10):

.

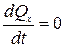Отсюда .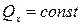

4.2.4. Теорема об изменении количества движения механической системы

в интегральной форме.

Элементарным импульсом силы называется векторная величина 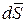, равная произведению вектора силы 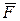на элементарный промежуток времени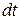

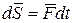. (4.11)

Направление элементарного импульса совпадает с направлением вектора силы.

Импульс силы за конечный промежуток времени 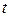равен определенному интегралу от элементарного импульса

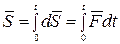. (4.12)

Если сила 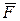постоянна по величине и направлению ( 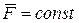), то ее импульс за время 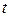равен:

.

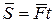Проекции импульса силы на оси координат:

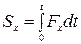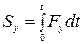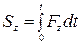, , . (4.13)

Докажем теорему об изменении количества движения механической системы в интегральной форме.

Теорема. Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил системы за этот же промежуток времени, т.е.

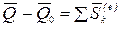(4.14)

Доказательство. Пусть в момент времени 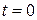количество движения механической системы равно 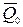, а в момент времени 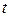— 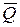; 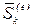—импульс внешней силы, действующей на 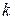-ю точку за время .

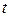Используем теорему об изменении количества движения в дифференциальной форме—равенство (4.9):

.

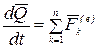Умножая обе части этого равенства на 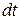и интегрируя в пределах от 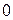до 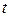, получим

, , .

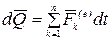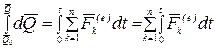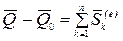Теорема об изменении количества движения в интегральной форме доказана.

В проекциях на оси координат согласно (4.14):

,

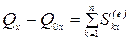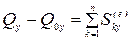, (4.15)

.

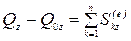4.3. Теорема об изменении кинетического момента.

4.3.1. Кинетический момент точки и системы.

В статике были введены и широко использовались понятия моментов силы относительно полюса и оси. Так как количество движения материальной точки 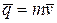является вектором, то можно определить его моменты относительно полюса и оси таким же образом, как определяются моменты силы.

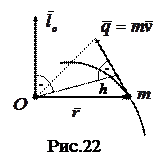Определение. Кинетическим моментом материальной точки 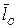относительно полюса 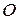называется момент её вектора количества движения относительно того же полюса 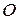, т. е.

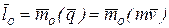. (4.16)

Кинетический момент материальной точки относительно полюса 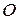представляет собой вектор 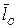(рис.22), направленный перпендикулярно плоскости, содержащей вектор 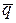и полюс 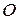в ту сторону, откуда вектор 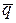относительно полюса 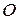виден направленным против вращения часовой стрелки. Модуль вектора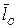

равен произведению модуля 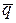на плечо 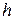—длина перпендикуляра, опущенного из полюса 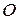на линию действия вектора :

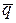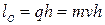
Кинетический момент относительно полюса может быть представлен в виде векторного произведения: кинетический момент материальной точки относительно полюса равен векторному произведению радиус вектора 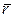, проведенного из полюса 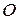в точку 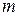на вектор количества движения :

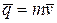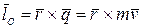(4.17)

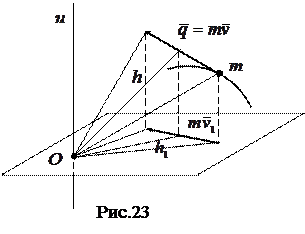Определение. Кинетическим моментом материальной точки 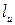относительно оси 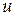называется момент её вектора количества движения относительно той же оси 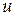, т. е.

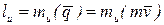. (4.18)

Кинетический момент 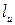материальной точки 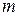относительно оси 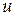(рис.23) равен взятому со знаком плюс или минус произведению проекции вектора 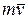на плоскость перпендикулярную к оси 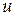, на плечо этой проекции :

,

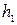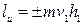где плечо 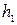—длина перпендикуляра опущенного из точки 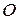пересечения оси 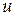с плоскостью на линию действия проекции 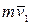, при этом 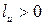, если, смотря навстречу оси 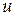, видно проекцию 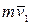относительно точки 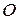направленной против вращения часовой стрелки, и 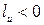в противном случае.

Размерность кинетического момента в СИ—кг·м²/с, или Н·м·с.

Определение. Кинетическим моментом или главным моментом количества движения 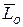механической системы относительно полюса называется вектор, равный геометрической сумме кинетических моментов всех материальных точек системы относительно этого полюса:

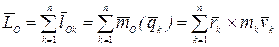. (4.19)

Определение. Кинетическим моментом или главным моментом количества движения механической системы 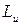относительно оси называется алгебраическая сумма кинетических моментов всех материальных точек системы относительно этой оси:

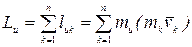. (4.20)

Кинетические моменты механической системы относительно полюса и оси, проходящей через этот полюс, связаны такой же зависимостью, как и главные моменты системы сил относительно полюса и оси:

—проекция кинетического момента механической системы относительно полюса 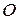на ось 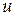, проходящую через этот полюс, равна кинетическому моменту системы относительно этой оси, т. е.

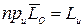. (4.21)

4.3.2. Теоремы об изменении кинетического момента механической системы.

Рассмотрим механическую систему, состоящую из 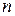материальных точек, массы которых 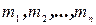. Докажем теорему об изменении кинетического момента механической системы относительно полюса.

Теорема. Производная по времени от кинетического момента механической системы относительно неподвижного полюса равна главному моменту внешних сил системы относительно того же полюса, т. е.

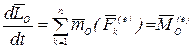. (4.22)

Доказательство. Выберем некоторый неподвижный полюс 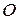. Кинетический момент механической системы относительно этого полюса по определению—равенство (4.19):

.

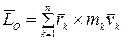Продифференцируем по времени это выражение:

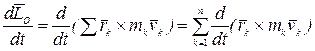. (4.23)

Рассмотрим правую часть этого выражения. Вычисляя производную произведения:

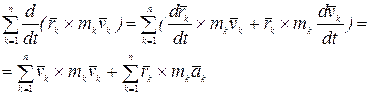, (4.24)

Здесь учтено, что 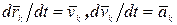. Векторы 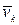и 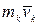имеют одинаковое направление, их векторное произведение равно нулю, следовательно, первая сумма в равенстве (4.24):

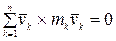. (4.25)

Рассмотрим вторую сумму:

.

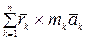Для каждой материальной точки механической системы применяем основное уравнение динамики точки:

, ,

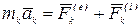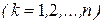где 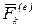—равнодействующая внешних сил механической системы, действующая на 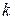–ю точку, 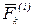—равнодействующая внутренних сил. Тогда:

=

,

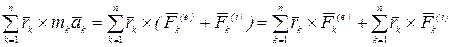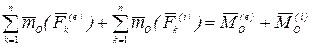где 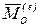—главный момент внешних сил относительно полюса 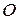, 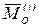—главный момент внутренних сил. По второму свойству внутренних сил механической системы (п. 3.2) 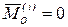и

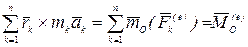. (4.26)

Учитывая равенства (4.26), (4.25) и (4.24) уравнение (4.23) принимает вид

.

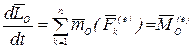Теорема доказана.

Докажем теорему об изменении кинетического момента механической системы относительно оси.

Теорема. Производная по времени от кинетического момента механической системы относительно неподвижной оси равна главному моменту внешних сил системы относительно той же оси, т. е.

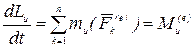. (4.27)

Доказательство. Выберем на неподвижной оси 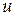произвольный полюс 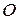. В соответствии с теоремой об изменении кинетического момента относительно полюса—формула (4.22):

.

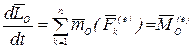Проектируем это векторное равенство на ось :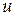

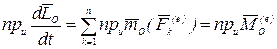. (4.28)

Из математики известно, что проекция производной вектор функции равна производной её проекции, т. е.

.

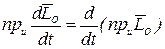Кроме того, кинетические моменты механической системы относительно полюса и оси связаны зависимостью (4.21):

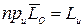
Тогда левая часть равенства (4.28) принимает вид:

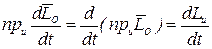. (4.29)

Для преобразования правой части равенства (4.28) используем известные из статики зависимость между моментом силы относительно полюса и оси:

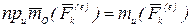(4.30)

и зависимость между главными моментами системы сил относительно полюса и оси:

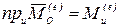. (4.31)

После подстановки (4.29), (4.30) и (4.31) в равенство (4.28) окончательно получаем

,

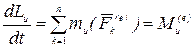и теорема доказана.

4.3.3. Законы сохранения кинетического момента

(следствия из теоремы)

Следствие 1. Если главный момент внешних сил системы относительно неподвижного полюса равен нулю, то кинетический момент этой системы относительно того же полюса будет постоянным как по величине, так и по направлению.

Действительно, на основании (4.22) имеем: 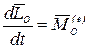. Если 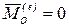, то .

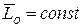Следствие 2. Если главный момент внешних сил системы относительно неподвижной оси равен нулю, то кинетический момент этой системы относительно той же оси будет постоянным.

Если 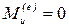, тогда по формуле (4.27): 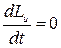и .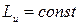

4.3.4. Кинетический момент твердого тела, вращающегося вокруг неподвижной оси, относительно оси вращения.

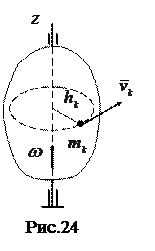Рассмотрим твердое тело, вращающееся вокруг неподвижной оси 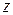с угловой скоростью 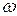(рис.24). Кинетический момент материальной точки

массы 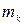относительно оси 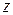(формула (4.18)):

.

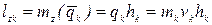Учитывая, что 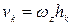, где 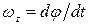—алгебраическая угловая скорость тела:

.

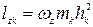Кинетический момент тела относительно оси будет, согласно (4.20), равен алгебраической сумме этих выражений для всех точек тела

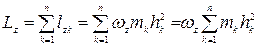(4.32)

Определение. Моментом инерции твердого тела

(механической системы) относительно оси называется сумма произведений масс всех точек тела (системы) на квадрат их расстояний от этой оси, т. е.

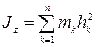(4.33)

Размерность момента инерции в системе СИ—кг·м². Часто при вычислениях применяют понятие радиуса инерции. Радиусом инерции тела относительно оси называется величина 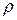, определяемая равенством

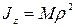, (4.34)

где 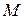—масса тела.

Возвращаясь к формуле (4.32), получаем

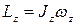, (4.35)

т. е. кинетический момент твердого тела, вращающегося вокруг неподвижной оси, относительно оси вращения равен произведению момента инерции тела относительно оси вращения на алгебраическую угловую скорость этого тела.

4.3.5. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.

Рассмотрим тело, вращающееся вокруг неподвижной оси, к которому приложены внешние силы 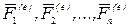(рис.25). Кроме этих сил, к числу

внешних сил относятся реакци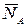и и 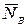подпятника 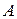и подшипника 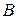; моменты этих реакций относительно оси вращения равны нулю.

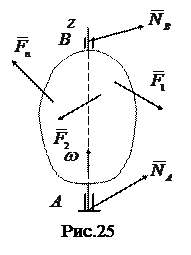
Применим теорему об изменении кинетического момента механической системы относительно оси (формула (4.27)):

.

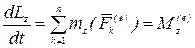Подставляя в это уравнение вместо кинетического момента 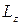выражение(4.35), и учитывая, что алгебраическое угловое ускорение 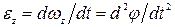, получим:

,

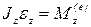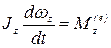, (4.36)

.

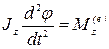Мы получили дифференциальное уравнение вращения твердого тела вокруг неподвижной оси в трех формах.

Дифференциальное уравнение вращения

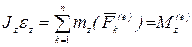
является аналогом основного уравнения динамики точки

.

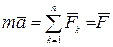По этой аналогии понятиям массы 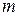, ускорения 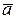, силы 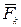при движении точки (и при прямолинейном поступательном движении тела) соответствуют при вращении твердого тела вокруг неподвижной оси: момент инерции 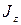—мера инертности тела при вращательном движении, угловое ускорение 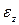и момент силы относительно оси .

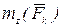4.3.6. Моменты инерции. Моменты инерции простых однородных тел.

Распределен