Критерии оценки систем

14.1. Оценка уровней качества систем с управлением

При оценивании качества систем с управлением целесообразно ввести несколько уровней качества, проранжированных в порядке возрастания сложности рассматриваемых свойств.

Эмпирические уровни качества получили названия: общая устойчивость, помехоустойчивость, управляемость, свойства, самоорганизация.

Рис. 14.1

Система, обладающая качеством данного порядка, имеет и все другие простые качества, но не имеет качеств более высокого порядка.

1) Первичные качеством любой системы является ее устойчивость. Для простых систем устойчивость объединяет такие свойства как прочность, стойкость к внешним воздействиям, сбалансированность, стабильность, гомеостазис. Для сложных систем характерны различные формы структурной устойчивости, такие как надежность, живучесть и т.д.

2) Более сложным качеством, чем устойчивость, является помехоустойчивость – способность системы без искажений воспринимать и передавать информационные потоки. Помехоустойчивость объединяет ряд свойств, присущих в основном системам управления. К таким свойствам относятся: надежность информационных систем и систем связи, их пропускная способность, возможность эффективного кодирования (декодирования) информации, электромагнитная совместимость и т.п.

3) Следующим по сложности качеством является управляемость – способность системы переходить за конечное (заданное) время в требуемое состояние под влиянием управляющих воздействий. Управляемость обеспечивается, прежде всего, наличием прямой и обратной связей, объединяет такие свойства системы, как гибкость управления, оперативность, точность, быстродействие, инерционность, связность, наблюдаемость объекта управления и др. Для сложных систем управляемость включает в себя способность принятия решений по формированию управляющих воздействий.

4) Следующим уровнем по шкале качеств являются свойства – это качество системы, определяющее ее возможности по достижению требуемого результата на основе имеющихся ресурсов за определенное время. Данное качество определяется такими свойствами, как результативность (производительность, мощность и т.п.), ресурсоемкость, эффективность – способность получить требуемый результат при идеальном способе использования ресурсов и в отсутствии воздействий внешней среды.

5) Наиболее сложным качеством системы является самоорганизация – способность системы для повышения эффективности изменять свою структуру, параметры, алгоритмы функционирования, поведения. Принципиально важными свойствами этого являются свобода выбора решений, адаптивность, самообучаемость, способность к распознаванию ситуаций и др.

Введение уровней качества позволяет ограничить исследование одним из перечисленных уровней. Для простых систем часто это исследование устойчивости.

Уровень качества выбирает исследователь в зависимости от сложности системы, целей анализа, наличие информации, условий работы системы.

14.2. Показатели и критерии оценки эффективности систем

Наиболее важные и принципиальные свойства системы можно классифицировать не только по уровню сложности, но и по тому, как они характеризуют процесс функционирования (поведение) системы.

В общем случае функциональные свойства системы оцениваются в двух аспектах:

– исход (результат) функционирования;

– «алгоритм», обеспечивающий получение результатов.

Качество исхода и «алгоритм», обеспечивающие получение результатов, оцениваются по показателям качества, которые вводятся с учетом конкретных особенностей системы и условий ее функционирования.

К основным укрупненным показателям качества функционирования систем относят: результативность, ресурсоемкость и оперативность.

Результативность 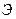характеризуется получаемым в результате целевым эффектом – результатом, ради которого функционирует система.

Ресурсоемкость 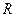отражает ресурсы всех видов (людские, материально – технические, энергетические, информационные, финансовые и.т.п.), используемые для получения целевого эффекта.

Оперативность 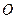есть измеритель расхода времени, потребного для достижения цели.

Оценка исхода функционирования системы (операции) учитывает, что операция проводится для достижения определенной цели – исхода операции. Под исходом операции понимается ситуация (состояние системы и внешней среды), возникающая на момент ее завершения. Для количественной оценки исхода операции вводится понятие показателя исхода ее (ПИО) в виде вектора:

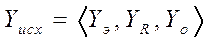, (14.1)

компоненты которого есть показатели его отдельных свойств, отражающие результативность, ресурсоемкость и оперативность операции.

Оценка «алгоритма» функционирования является ведущей при оценке эффективности системы, т.к. нужные результаты могут быть получены только при условии хорошего «алгоритма».

В совокупности результативность, ресурсоемкость и оперативность порождают комплексное свойство: эффективность процесса 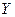– степень его приспособленности к достижению цели.

Выбор критерия эффективности – центральный, самый ответственный момент исследования системы.

Конкретный физический смысл показателей эффективности определяется характером и целями операций, а также качеством реализующей ее системы и внешними воздействиями.

Процесс выбора критерия эффективности, как и процесс определения цели, является в значительной мере субъективным, творческим, требующий в каждом отдельном случае индивидуального подхода.

Конкретный физический смысл показателей эффективности определяется характером и целями операции, а также качеством реализующей ее системы и внешними воздействиями.

В зависимости от типа систем и внешних воздействий операции могут быть детерминированными, вероятностными или неопределенными. В соответствии с этим выделяют три группы показателей и критериев эффективности:

А) показатели и критерии эффективности функционирования систем в известных условиях, если ПИО отражают один строго определенный исход детерминированной операции;

Б) показатели и критерии эффективности функционирования систем в условиях риска, ели ПИО являются дискретными или непрерывными случайными величинами с известными законами распределения;

В) показатели и критерии эффективности функционирования систем в условиях неопределенности, ее ли ПИО являются случайными величинами, законы, распределения которых неизвестны.

Критерий пригодности для оценки эффективности детерминированной операции имеет вид:

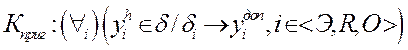(14.2)

Им определяется правило, по которому операция считается эффективной, если все частные показатели исхода операции принадлежат области адекватности.

Критерий оптимальности для оценки эффективности детерминированной операции имеет вид:

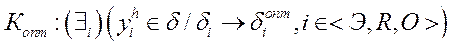(14.3)

Он определяет правило, по которому операция считается эффективной, если частные показатели ее исхода принадлежат области адекватности, а радиус этой области по указанным показателям оптимален.

Критерии пригодности для оценки эффективности вероятностной операции имеет вид:

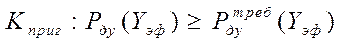(14.4)

и определяет правило, по которому операция считается эффективной, если вероятность достижения цели по показателям эффективности 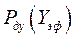не меньше требуемой вероятности достижения цели по этим показателям .

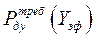Критерии оптимальности для оценки эффективности вероятностной операции имеет вид:

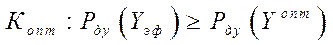(14.5)

и определяет правило, по которому операция считается эффективной, если вероятность достижения цели по показателям эффективности 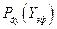больше или равна вероятности достижения цели с оптимальными значениями этих показателей .

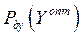Наибольшие трудности возникают при оценке эффективности систем в условиях неопределенности. Подходы для решения этой задачи составляют один из разделов теории принятия решений.

14.3. Методы качественного оценивания систем.

Методы оценивания систем разделяются на качественные и количественные.

Качественные методы используются на начальных этапах моделирования, если реальная система не может быть выражена в количественных характеристиках, отсутствует описание закономерностей систем в виде аналитических зависимостей.

Количественные методы используются на последующих этапах моделирования для количественного анализа вариантов системы.

Между этими крайними методами имеются и такие, с помощью которых стремятся охватить все этапы моделирования от постановки задачи до оценки вариантов. К ним относят:

– кибернетический подход к разработке адаптивных систем управления, проектирования и принятия решений;

– информационно–гносеологический подход к моделированию систем (основанный на общности процессов отражения, познания в системах различной физической природы);

– структурный и объективно–ориентированный подходы системного анализа;

– метод ситуационного моделирования;

– метод имитационного динамического моделирования.

Такие методы позволяют разрабатывать как концептуальные, так и строго формализованные модели, обеспечивающие требуемое качество оценки систем.

Простейшей формой задачи оценивания является обычная задача измерения, когда оценивание есть сравнение с эталоном, а решение задачи находится подсчетом числа эталонных единиц в измеряемом объекте.

Пример: 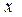– отрезок, 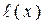– его длина.

Более сложные задачи оценивания разделяются на задачи парного сравнения, ранжирования, классификации, численной оценки.

Задача парного сравнения заключается в выявлении лучшего из 2х имеющихся объектов.

Задача ранжирования – в упорядочении объектов, образующих систему по убыванию (возрастанию) значения некоторого признака.

Задача классификации – в отношении заданного элемента к одному из множеств.

Задача численной оценки – в сопоставлении системе одного или нескольких чисел.

Перечисленные задачи могут быть решены непосредственно лицом, принимающим решение, или с помощью экспертов – специалистов в исследуемой области. В этом случае решение задачи оценивания называется экспертизой.

Качественные методы измерения и оценивания характеристик систем, используемые в системном анализе, достаточно многочисленны и разнообразны.

К основным относят:

1. методы «мозговой атаки» или коллективной генерации идей;

2. метод «сценариев»;

3. метод экспертных оценок;

4. метод «Дельфи»;

5. метод «дерева целей»;

6. морфологические методы.

1); 3) и 4) мы рассматривали в п.п.9 и 10.3.

Метод сценариев представляет собой процедуру подготовки и согласования представлений о проблеме или анализируемом объекте, изложенном в письменном виде.

Остановимся более подробно на характеристике последних 2х методов.

Термин «дерево целей» подразумевает использование иерархической структуры, полученной путем разделения общей цели на подцели, а их в свою очередь, на более детальные составляющие (новые подцели, функции и т.д.).

Разновидностью методов «дерева целей» и «Дельфи» является метод PATTERN (Planning Assistause Threng Technical Evalution of Relevance Number – помощь планированию посредством относительных показателей технической оценки), который по своей сути является комбинацией «дерева целей» и экспертных оценок.

Основная идея морфологических методов – систематически находить все мыслимые варианты решения проблемы или реализация системы путем комбинирования выделенных элементов или их признаков.

Наиболее широкое применение получил подход называемый «методом морфологического ящика» (ММЯ).

Построение и исследование по ММЯ состоит из следующих этапов:

1) Точная формулировка поставленной проблемы.

2) Выделение показателей 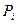от которых зависит решение проблемы.

3) Сопоставление показателю 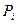его значений 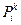и сведение этих значений в таблицу («морфологический ящик»).

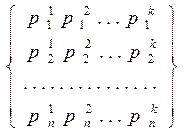
Оценка всех имеющихся в морфологической таблице (ящике) вариантов.

4) Выбор из морфологической таблицы наиболее желаемого варианта решения проблемы.

Для организационных систем такой ящик, как правило, многомерный, поэтому для использования этого метода разрабатывают языки моделирования или проектирования (системно – структурные языки).

14.4. Методы количественного оценивания систем. Общие положения

Первоначально задача количественного оценивания систем формировалась в терминах критерия превосходства в форме:

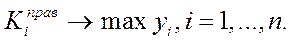
Однако поскольку большинство частных показателей качества связаны между собой так, что повышение качества системы по одному показателю ведет к понижению качества по другому, такая постановка была признана некорректной для большинства приложений.

Пример: 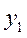– пропускная способность, 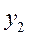– достоверность.

Для решения проблемы корректности критериев превосходства были разработаны методы количественной оценки систем:

– методы теории полезности;

– методы векторной оптимизации;

– методы ситуационного управления, инженерии знаний.

Методы теории полезности основаны на аксиоматическом использовании отношения предпочтения множества векторных оценок систем.

Методы векторной оптимизации базируются на использовании понятия векторного критерия качества систем (многокритериальные задачи).

Методы ситуационного управления основаны на построении таких моделей систем, в которых предпочтение формализуется в виде набора логических правил, по которым может быть осуществлен выбор альтернатив.

Рассмотрение указанных подходов в системном анализе основано на трех важных особенностях.

Во–первых, считается, что не существует оптимальной системы для всех целей и воздействий внешней среды. Система может быть эффективной только для конкретной цели и в конкретных условиях.

Во–вторых, считается, что не существует системы, наилучшей в независящем от ЛПР смысле, т.е. система может быть наилучшей лишь для данного ЛПР.

В–третьих, методы исследования операций (линейное, нелинейное, динамическое программирование и др.) не удовлетворяют требованиям, предъявляемым к задачам оценивания сложных организационных систем, поскольку вид целевой функции или неизвестен, или не задан аналитически, или для нее отсутствуют средства решения.

Общность подходов состоит в том, что оценивание систем по критериям производится с помощью шкал.

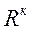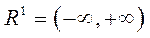Под К–мерной шкалой понимается соответствие эмпирической системы числовой системе , где – множество всех действительных чисел. Образы элементов эмпирической системы называются шкальными значениями или оценками по критерию.

Определение полезности как меры оценки того или иного исхода операции представляет сложную задачу, точные методы решения которой пока не найдены.

14.5. Оценка сложных систем в условиях определенности

Оценивание систем в условиях определенности производится с использованием методов векторной оптимизации с помощью шкал.

Пусть 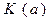– векторная оценка альтернативы 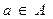; 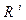– шкала (числовая система). Тогда общая задача векторной оптимизации может быть сформулирована следующим образом:

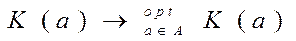(14.6)

Оценивание сложных систем в условиях определенности на основе методов векторной оптимизации проводится в три этапа.

На первом этапе с использованием системного анализа определяются частные показатели и критерии эффективности.

На втором этапе находится множество Парето и формулируется задача многокритериальной оптимизации в форме (14.6).

На третьем этапе задача (14.6) решается путем скаляризации критериев устранения многокритериальности.

Множество Парето – это подмножество А* множества альтернатив А, которое задается свойством его элементов:

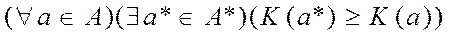(14.7)

Принцип Парето определяется выражением (14.2) и состоит в следующем: множество Парето А* (множество компромиссов) включает альтернативы, которые всегда более предпочтительны по сравнению с любой альтернативой из множества А\А*. При этом любые две альтернативы из множества Парето по предпочтению несравнимы.

Принцип Парето используется в тех случаях, когда задача многокритериальна и состоит в сравнении альтернатив между собой по всем сформированным критериям и выделении подмножества наилучших альтернатив. Решающее правило в этом случае строится на основе аксиомы Парето:

«Если в задаче принятия решений частные критерии независимы по предпочтению и значение каждого из них желательно увеличивать, то из двух альтернатив, характеризуемых набором частных критериев, предпочтительнее та, для которой выполняются соотношения 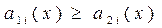по всем 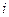, где первый индекс характеризует номер стратегии, второй индекс – номер частного критерия».

Таким образом, предпочтение одной альтернативы перед другой можно отдавать только если первая по всем критериям лучше второй.

В результате попарного сравнения альтернатив все худшие по всем критериям альтернативы отбрасываются, а все оставшиеся несравнимые между собой принимаются. Если все максимально достижимые значения частных критериев не относятся к одной и той же альтернативе, то принятые альтернативы образуют множество Парето и выбор на этом заканчивается.

Перейдем теперь к третьему этапу – устранению многокритериальности.

Наиболее употребительный способ – введение суперкритерия, т.е. скалярной функции векторного аргумента:

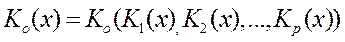
Вид функции 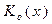определяется тем, как мы представляем себе вклад каждого критерия в суперкритерий (см. п. 6.2). Обычно для реализации данной процедуры используют аддитивные

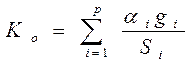
или мультипликативные функции

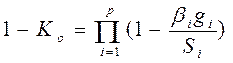
Коэффициенты 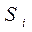обеспечивают безразмерность критериального значения. Коэффициенты 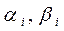отражают относительный вклад частных критериев в суперкритерий.

Тогда задача сводится к максимизации суперкритерия:

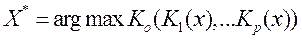
Очевидные достоинства объединения нескольких критериев в один суперкритерий сопровождаются рядом трудностей и недостатков, которые необходимо учитывать при использовании этого метода.

Рассмотрим один важный частный случай в качестве примера.

Пусть для каждого из частных критериев известен «идеал», к которому нужно стремиться. Обозначим его 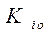. Тогда 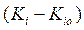– мера близости к идеалу. Для сопоставимости показателей приведем их к безразмерному значению следующим образом:

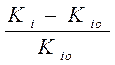
Чтобы исключить влияние знаков возведем это выражение в квадрат. Тогда обобщенный критериальный показатель можно записать

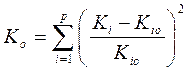
С учетом весовых коэффициентов, отражающих вклад каждого частного критерия, получим

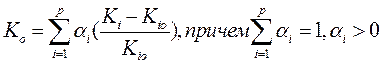
14.6. Оценка сложных систем на основе теории полезности

Функция полезности

В теории полезности исходят из того, что критерий эффективности предназначен для выявления порядка предпочтений на альтернативах (исходах операции), что позволяет обеспечить обоснованный выбор решений.

Выявить формально отношение предпочтения или безразличия непосредственным сравнением альтернатив трудно: показатели исходов операции многочисленны, имеют разный физический смысл и разные шкалы измерений (стоимость изготовления, численность обслуживающего персонала, пропускная способность, вероятность прохождения сигнала и т.д.). Деньги тоже не выступают универсальной мерой ценности. Вводится искусственная мера, которая определяется через полезность альтернатив (исходов). Чаще всего это действительное число, приписываемое исходу операции и характеризующее его предпочтительность по сравнению с другими альтернативами относительно цели.

Зная возможные альтернативы с их показателями полезности, можно построить функцию полезности, которая дает основу для сравнения и выбора решений.

Функция полезности представляет собой числовую ограниченную функцию 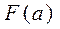, определенную на множестве альтернатив 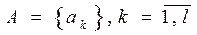, так, что 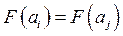, когда альтернативы 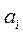и 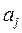неразличимы и 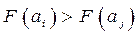, когда альтернатива 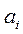предпочтительней альтернативы .

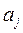В зависимости от типа показателей исходов операции функция полезности может быть либо непрерывной, либо дискретной.

Функцию полезности называют прямой, если чем больше значение показателя исхода операции, тем он полезнее, и обратной, если больше значение показателя исхода операции, тем он менее полезен.

Определение полезности как меры оценки того или иного исхода операции представляет сложную задачу, точные методы решения которой пока не найдены.

14.6.2. Оценка сложных систем в условиях риска на основе функции полезности

Операции, выполняемые в условиях риска, называются вероятностными. Это означает, что каждой альтернативе 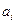ставится в соответствие не один, а множество исходов 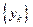с известными условными вероятностями появления .

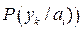Эффективность систем в вероятностных операциях находится через математические ожидания функции полезности на множестве исходов

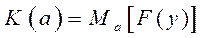
При исходах 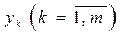с дискретными значениями показателей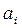

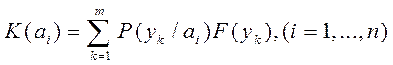
При исходах с непрерывными значениями

,

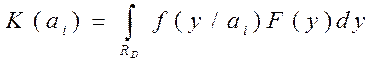где 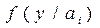– условная плотность вероятностей исходов.

Критерий оптимальности для вероятностных операций имеет вид:

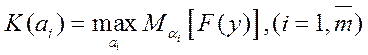
Кроме операции «в среднем» рассмотренной выше используются и другие критерии оценки систем:

– максимум вероятности случайного события;

– минимум среднего квадрата уклонения результата от требуемого;

– минимум дисперсии результата;

– минимум среднего (байесовского) риска;

– максимум вероятностно – гарантированного результата.

14.7. Оценка сложных систем в условиях неопределенности

В большом классе задач управления организационно–техническими системами отсутствуют объективные критерии оценивания достижения целевого и текущего состояний объекта управления, а также статистика, достаточная для построения соответствующих вероятностных распределений (законов распределения исходов операций) для конкретного принятого решения, что не позволяет их свести к детерминированным или вероятностным.

Условия оценки эффективности систем для неопределенных операций можно представить в виде таблицы.

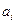
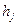
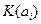
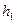
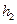
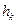
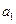
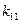
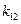
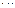
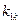
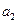
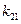
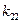
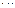
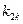
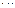
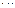
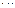
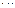
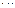
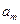
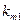
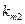
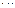
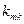
Здесь 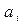– значение вектора управляемых параметров, определяющий свойства системы ;

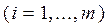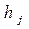– значение вектора неуправляемых параметров, определяющий состояние обстановки;

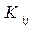– значение эффективности значения 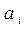для состояния обстановки ;

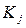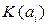– эффективность системы .

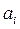В зависимости от характера неопределенности операции могут делиться на игровые и статистические неопределенные.

В игровых операциях неопределенность вносит своими сознательными действиями противник. Как в этом случае находится оптимальное решение, мы рассматривали в п.7.

Условия статистически неопределенных операций зависят от объективной действительности, называемой природой. В этом случае применяется теория статистических решений.

Единого критерия оценки эффективности для неопределенных операций не существует. Разработаны лишь общие требования к критериям оценки и выбора оптимальных систем. Основными требованиями являются:

1. оптимальное решение не должно меняться с перестановкой строк и столбцов матрицы эффективности;

2. оптимальное решение не должно меняться при добавлении тождественной строки или столбца к матрице эффективности;

3. оптимальное решение не должно меняться от добавления постоянного числа к значению каждого элемента матрицы эффективности;

4. оптимальное решение не должно становиться неоптимальным и, наоборот, в случае добавления новых систем, среди которых нет ни одной более эффективной системы;

5. если система 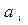и 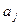оптимальны, то вероятностная смесь этих систем тоже должна быть оптимальна.

В зависимости от характера предпочтений ЛПР наиболее часто в неопределенных операциях используются критерии:

а) среднего выигрыша;

б) Лапласа;

в) осторожного наблюдателя (Вальда);

г) максимакса;

д) пессимизма–оптимизма (Гурвица);

е) минимального риска.

Пример: Необходимо оценить один из трех разрабатываемых программных продуктов 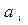для борьбы с одним из четырех типов программных воздействий .

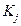Пусть дана матрица эффективности (рис. 14.2)

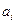
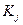
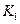
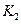
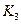
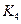
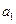
	0,1	0,5	0,1	0,2
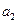
	0,2	0,3	0,2	0,4
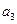
	0,1	0,4	0,4	0,3

Рис. 14.2

Здесь – 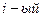программный продукт 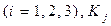– оценка эффективности применения 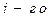программного продукта при 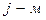программном воздействии .

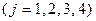а) критерий среднего выигрыша.

Данный критерий предполагает задание вероятностей состояний обстановки 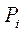. Эффективность систем оценивается как 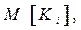т.е.

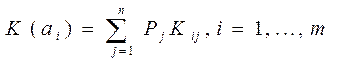
Оптимальной системы будет соответствовать эффективность

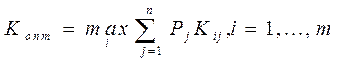
Пусть в нашем случае 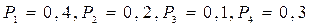. Тогда получим следующие оценки систем:

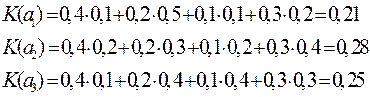
Оптимальное решение – система .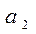

б) критерий Лапласа.

В основе критерия лежит предположение: поскольку о состоянии обстановки ничего не известно, то их можно считать равновероятностными. Исходя из этого:

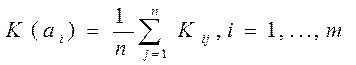
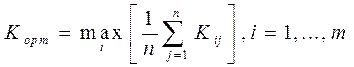
В нашем случае

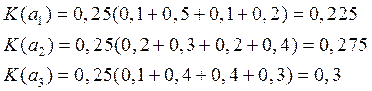
Оптимальное решение – система a₃. Критерий Лапласа представляет собой частный случай критерия среднего выигрыша.

в) критерий осторожного наблюдателя (Вальда) – это максиминный критерий, он гарантирует определенный выигрыш при наихудших условиях.

Оптимальной считается система из строки с максимальным значением эффективности:

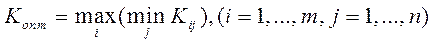
В нашем случае

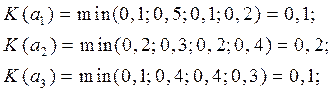
Оптимальное решение – система .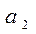

Максиминный критерий ориентирует на решение, не содержащее элементов риска; в этом его недостаток, другой – он не удовлетворяет условию 3.

г) критерий максимакса.

Критерий максимакса – самый оптимистический критерий. Те, кто предпочитают им пользоваться, всегда надеются на лучшее состояние обстановки, и естественно, в большей степени рискуют.

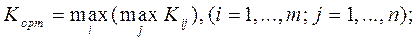
В нашем случае

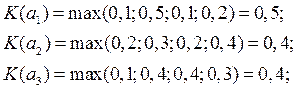
Оптимальное решение – система .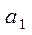

д) критерий пессимизма – оптимизма (Гурвица).

Это критерий обобщенного максимина. Для этого вводится коэффициент оптимизма 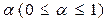, характеризующий отношение к риску лица, принимающего решение. Эффективность систем находится как взвешенная с помощью коэффициента 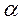сумма максимальной и минимальной оценок:

Условие оптимальности записывается в виде

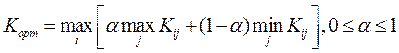
Пусть 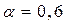и рассчитаем эффективность систем для рассматриваемого примера:

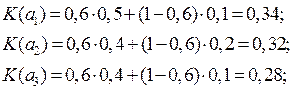
Оптимальное системой будет .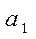

При 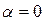критерий Гурвица сводится к критерию максимина, при 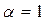– к критерию максимакса. На практике пользуются значениями коэффициента 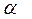в пределах 0,3–0,7. В критерии Гурвица не выполняются требования 4 и 5.

е) критерий минимального риска (Сэвиджа).

Этот критерий минимизирует потери при наихудших условиях.

Преобразуем матрицу эффективности в матрицу потерь (риска), в которой элементы определяются соотношением:

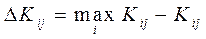
И используем критерий минимакса:

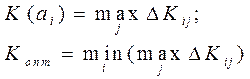
Обратимся опять к рассматриваемому примеру. В нем матрице эффективности будет соответствовать матрица потерь:

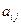
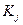
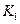
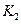
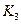
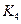
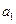
	0,1		0,3	0,2
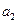
		0,2	0,2
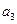
	0,1	0,1		0,1

Тогда

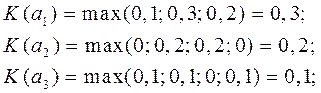
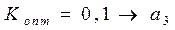
О критерии Сэвиджа можно сказать, что в нем по сравнению с критерием Вальда придается несколько большее значение выигрышу, чем проигрышу. Основной недостаток критерия – не выполняется требование 4.

Таким образом, эффективность систем в неопределенных операциях может оцениваться по целому ряду критериев. На выбор того или иного критерия оказывает влияние ряд факторов:

а) природа конкретной операции и ее цель (в одних операциях допустим риск, в других – важен гарантированный результат);

б) причины неопределенности (одно дело, когда неопределенность является случайным результатом действия объективных законов природы, и другое, когда она вызывается действиями разумного противника, стремящегося помешать в достижении цели);

в) характер лица, принимающего решения (одни люди склонны к риску, в надежде добиться большего успеха, другие предпочитают действовать всегда осторожно).