Плоская система произвольно расположенных сил

Силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого действия, переносить параллельно ей самой в любую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится (рис. 10).

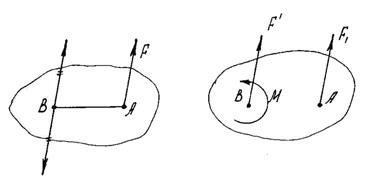
Рис. 10

Всякая плоская система сил, действующих на абсолютно твердое тело, при приведении к произвольно взятому центру О заменяет одной силой R, равной главному вектору системы и приложенной в центре приведения О, и одной парой с моментом М_О, равным главному моменту системы относительно центра О (рис. 11).

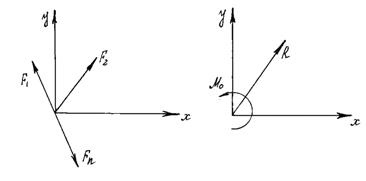
Рис. 11

Частные случаи приведения плоской системы сил к простейшему виду:

– если для данной системы сил R = 0 и М_О = 0, то она находится в равновесии;

– если для данной системы сил R = 0 и М_О ≠ 0, то она приводится к одной паре с моментом М_О = ∑m_О(F_i);

– если для данной системы сил R ≠ 0, М = 0, то она приводится к одной равнодействующей.

Основная форма условий равновесия.Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.

∑F_ix = 0 ∑F_iy = 0 ∑М_О(F_i) = 0

Вторая форма условий равновесия. Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма моментов всех этих сил относительно каких-нибудь двух центров А и В и сумма их проекций на ось Ох, не перпендикулярную к прямой АВ, были равны нулю.

∑F_ix = 0 ∑М_А(F_i) = 0 ∑М_В(F_i) = 0

Третья форма условий равновесия.Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма моментов всех этих сил относительно любых трех центров А, В, С, не лежащих на одной прямой, были равны нулю.

∑М_А(F_i) = 0 ∑М_В(F_i) = 0 ∑М_С(F_i) = 0