Зависимость коэффициента передачи тока эмиттера от частоты

В общем случае частотная зависимость коэффициента передачи тока эмиттера может быть представлена в виде, аналогичном стационарному режиму:

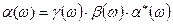. (7.76)

Определив частотные зависимости составляющих (7.76) и выделив действительную и мнимую часть, можно выразить АЧХ и ФЧХ транзистора.

Для оценки частотной зависимости эффективности эмиттера 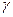воспользуемся эквивалентной схемой эмиттерного p-n перехода (рисунок 7.64). Инерционность эмиттера определяется временем перезаряда зарядной емкости эмиттера и установления неравновесной концентрации (перезаряд диффузионной емкости эмиттера) (5.76), (5.77). Диффу-зионная емкость эмиттера является частью общей диффузионной емкости p-n перехода.

Для 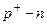эмиттера

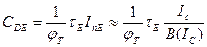, (7.77)

где 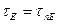для полубесконечного случая; 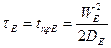, для эмиттера с ограниченной толщиной, .

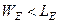Зависимость эффективности от частоты можно представить в виде:

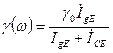, (7.78)

где 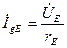– диффузионный ток;

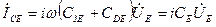– емкостной ток.

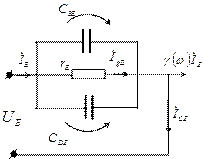
Рисунок 7.64 - Эквивалентная схема эмиттерного p-n перехода

Подставив значения диффузионного и емкостного токов в (7.78), получим:

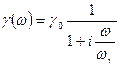, (7.79)

где 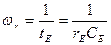– граничная частота эффективности, на которой модуль 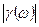уменьшается на 3 дБ или в 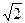раз.

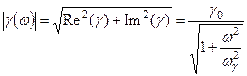. (7.80)

При 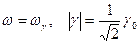. Фазовый сдвиг между входным током эмиттера 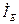и диффузионным током дырок, инжектируемых в базу 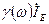составляет величину (рисунок 7.65, а):

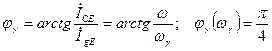. (7.81)

Амплитудно-частотная (7.80) и фазочастотная (7.81) характеристики представлены на рисунке 7.65. Физический смысл падения эффективности с ростом частоты заключается в увеличении доли емкостного тока в полном токе.

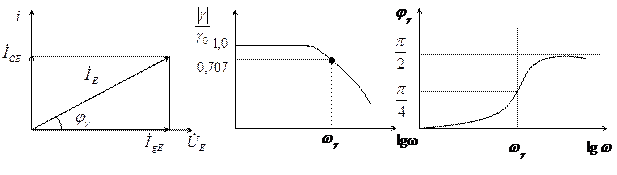а) б) в)

Рисунок 7.65 - Векторная диаграмма тока эмиттера (а), АЧХ (б) и ФЧХ (в) эффективности

Граничная частота коэффициента переноса.

Для бездрейфового транзистора зависимость коэффициента переноса от частоты определяется

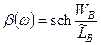, (7.82)

где 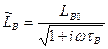– длина диффузионного смещения на переменном сигнале (5.83). Разлагая 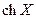в выражении (7.82) и ограничиваясь двумя членами разложения, получим:

; .

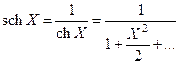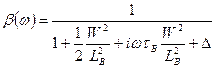Преобразуем к удобному виду:

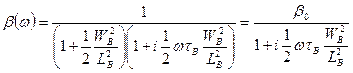. (7.83)

Выражение (7.83)представляет собой однополюсную функцию с емкостным характером реактивности:

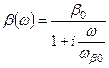, (7.84)

где 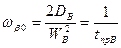– граничная частота коэффициента переноса.

Если учесть три члена в разложении (7.82), то значение граничной частоты примет вид:

.

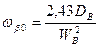Для дрейфового транзистора: .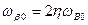

Амплитудночастотная характеристика 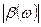хорошо аппроксимируется однополюсной функцией (7.84). Для фазочастотной характеристики эта аппроксимация дает плохое совпадение особенно для дрейфовых транзисторов. Поэтому для учета диффузионно-дрейфового механизма пролета базы и получения более точной зависимости фазы от частоты в формулу (7.84) вводят фазовый множитель:

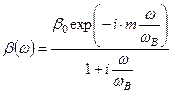, (7.85)

где 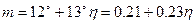- фазочастотная поправка.

Фазочастотная характеристика следует из (7.85) (рисунок 7.66):

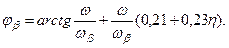(7.86)

Для бездрейфового транзистора на частоте ,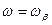

.

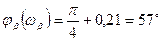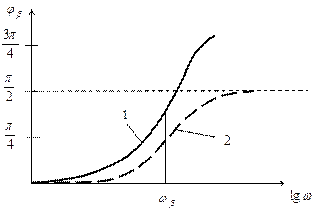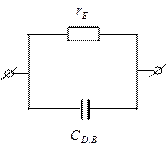Рисунок 7.66 - Фазочастотная характеристика Рисунок 7.67 - Эквивалентная схема для

коэффициента переноса (1) и однополюсная отражения инерционности пролета базы

аппроксимация (2)

Моделирование частотной зависимости модуля коэффициента переноса осуществляется с помощью параллельной RC- цепи (рисунок 7.67), постоянная времени которой равна времени пролета базы

.

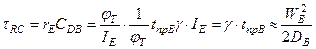Уменьшение модуля коэффициента переноса обусловлено увеличением рекомбинационных потерь при уменьшении периода (увеличении частоты) сигнала. В силу дискретности заряда распределение по скоростям носителей подчиняется закону Больцмана-Максвелла. Медленные носители не успевают пролететь базу и рекомбинируют, увеличивая ток базы и снижая коэффициент переноса.

Инерционность коллекторной цепи определяется временем перезаряда коллекторной емкости и временем пролёта ОПЗ коллектора. Постоянную времени коллекторной цепи оценим с помощью эквивалентной схемы (рисунок 7.68). Собственный коэффициент передачи коллектора

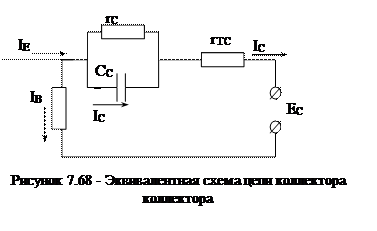
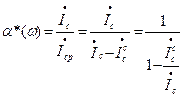, (7.87)

r’B

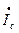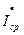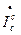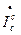где = + ; – емкостной ток коллектора. Так как r_C >> r’_B + r_TC, то цепь перезаряда С_СВ определяется r_TC и r’_B – омическими сопротивлениями тела базы и тела коллектора. Емкостный ток коллектора может быть выражен в виде:

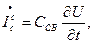
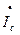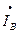где U_C(t)=E - r_TC – r’_B ; 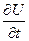= – r_TC – .

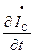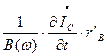Для гармонического сигнала,

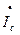=I₀e^iwt; .

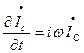Подставив это значение в выражение ёмкостного тока, получим:

.

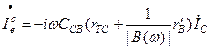Граничная частота для АЧХ в виде однополюсной функции определяется из условия |a(w)|=0,707, что соответствует |B(w)|=2,3. Подставив значение ёмкостного тока в (7.87), получим:

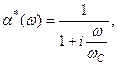(7.88)

где 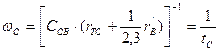– граничная частота цепи коллектора.

Для высокочастотных транзисторов необходимо учитывать влияние времени пролёта носителей заряда через ОПЗ коллекторного перехода на частотные свойства. По аналогии с пролётом базы коэффициент передачи тока при пролёте ОПЗ коллектора можно представить в виде:

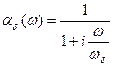, (7.89)

где 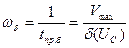; V_max – скорость дрейфа носителей в ОПЗ.

Для транзисторов, в которых проявляется заметно эффект Эрли, дополнительную инерционность вносит процесс перераспределения активного заряда базы при изменении толщины ОПЗ коллектора. Эта инерционность моделируется диффузионной ёмкостью коллектора, включённой параллельно зарядной ёмкости и дифференциальному сопротивлению коллектора (r_C). При этом постоянная времени перезаряда цепи r_C – C_DC равна времени пролёта базы.

, .

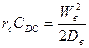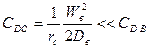В соответствии с рассмотренными инерционностями эквивалентная схема транзистора, отражающая частотную зависимость коэффициента передачи тока эмиттера представлена на рисунке 7.59.

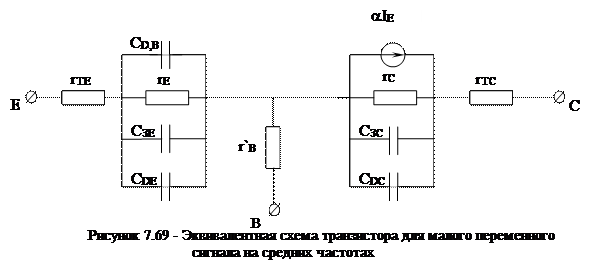В общем случае значения всех элементов, за исключением r_TE, зависят от стационарных режимов работы: тока, напряжения и температуры. Кроме того, из-за двумерности токораспределения наблюдается частотная зависимость 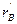и .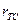

Для оценки приборной граничной частоты 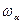необходимо определить модуль коэффициента передачи тока эмиттера.

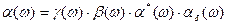, (7.90)

Решение (7.90) возможно численными методами. Задача упрощается, если предположить, что инерционности проявляются последовательно от эмиттера к коллектору.

Тогда суммарная инерционность 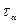будет представлять собой сумму всех постоянных времени:

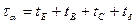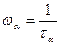; , (7.91)

.

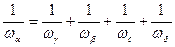В однополюсном представлении:

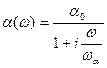, (7.92)

Выражение (7.92) удовлетворительно описывает АЧХ транзистора. Для отражения пролётных явлений и описания ФЧХ вносится фазочастотная поправка в виде (7.85).

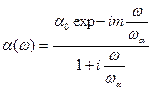, (7.93)

Фазочастотная характеристика из (7.93) имеет вид:

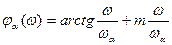, (7.94)