Теорема. Достаточные условия экстремума.
Правило 1. Если функция 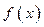 непрерывна в точке
непрерывна в точке 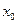 и дифференцируема в некоторой окрестности этой точки, за исключением, возможно, самой точки
и дифференцируема в некоторой окрестности этой точки, за исключением, возможно, самой точки 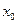 и при переходе через точку
и при переходе через точку 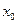 производная функции меняет знак с плюса на минус, то точка
производная функции меняет знак с плюса на минус, то точка 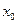 есть точка максимума функции
есть точка максимума функции 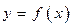 , а если с минуса на плюс, то точка минимума.
, а если с минуса на плюс, то точка минимума.
Если же при переходе через точку 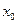 производная функции не меняет знак то в точке х0 функции
производная функции не меняет знак то в точке х0 функции 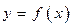 экстремума не имеет.
экстремума не имеет.
Доказательство. Для определенности рассмотрим случай, когда производная меняет знак с плюса на минус. Это значит, что слева от точки 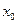 функция возрастает, т. е.
функция возрастает, т. е. 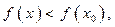 а справа — убывает т. е.
а справа — убывает т. е. 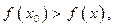 ч.т.д.
ч.т.д.
Правило 2. Если в окрестности точки 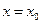 вторая производная непрерывна, причем
вторая производная непрерывна, причем 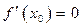 , а
, а 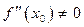 , то функция
, то функция 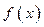 в точке x0 имеет экстремум, а именно максимум, если
в точке x0 имеет экстремум, а именно максимум, если 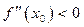 , и минимум, если
, и минимум, если 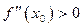 .
.
Доказательство. Рассмотрим случай 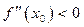 . Так как
. Так как 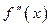 непрерывна, то существует некоторая окрестность точки
непрерывна, то существует некоторая окрестность точки 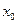 , в которой
, в которой 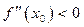 . Тогда в этой окрестности функция
. Тогда в этой окрестности функция 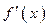 будет убывающей. Но при
будет убывающей. Но при 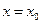 выполнено
выполнено 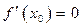 . Следовательно, при переходе (слева направо) через точку
. Следовательно, при переходе (слева направо) через точку 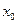 функция
функция 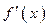 меняет знак с «плюса» на «минус». А это значит, что в точке
меняет знак с «плюса» на «минус». А это значит, что в точке 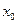 функция имеет максимум.
функция имеет максимум.
Правило 3. Пусть 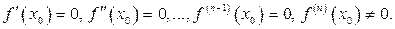 В этом случае функция
В этом случае функция 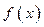 имеет в точке х0 экстремум, если n — четное число, а именно, максимум при
имеет в точке х0 экстремум, если n — четное число, а именно, максимум при 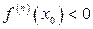 и минимум при
и минимум при 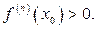 Если же n — нечетное число, то функция
Если же n — нечетное число, то функция 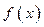 в точке х0 экстремума не имеет.
в точке х0 экстремума не имеет.
Для нахождения наибольшего (наименьшего) значения функции 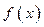 на отрезке
на отрезке 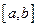 нужно из значений функции на границах отрезка и в критических точках, принадлежащих отрезку, выбрать наибольшее (наименьшее).
нужно из значений функции на границах отрезка и в критических точках, принадлежащих отрезку, выбрать наибольшее (наименьшее).
Пример 4.22.Найти интервалы монотонности, экстремумы функции 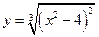 и построить ее график.
и построить ее график.
Решение.
1. 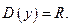
2. 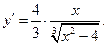
3. Находим критические точки первого рода: 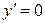 при
при 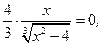
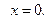
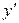 не существует при
не существует при 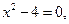
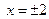 .
.
4. Критические точки разбили область определения на интервалы. Определяем знаки производной на каждом интервале.
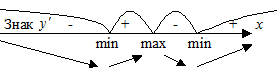
| x | 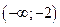
| -2 | 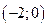
| 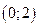
| 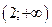
| ||
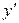
| - | 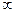
| + | - | 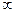
| + | |
| y | 
| 
| 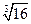
| 
| 
| ||
| min | max | min |
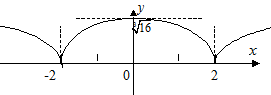
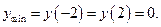
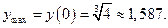
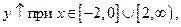
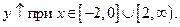
Строим график.
Рис. 4.14
Пример 4.23.Найти интервалы монотонности, экстремумы функции 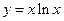 и построить ее график.
и построить ее график.
Решение.
1. 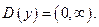
2. 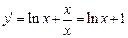 .
.
3. Находим критические точки первого рода. 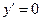 при
при 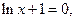
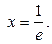
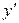 не существует: в области определения производная везде существует.
не существует: в области определения производная везде существует.
4. Критическая точка разбила область определения на интервалы. Определяем знаки производной на каждом интервале.
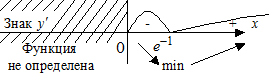
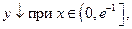
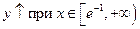 ,
, 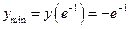 ,
, 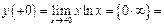
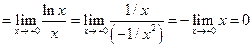 .
.
| x | 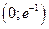
| 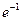
| 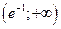
|
| - | + | |
| y | 
| min | 
|
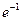
|
Строим график.
|


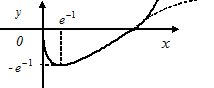
Рис. 4.15
Дата добавления: 2020-11-18; просмотров: 495;

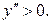 Если
Если