Метод избыточных величин Гиббса

Для определения характера изменения термодинамических свойств в поверхностном слое необходимо знать его протя­женность, т. е. объем или толщину. Свойства поверхностного слоя идентичны свойствам фазы на бесконечно большом рас­стоянии от поверхности раздела. Толщина поверхностного слоя 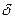неизвестна, неопределенна, т. к. поверхностный слой переходит в объемную фазу непрерывно. Значение d трудно определить экcпериментально вследствие малой величины и большой погрешности определений или рассчитать теорети­чески.

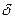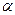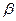У. Гиббс в 1876 г. предложил метод описания термодина­мики поверхностного слоя, основанный на исключении неоп­ределенности значения . Гиббс от реальной системы пере­шел к идеальной, заменив поверхностный слой разделяющей поверхностью, которая проводится внутри поверхностного слоя. Фазы и включают часть поверхно­стного слоя и считаются однородными вплоть до разделяю­щей поверхности. Гиббс предложил относить все изменения термодинамических параметров в слое по сравнению с объ­емными фазами к разделяющей поверхности, не имеющей объема, или толщины. Гиббс ввел два понятия: поверхность разрыва и разделяющую поверхность.

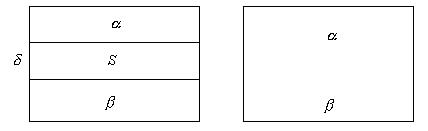
Рис. 2.6.

Поверхностный слой Гиббс называет поверхностью раз­рыва, понимая под этим неоднородный тонкий слой, разде­ляющий объемные фазы и обладающий конечной толщиной и объемом. Разделяющая поверхность – геометрическая по­верхность, воспроизводящая форму поверхности разрыва и располагающаяся параллельно ей. Разделяющая поверхность - фиктивная, воображаемая поверхность, на которой происхо­дит разрыв непрерывности в плоскостях 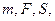состава. Ка­ждая точка вещества на поверхности находится в одинаковых условиях. Положение поверхности фиксируют, выбирая опре­деленную величину адсорбции на поверхности.

Разность между соответствующими экстенсивными вели­чинами в реальной и идеальной системе представляет собой избыточную величину, которую относят к разделяющей по­верхности. Посредством этих избытков выражаются все экс­тенсивные параметры в методе Гиббса, поэтому этот метод называется методом избыточных величин.

Фактически величины экстенсивных параметров для всей системы в целом несколько отличаются от их суммы для двух объемных фаз. Эту разность, положительную или отрицатель­ную, относят к разделяющей поверхности. При таком рассмот­рении поверхность характеризуется избыточными термодина­мическими параметрами, отражающими проявление поверх­ностной энергии. В соответствии с методом избыточных вели­чин энергия Гиббса двухфазной системы равна сумме энергий Гиббса отдельных фаз и поверхностной энергии Гиббса 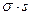, которая является избыточной.

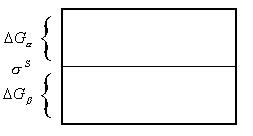
Рис. 2.7. Энергия Гиббса двухфазной системы с разделяющей поверхностью.

Избыток числа молей компонентов на поверхности

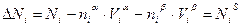
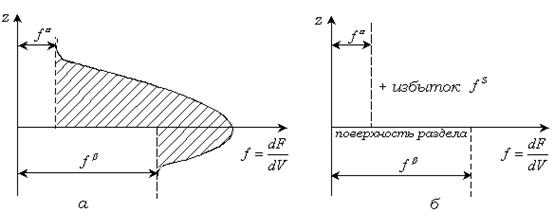
Рис. 2.8. Изменение плотности свободной энергии на межфазной границе в реальной системе ( 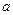) и в мо­дели Гиббса (б)

Таким образом, в методе Гиббса свойства реальной сис­темы отождествляются со свойствами идеальной системы, состоящей из двух фаз с разделяющей поверхностью, в кото­рой сосредоточены избытки термодинамических свойств. Из­менение плотности свободной энергии на границе фаз в ре­альной и идеальной системе показано на рис.

Метод Гиббса имеет существенные недостатки. Он приме­ним только к гетерогенным системам, состоящим из двух жид­ких фаз или жидкой и газообразной фазы. Проведение срав­нения реальной и идеальной систем и избыточных функций приводит к формальным затруднениям. Избыточные пара­метры зависят от положения разделяющей поверхности. На­конец, этот метод не позволяет рассмотреть свойства поверх­ностного слоя.

От этих недостатков свободен второй метод, называемый методом слоев конечной толщины. Согласно этому методу определяются не избыточные, а полные значения термодина­мических параметров в поверхностном слое. Избыток энергии Гиббса в системе определяется суммой избытков энергии Гиббса в каждой фазе и в поверхностном слое

Все величины, определяемые этим методом, имеют ясный физический смысл. Однако, трудно определять толщину по­верхностного слоя вследствие малой величины и неопреде­ленности этой характеристики.

2.6. Фундаментальное уравнение Гиббса для сво­бодной энергии гетерогенной системы с плоской границей раздела фаз

Пусть в гетерогенной системе, не способной к обмену ком­понентами со средой, т. е. закрытой системе, состоящей из га­зообразной фазы 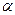и жидкой фазы 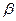объем увеличился на , а величина поверхности на .

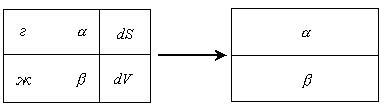
Рис. 2.9.

При этом совершается работа 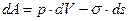. По­скольку увеличение объема происходит самопроизвольно, первый член этого выражения означает работу, совершенную системой самопроизвольно вследствие теплового движения. Увеличению поверхности система противится, поэтому второй член означает работу, совершенную над системой вследствие притока тепла извне.

Согласно первому закону термодинамики 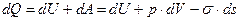. Согласно второму за­кону термодинамики при установлении равновесия 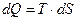. Объединим уравнения первого и второго закона термодинамики при установлении равновесия .

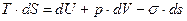1)

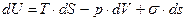
Перейдем от внутренней энергии к свободной энергии, т.е. заменим 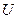на .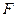

2)

Объединим уравнения 1) и 2)

Это - уравнение для закрытой гетерогенной системы с пло­ской границей раздела. Для открытой системы учитывается вещественный обмен, т.к. число молекул в системе может из­меняться, и уравнение принимает вид:

3)

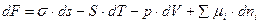
Это уравнение отличается от уравнения для гомогенной системы членом 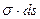, обозначающим работу образования поверхности. Из этого уравнения видно, что с увеличением поверхности увеличивается свободная поверхностная энер­гия. При увеличении числа компонентов также происходит увеличение свободной поверхностной энергии.

2.8. Уравнение Гиббса для плоского поверхност­ного слоя

Плоским поверхностным слоем называется такой слой, толщина которого много меньше радиуса кривизны, т. е. сис­тема отвечает условию: .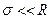

Для всей системы изменение свободной энергии определя­ется выражением 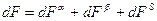. Согласно выраже­нию, полученному для системой с плоской границей раздела .

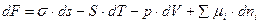В соответствии с методом избыточных величин Гиббса из­менение свободной энергии в поверхностном слое равно . Для каждой объемной фазы спра­ведливо выражение

4)

5)

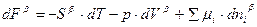
В этих выражениях у m_i нет индекса, т.к. при равновесии значения химического потенциала в обеих фазах выравнива­ются. Вычитая из выражения (3) выражения (4) и (5) и учиты­вая, что экстенсивные свойства 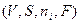суммируются и что при достижения равновесия 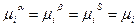, полу­чим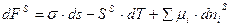

Свободная энергия поверхностного слоя складывается из трех членов: работы увеличения поверхности раздела фаз, энтропийного члена, учитывающего изменение связанной энергии системы и члена, учитывающего вещественный обмен между фазами и поверхностным слоем, т.е. состав поверхно­стного слоя.

Проанализируем это уравнение.

1. Возьмем частную производную 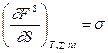. От­сюда получаем физический смысл 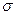, качественной характе­ристики поверхности. Поверхностное натяжение - это изме­нение свободной энергии поверхностного слоя, приходя­щееся на единицу увеличения поверхности. Чтобы увеличить поверхность, надо совершить работу. Отсюда вытекает второе определение: поверхностное натяжение - это обратимая изотермическая работа образования единицы поверхности, которая затрачивается на преодоление сил межмолекуляр­ного взаимодействия и переходит в свободную поверхност­ную энергию.

Объединенное уравнение первого и второго начал термо­динамики может быть записано и относительно других харак­теристических функций, а именно, энергии Гиббса 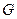, внут­ренней энергии , энтальпии 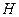. При соответствующих по­стоянных параметрах получим:

Таким образом, поверхностное натяжение есть частная производная от любой характеристической функции по площади межфазной поверхности при постоянных соответ­ствующих параметрах.

Наиболее часто поверхностное натяжение выражают через производную от энергии Гиббса, ибо условия 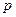и 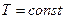легко осуществимы экспериментально. Для конденсированных систем можно пользоваться и производной от энергии Гельм­гольца, т.к. изменение объема от давления в конденсирован­ных системах мало.

Единицы измерения поверхностного натяжения:

в Си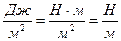

в СГС

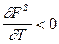2. . Экспериментально доказано, что на границе жидкости или твердого тела с газом с повышением температуры поверхностное натяжение уменьшается, т.к. уве­личивается расстояние между молекулами и уменьшается межмолекулярное взаимодействие. . Следовательно, и .

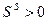Поверхностный слой на границе жидкости или твердого тела с газом обладает избыточной энтропией, которая всегда положительна. Причиной этого является переход молекул в менее плотную фазу, молекулы имеют больше степеней сво­боды.

3. .

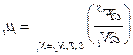Химический потенциал - это мольное приращение сво­бодной энергии при постоянном объеме при переходе i-го компонента в поверхностный слой. Химический потенциал характеризует скорость, с которой меняется свободная энер­гия при изменении концентрации данного вещества. Химиче­ский потенциал является движущей силой химических реак­ций. Аналогично поверхностному натяжению химический по­тенциал можно выразить как частную производную характери­стической функции по концентрации.