Степень с произвольным действительным показателем
Степени и корни
5.1 Корень 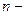 ой степени
ой степени
Для всякого числа a Î R определена степень с натуральным показателем an, n Î N.
Число b Î R называется корнем n-й степени, n Î N, n ³ 2, из числа а, если 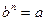 , обозначают
, обозначают 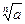 .
.
Нахождение корня n-й степени из данного числа а называют извлечением корня n-й степени из числа а. Число а, из которого извлекается корень n-й степени, называют подкоренным выражением, а число n – показателем корня.
Если 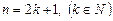 , то
, то 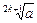 определен для всех a Î R и принимает любые действительные значения.
определен для всех a Î R и принимает любые действительные значения.
Если 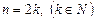 , то
, то 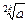 определен для всех a ³ 0 (aÎR). В курсе элементарной математики рассматривают арифметическое значение корня, т.е. число
определен для всех a ³ 0 (aÎR). В курсе элементарной математики рассматривают арифметическое значение корня, т.е. число 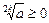 .
.
Свойства корней
Пусть a, b Î R. Тогда:
1) 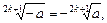
2) 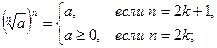
3) 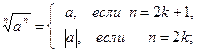
4) 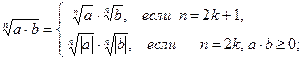
5) 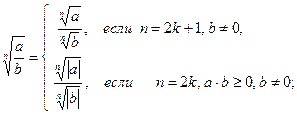
6) 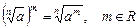 , (где a ³ 0 в случае
, (где a ³ 0 в случае 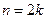 );
);
7) 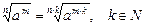 , (где
, (где 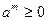 в случае
в случае 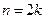 );
);
8) 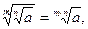 (где
(где 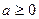 в случае
в случае 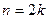 ).
).
Пример 1.Вычислить 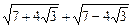 .
.
Решение. Способ 1. Выделим полные квадраты подкоренных выражений:
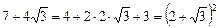 ;
;
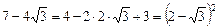 .
.
Тогда получим
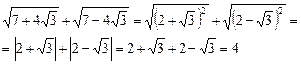 .
.
Способ 2. Обозначим вычисляемое выражение через a, т.е.
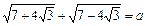 . Заметим, что
. Заметим, что 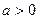 .
.
Возведем обе части полученного равенства в квадрат:
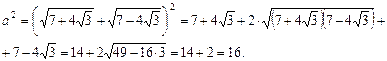
Тогда 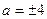 .
.
Поскольку исходное выражение положительно, в ответе получаем a = 4.
Пример 2. Упростить: 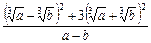 .
.
Решение. Способ 1. Используем формулы квадрата разности и суммы, а также свойства корней. Получаем
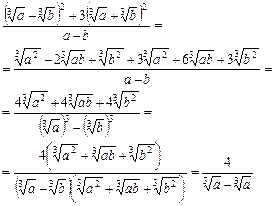 .
.
Способ 2. При упрощении иррациональных выражений часто бывает эффективным метод рационализации, основанный на замене переменных.
Введем такую замену переменных, чтобы корни извлеклись: 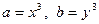 .
.
Заданное выражение приобретает вид
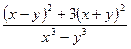 .
.
Упрощаем его, используя формулы сокращенного умножения:
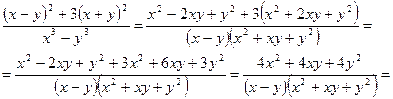
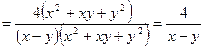 .
.
Возвращаясь к старым переменным, приходим к ответу 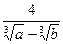 .
.
Пример 3. Избавиться от иррациональности в знаменателе:
1) 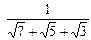 ; 2)
; 2) 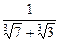 ; 3)
; 3) 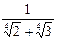 .
.
Решение.
1. Умножим числитель и знаменатель дважды на сопряженные выражения и воспользуемся формулой разности квадратов:
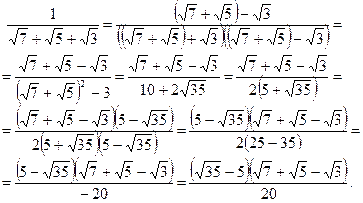
2. Домножим числитель и знаменатель на неполный квадрат разности и воспользуемся формулой суммы кубов:
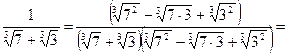
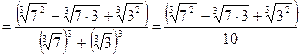 .
.
3. Умножим числитель и знаменатель дважды на сопряженные выражения:
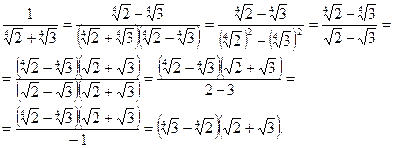
Задания
I уровень
1.1. Вычислите значения корней:
1) 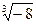 ; 2)
; 2) 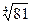 ; 3)
; 3) 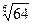 ;
;
4) 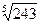 ; 5)
; 5) 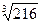 ; 6)
; 6) 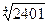 ;
;
7) 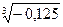 ; 8)
; 8) 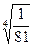 ; 9)
; 9) 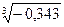 ;
;
10) 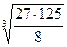 ; 11)
; 11) 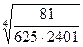 ; 12)
; 12) 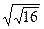 ;
;
13) 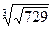 ; 14)
; 14) 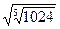 ; 15)
; 15) 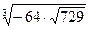 .
.
1.2. Сравните числа:
1) 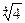 и
и 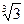 ; 2)
; 2) 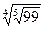 и
и 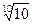 ;
;
3) 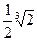 и
и 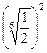 ; 4)
; 4) 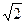 и
и 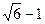 ;
;
5) 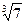 и
и 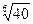 ; 6)
; 6) 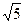 и
и 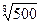 ;
;
7) 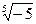 и
и 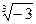 ; 8)
; 8) 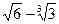 и 1;
и 1;
9) 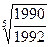 и
и 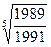 ; 10)
; 10) 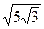 и
и 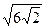 ;
;
11) 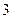 и
и 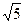 ; 12)
; 12) 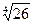 и
и 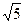 ;
;
13) 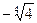 и
и 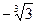 ; 14)
; 14) 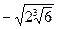 и
и 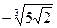 .
.
1.3. Упростите выражение:
1) 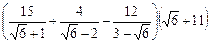 ;
;
2) 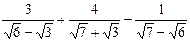 ;
;
3) 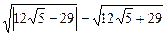 ;
;
4) 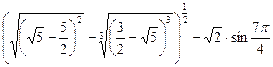 ;
;
5) 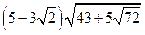 ; 6)
; 6) 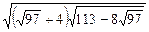 ;
;
7) 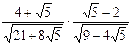 ; 8)
; 8) 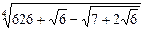 ;
;
9) 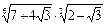 ; 10)
; 10) 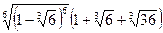 ;
;
11) 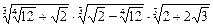 ;
;
12) 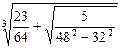 ; 13)
; 13) 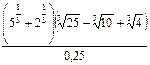 ;
;
14) 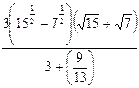 ; 15)
; 15) 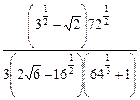 .
.
1.4. Избавьтесь от иррациональности в знаменателе:
1) 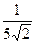 ; 2)
; 2) 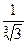 ; 3)
; 3) 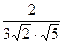 ;
;
4) 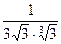 ; 5)
; 5) 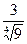 ; 6)
; 6) 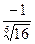 ;
;
7) 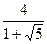 ; 8)
; 8) 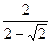 ; 9)
; 9) 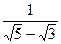 ;
;
10) 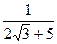 ; 11)
; 11) 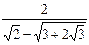 ;
;
II уровень
2.1. Упростите выражение:
1) 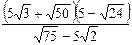 ;
;
2) 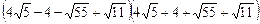 ;
;
3) 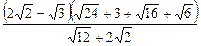 ;
;
4) 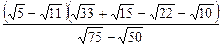 ;
;
5) 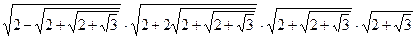
6) 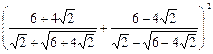 ;
;
7) 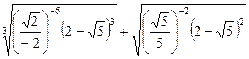 ;
;
8) 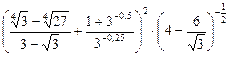 ;
;
9) 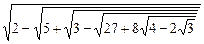 .
.
2.2. Избавьтесь от иррациональности в знаменателе:
1) 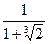 ; 2)
; 2) 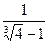 ;
;
3) 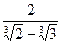 ; 4)
; 4) 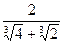 ;
;
5) 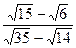 ; 6)
; 6) 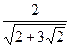 ;
;
7) 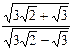 ; 8)
; 8) 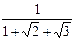 ;
;
9) 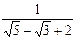 ; 10)
; 10) 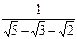 ;
;
11) 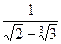 ; 12)
; 12) 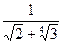 ;
;
13) 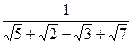 .
.
2.3. Упростите выражение:
1) 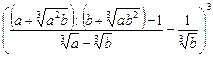 ;
;
2) 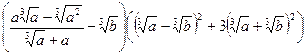 .
.
III уровень
3.1. Упростите выражение:
1) 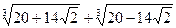 ; 2)
; 2) 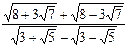 ;
;
3) 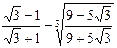 ; 4)
; 4) 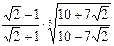 ;
;
5) 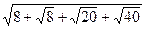 ; 6)
; 6) 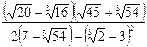 ;
;
7) 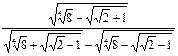 ;
;
8) 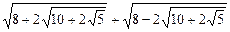 .
.
3.2. Избавьтесь от иррациональности в знаменателе:
1) 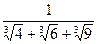 ; 2)
; 2) 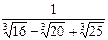 ;
;
3) 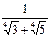 ; 4)
; 4) 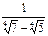 ;
;
5) 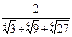 ; 6)
; 6) 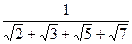 ;
;
7) 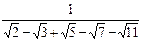 ; 8)
; 8) 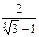 ;
;
9) 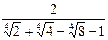 ; 10)
; 10) 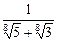 ;
;
11) 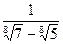 ; 12)
; 12) 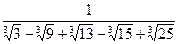 .
.
Степень с произвольным действительным показателем
Во множестве R определена степень ax с действительным показателем.
В выражении ax число а называют основанием степени, число x показателем степени. Нахождение значения степени называют возведением в степень.
Степень с действительным показателем
Пусть a Î R, тогда:
1) 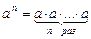 , n Î N;
, n Î N;
2) 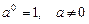 ;
;
3) 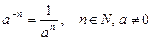 ;
;
4) 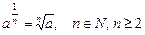 и a ³ 0, если
и a ³ 0, если 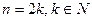 ;
;
5) 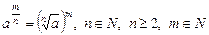 и если
и если 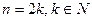 , то a ³ 0
, то a ³ 0
6) 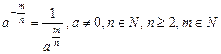 и если
и если 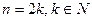 , то
, то 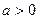 ;
;
7) 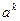 , где
, где 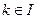 , определяется следующим образом.
, определяется следующим образом.
Пусть иррациональное число k записано в виде десятичной дроби, 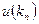 – последовательность его десятичных приближений с недостатком (или с избытком). Для любого действительного числа а > 0 степень
– последовательность его десятичных приближений с недостатком (или с избытком). Для любого действительного числа а > 0 степень 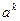 с иррациональным показателем определяется равенством
с иррациональным показателем определяется равенством
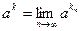 .
.
На множестве R не определены отрицательная и нулевая степень числа 0, а также 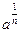 , если
, если 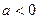
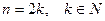 .
.
Свойства степеней
Допустим, что a, b, c Î R и это такие числа, что все степени имеют смысл. Тогда:
1) 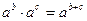 ;
;
2) 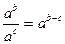 ;
;
3) 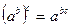 ,
,
4) 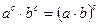 ;
;
5) 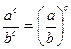 ;
;
6) если a > 1 и x < y, то 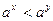 ,
,
если 0 < a < 1 и x < y, то 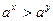 ;
;
7) если 0 < a < b и x >0, то 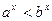 ,
,
если 0 < a < b и x < 0, то 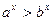 .
.
Пример 1. Вычислить 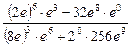 .
.
Решение. Используем свойства степеней
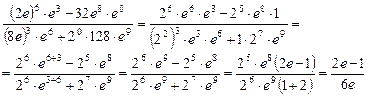
Пришли к ответу: 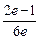 .
.
Задания
1.1. Представьте в виде степени с рациональным показателем:
1) 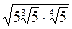 ; 2)
; 2) 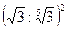 ;
;
3) 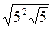 ; 4)
; 4) 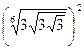 ;
;
5) 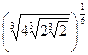 ; 6)
; 6) 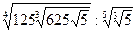 ;
;
7) 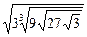 ; 8)
; 8) 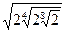 ;
;
9) 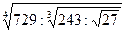 ; 10)
; 10) 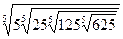 ;
;
11) 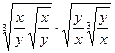 ; 12)
; 12) 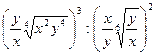 ;
;
13) 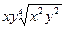 ; 14)
; 14) 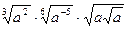 .
.
1.2. Выполните действия:
1) 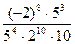 ; 2)
; 2) 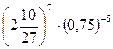 ;
;
3) 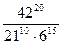 ; 4)
; 4) 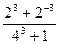 ;
;
5) 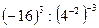 ; 6)
; 6) 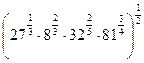 ;
;
7) 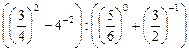 ;
;
8) 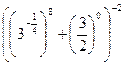 ; 9)
; 9) 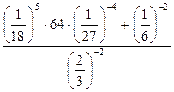 .
.
1.3. Найдите 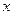 из уравнения:
из уравнения:
1) 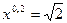 ; 2)
; 2) 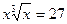 ;
;
3) 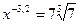 ; 4)
; 4) 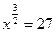 ;
;
5) 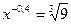 ; 6)
; 6) 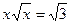 .
.
1.4. Упростите выражение:
1) 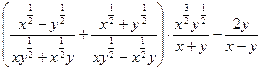 .
.
II уровень
2.1. Вычислите:
1) 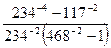 ;
;
2) 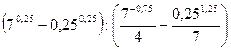 ;
;
3) 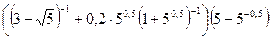 ;
;
4) 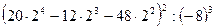 ;
;
5) 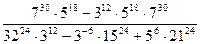 ;
;
6) 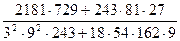 .
.
2.2. Упростите выражение:
1) 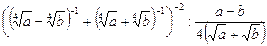 ;
;
2) 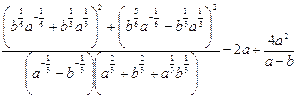 ;
;
3) 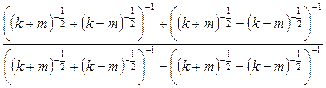 .
.
III уровень
3.1. Вычислите:
1) 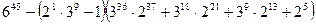 ;
;
2) 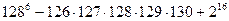 ;
;
3) 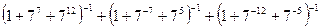 .
.
4) 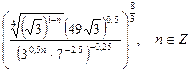 ;
;
5) 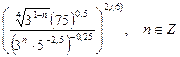 .
.
3.2. Найдите значение выражения:
1) 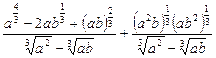 при
при 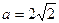 ;
;
2) 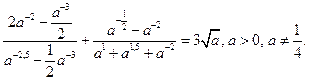
Степенная функция
Функция 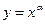 , где
, где 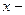 переменная величина,
переменная величина, 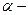 заданное число, называется степенной функцией.
заданное число, называется степенной функцией.
Если 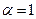 , то
, то 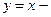 линейная функция, ее график прямая линия (см. 4.3.).
линейная функция, ее график прямая линия (см. 4.3.).
Если 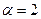 , то
, то 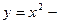 квадратичная функция, ее график – парабола (см. 4.3.).
квадратичная функция, ее график – парабола (см. 4.3.).
Если 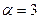 , то
, то 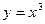 , ее график – кубическая парабола (см. 4.3.).
, ее график – кубическая парабола (см. 4.3.).
Степенная функция 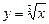 .
.
Это обратная функция для 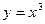 .
.
1Область определения: 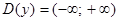 .
.
2Множество значений: 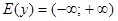 .
.
3Четность и нечетность: функция нечетная.
4Периодичность функции: не периодическая.
5Нули функции: x = 0 –единственный нуль.
6Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет.
7Промежутки возрастания и убывания: функция является возрастающей на всей области определения.
8График функции симметричен графику кубической параболы относительно прямой y = x и изображен на рис. 1.
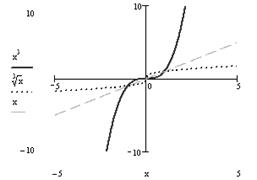
Рис. 1
Степенная функция 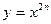 ,
, 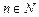 .
.
1. Область определения: 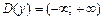 .
.
2. Множество значений: 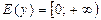
3. Четность и нечетность: функция четная.
4. Периодичность функции: не периодическая.
5. Нули функции: единственный нуль x=0.
6. Наибольшее и наименьшее значения функции: принимает наименьшее значение для x=0, оно равно 0.
7. Промежутки возрастания и убывания: функция является убывающей на промежутке 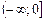 и возрастающей на промежутке
и возрастающей на промежутке 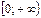 .
.
8. График функции (для каждого n Î N) «похож» на график квадратичной параболы 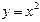 (графики функций
(графики функций 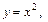
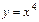 изображены на рис. 2.
изображены на рис. 2.
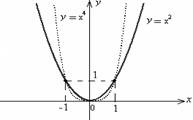
Рис. 2
Степенная функция 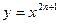 ,
, 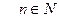 .
.
1. Область определения: 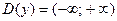 .
.
2. Множество значений: 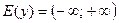
3. Четность и нечетность: функция нечетная.
4. Периодичность функции: не периодическая.
5. Нули функции: x=0 – единственный нуль.
6. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет при любом 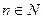 .
.
7. Промежутки возрастания и убывания: функция является возрастающей на всей области определения.
8. График функции (для каждого 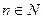 ) «похож» на график кубической параболы.
) «похож» на график кубической параболы.
(графики функций 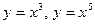 изображены на рис. 3).
изображены на рис. 3).
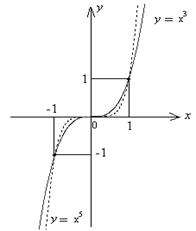
Рис. 3
Степенная функция, 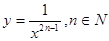 .
.
1Область определения: 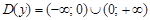 .
.
2Множество значений: 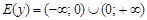 .
.
3Четность и нечетность: функция нечетная.
4Периодичность функции: не периодическая.
5Нули функции: нулей не имеет.
6Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет при любом 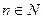 .
.
7Промежутки возрастания и убывания: функция является убывающей в области определения.
8Асимптоты: 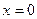 (ось Оу) – вертикальная асимптота;
(ось Оу) – вертикальная асимптота;
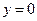 (ось Ох) – горизонтальная асимптота.
(ось Ох) – горизонтальная асимптота.
9График функции (для любого n) похож на график гиперболы (графики функций 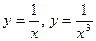 изображены на рис. 4).
изображены на рис. 4).
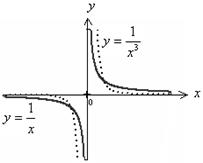
Рис. 4
Степенная функция, 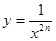 ,
, 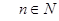 .
.
1Область определения: 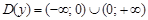 .
.
2Множество значений: 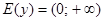 .
.
3Четность и нечетность: функция четная.
4Периодичность функции: не периодическая.
5Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет при любом 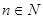 .
.
6Промежутки возрастания и убывания: функция является возрастающей на 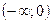 и убывающей на
и убывающей на 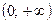 .
.
7Асимптоты: x = 0 (ось Оу) – вертикальная асимптота;
y = 0 (ось Ох) – горизонтальная асимптота.
8Графиками функций являются квадратичные гиперболы (рис. 5).
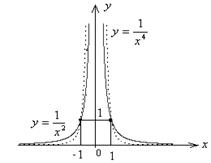
Рис. 5
Степенная функция, 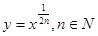
1Область определения: 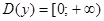 .
.
2Множество значений: 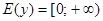 .
.
3Четность и нечетность: функция не обладает свойством четности и нечетности.
4Периодичность функции: не периодическая.
5Нули функции: x=0 – единственный нуль.
6Наибольшее и наименьшее значения функции: наименьшее значение, равное 0, принимает в точке x=0; наибольшего значения не имеет.
7Промежутки возрастания и убывания: функция является возрастающей на всей области определения.
8Каждая такая функция при определенном показателе является обратной для 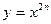 при условии
при условии 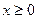 .
.
9График функции «похож» на график функции 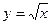 при любом n и изображен на рис. 6.
при любом n и изображен на рис. 6.
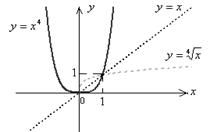
Рис. 6
Степенная функция, 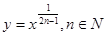 .
.
1Область определения: 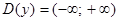 .
.
2Множество значений: 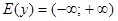 .
.
3Четность и нечетность: функция нечетная.
4Периодичность функции: не периодическая.
5Нули функции: x=0 – единственный нуль.
6Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет при любом 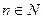 .
.
7Промежутки возрастания и убывания: функция является возрастающей на всей области определения.
8График функции изображен на рис. 7.
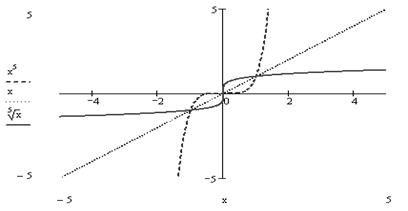
Рис. 7
Пример 1. Построить график функции:
1) 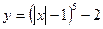 ; 2)
; 2) 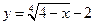 .
.
Решение. 1. Для построения графика данной функции используем правила преобразования графиков:
1) строим график функции 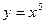 ;
;
2) график функции 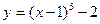 получаем из графика функции
получаем из графика функции 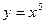 путем движения его на 1 единицу вправо по оси
путем движения его на 1 единицу вправо по оси 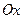 и на 2 единицы вниз по оси
и на 2 единицы вниз по оси 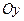 ;
;
3) график исходной функции получаем из графика функции 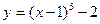 : оставляем часть графика, которая находится справа от оси
: оставляем часть графика, которая находится справа от оси 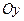 и на оси
и на оси 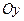 , остальную отбрасываем, а оставшуюся часть отображаем симметрично оси
, остальную отбрасываем, а оставшуюся часть отображаем симметрично оси 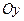 (рис.8).
(рис.8).
Рис. 8
2. Преобразуем функцию к виду 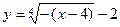 . Заметим, что
. Заметим, что 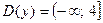 . График этой функции получаем путем следующих преобразований:
. График этой функции получаем путем следующих преобразований:
1) строим график функции 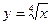 ;
;
2) график 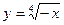 получаем из предыдущего симметричным отображением относительно оси
получаем из предыдущего симметричным отображением относительно оси 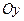 ;
;
3) график функции 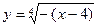 получаем из предыдущего смещением на 4 единицы вправо по оси
получаем из предыдущего смещением на 4 единицы вправо по оси 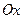 ;
;
4) график заданной функции получаем из графика функции 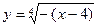 параллельным переносом его на 2 единицы вниз по оси
параллельным переносом его на 2 единицы вниз по оси 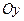 (рис.9).
(рис.9).
Рис. 9
Задания
I уровень
1.1. Определите, принадлежит ли точка 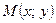 графику функции
графику функции 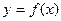 :
:
1) 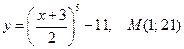 ;
;
2) 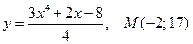 ;
;
3) 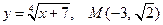 ;
;
4) 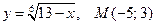
1.2. Найдите область определения функции:
1) 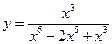 ; 2)
; 2) 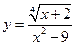 ;
;
3) 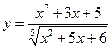 ; 4)
; 4) 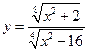 .
.
1.3. Постройте график функции и определите область ее значений:
1) 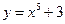 ; 2)
; 2) 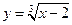 ;
;
3) 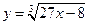 ; 4)
; 4) 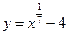 .
.
II уровень
2.1. Найдите область определения функции:
1) 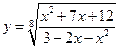 ; 2)
; 2) 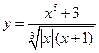 ;
;
3) 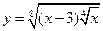 ; 4)
; 4) 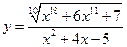 ;
;
5) 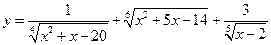 .
.
2.2. Постройте график функции:
1) 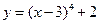 ; 2)
; 2) 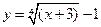 ;
;
4) 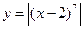 ; 4)
; 4) 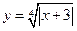 .
.
III уровень
3.1. Найдите область определения функции:
1) 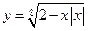 ; 2)
; 2) 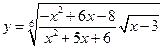 ;
;
3) 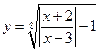 ; 4)
; 4) 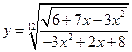 .
.
3.2. Найдите функцию, обратную данной. Укажите область определения и область значений обеих функций. постройте графики данной функции и обратной в одной системе координат:
1) 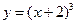 ; 2)
; 2) 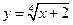 .
.
3.3. Найдите множество значений функции:
1) 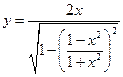 ; 2)
; 2) 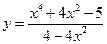 .
.
Дата добавления: 2016-07-27; просмотров: 4516;











