Функция, ее свойства и график

Пусть X и Y некоторые числовые множества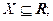

Если каждому 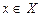по некоторому правилу f ставится в соответствие единственный элемент 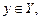то говорят, что задана функция.

Обозначается

где х – аргумент или независимая переменная функции;

у – значение функции или зависимая переменная.

Множество Х значений независимой переменной называется областью определения функции и обозначается 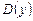или

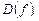
Множество всех значений зависимой переменной Y называется множеством значений функции и обозначается 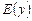или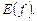

Частное значение функции 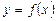при заданном частном значении аргумента 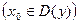обозначается .

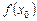Отметим особенности отыскания области определения некоторых функций:

1) область определения 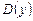дробно-рациональной функции

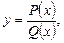
где P(x), Q(x) – некоторые многочлены, определяется условием:

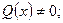
2) если аналитическое выражение функции содержит квадратный корень, т.е. задана функция 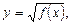то

.

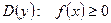В случае задания функции формулой ее область определения 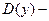это ОДЗ выражения .

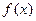Графиком функции 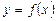называется множество всех точек плоскости с координатами 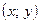, где .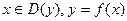

Способы задания числовой функции:

1) табличный – указываются значения переменной х и соответствующие им значения переменной y, составляется таблица

2) аналитический – указывается область определения функции 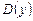и задается формула, по которой каждому значению ставится в соответствие ;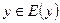

3) графический– задается график функции.

Свойства функции.