Таким образом, по способу получения относительные величины всегда вторичны.
Относительные величины, получаемые при сопоставлении абсолютных величин, могут быть названы относительными величинами первого порядка, а полученные при сопоставлении относительных же величин – величинами высших (второго, третьего и т.д.) порядков.
Величина, находящаяся в числителе называется сравниваемой. Величина, находящаяся в знаменателе называется базой сравнения или основанием.
Для выражения результата сопоставления одноименных величин используется:
- коэффициенты, если база сравнения принимается за единицу;
- проценты, %, если база сравнения принимается за сто;
- промилле, ‰, если база сравнения принимается за тысячу;
- продецимилле, если база сравнения принимается за десять тысяч.
Проценты используются в тех случаях, когда сравниваемый абсолютный показатель превосходит базисный не более чем в 2-3 раза (или базисный превосходит сравниваемый не более чем в 100 раз, например 174% или 5%). Проценты свыше 200-300 обычно заменяются коэффициентом, так 470% - 4,7 раза.
Если базисный показатель превышает сравниваемый более чем в 100 раз, но менее чем в 1000 удобно использовать промилле (тысячную долю). Широко применяется в статистике населения: показатели рождаемости, смертности, брачности и т.п.
Численность студентов ВУЗов, врачей и т.п. обычно определяется в расчете на 10000 человек, т.е. с использованием продецимилле.
При сопоставлении разноименных величин результат выражается сочетаниями наименований сравниваемых величин:
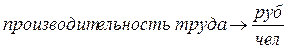 ,
, 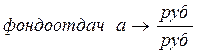 ,
, 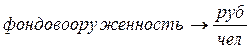 и т.д.
и т.д.
Выделяют 7 видов относительных величин:
1. Относительная величина динамики (ОВД) –характеризует изменение во времени:
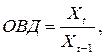
где Хt, Хt-1 – текущий и предыдущий уровень некоторого показателя.
2. Относительная величина плана (прогноза) (ОВП) – характеризует планируемое (прогнозируемое) изменение показателя:
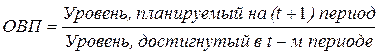 .
.
3. Относительная величина реализации плана (ОВРП) – характеризует изменение фактического (достигнутого) уровня по сравнению с планом:
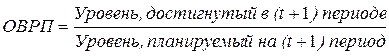
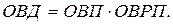
Пусть фирма планировала увеличить товарооборот в 1,4 раза, или на 40%, с 2,0 млн. руб. до 2,8 млн. руб. Следовательно, 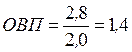 . Однако, товарооборот фирмы возрос лишь до 2,6 млн. руб., т.е. план был реализован на 92,9%:
. Однако, товарооборот фирмы возрос лишь до 2,6 млн. руб., т.е. план был реализован на 92,9%: 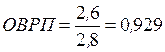 . Таким образом, товарооборот фирмы возрос в 1,3 раза или на 30% по сравнению с 2006 г.:
. Таким образом, товарооборот фирмы возрос в 1,3 раза или на 30% по сравнению с 2006 г.: 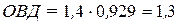 .
.
4. Относительная величина структуры (ОВС) – характеризует структуру совокупности и показывает, какую долю (или удельный вес) во всей совокупности составляет отдельная ее часть (например, удельный вес женщин, мужчин, малых предприятий, частных предприятий):
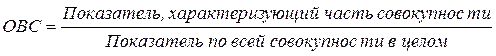 .
.
5. Относительная величина координации (ОВК) – характеризует соотношение между отдельными частями одной совокупности:
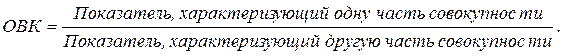
6. Относительная величина интенсивности и уровня экономического развития (ОВИ) – характеризует степень распространения или развития какого-либо явления в определенной среде:
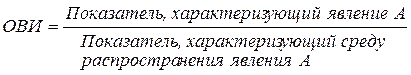 .
.
Эта величина определяется сопоставлением разноименных, но связанных между собой абсолютных величин (например, фондоотдача, фондоемкость, плотность населения на один кв. км)
7) Относительная величина сравнения (ОВСр) – характеризует изменение в пространстве.
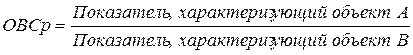 .
.
Научная ценность относительных показателей высока, но их нельзя рассматривать в отрыве от абсолютных показателей, соотношения которых они выражают, иначе они не смогут точно характеризовать изучаемые явления. Пользуясь в анализе относительными величинами, необходимо показать, какие абсолютные показатели за ними скрываются.
Метод средних величин
Средняя – это один из распространенных приемов обобщения.
Средней величиной в статистике называется обобщающая количественная характеристика признака в статистической совокупности, отражающая типичный уровень этого признака в расчете на единицу совокупности.
Существуют различные категории средних величин. Наиболее распространены степенные средние и структурные средние (мода, медиана).
Степенные средние. Веса усреднения
Математическая статистика выводит различные средние из формулы степенной средней:
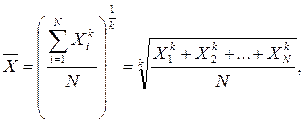
где k - показатель степени, определяющий вид степенной средней.
С изменением показателя степени k формула степенной средней меняется, и в каждом отдельном случае приходим к определенному виду средней (гармонической, геометрической, арифметической, квадратической и т.д.).
При расчете средней по данной формуле предполагается, что все значения усредняемого признака Х имеют одинаковую важность (вес). Она называется простой степенной средней. Если же значения Х имеют неодинаковую важность (вес) при усреднении, то в формулу степенной средней вводится дополнительный показатель – вес усреднения - fi. В результате получаем формулу взвешенной степенной средней:
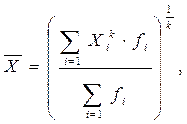
где fi - вес усреднения.
Величина средней взвешенной зависит уже не только от величины индивидуальных значений признака (как в простой средней), но и от соотношения весов. Например, чем больше веса у малых значений вариант, тем величина средней меньше. Поэтому важное значение имеет обоснование и выбор веса.
Средняя арифметическая. Гармоническая, геометрическая и квадратическая средние
Показатель степени k в формуле степенной средней определяет вид степенной средней. При k = -1 имеем гармоническую среднюю; при k = 0 - среднюю геометрическую; k = 1 - среднюю арифметическую; k =2 - среднюю квадратическую. Формулы расчета и области применения различных видов степенных средних приведены в табл. 3.1.
Таблица 3.1
Виды степенных средних
| k | Название средней | Формула расчета средней | Область применения | |
| Простая | Взвешенная | |||
| -1 | Гармоническая | 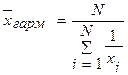
| 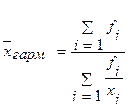
| Усреднение относительных величин (за исключением относительных показателей динамики) |
| Арифметическая | 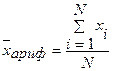
| 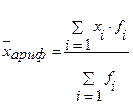
| Усреднение абсолютных, относительных величин (за исключением относительных показателей динамики) | |
| Квадратическая | 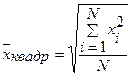
| 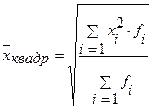
| Например, для вычисления средней величины стороны n квадратных участков, средних диаметров n труб, стволов и т.п., при построении показателя вариации |
Известно, что степенные средние разных видов, исчисленные по одной и той же совокупности, имеют различные количественные значения. Свойство мажорантности степенных средних заключается в следующем: чем больше показатель степени k, тем больше величина соответствующей степенной средней (данное утверждение справедливо для совокупности с положительными значениями признака Х). Т.е.:
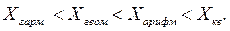
Свойства средней арифметической
Наиболее распространенным видом степенной средней является средняя арифметическая. Она обладает рядом свойств.
Сущностные свойства:
1. Средняя арифметическая постоянной величины равна этой постоянной.
2. Алгебраическая сумма линейных отклонений (разностей) индивидуальных значений признака от средней арифметической равно нулю: 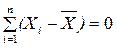 .
.
3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической есть величина минимальная:
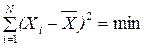
или
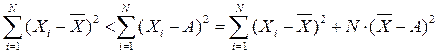
где А - константа.
Вычислительные свойства:
1. если все значения признака уменьшить (увеличить) на одну и ту же величину А, то и средняя арифметическая уменьшится (увеличится) на ту же самую величину А;
2. если все значения признака разделить (умножить) на какое-либо постоянное число А, то средняя арифметическая уменьшится (увеличится) в А раз;
3. если вес каждого значения признака разделить на какое-либо постоянное число А, то средняя арифметическая не изменится.
Понятие ведущего показателя
Категорию средней величины можно раскрыть через понятие ведущего (определяющего, итогового) показателя.
Ведущий показатель - это существенная характеристика совокупности как целого, определяемая всеми единицами этой совокупности: W = f(X1, X2, ..., XN). Она обладает следующим свойством: при замене индивидуальных значений признака в формуле расчета W их средней величиной, величина ведущего показателя не меняется, т.е.:
f(X1, X2, ..., XN ) = f( 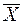 ,
, 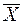 ,... ,
,... , 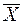 ).
).
В большинстве случаев ведущий показатель имеет реальный экономический смысл. Формулы расчета ведущих показателей в зависимости от вида степенной средней приведены в табл. 3.2.
Таблица 3.2.
Формулы расчета ведущих показателей
| Вид степенной средней | Ведущий показатель | Вид степенной средней | Ведущий показатель |
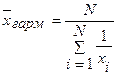
| 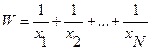
| 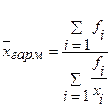
| 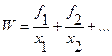
|
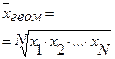
| 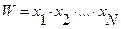
| 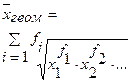
| 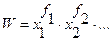
|
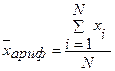
| 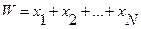
| 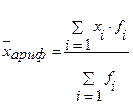
| 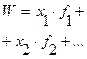
|
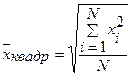
| 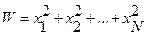
| 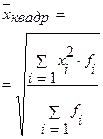
| 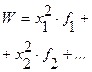
|
Обусловленность способа усреднения характером статистического материала
Применение конкретной формы средней величины зависит от вида усредняемого признака Х (абсолютная, средняя или относительная величина) и от того, в каком виде представлены исходные данные. При выборе вида средней величины обычно исходят из логической сущности усредняемого признака и его взаимосвязи с ведущим показателем. Величина ведущего показателя не должна изменяться при замене индивидуальных значений признака средней величиной.
Для усреднения абсолютных величин применяется средняя арифметическая. В случае несгруппированных данных используют простую среднюю арифметическую. А если данные сгруппированы, то применяют среднюю арифметическую взвешенную. При этом в качестве весов усреднения используют:
- частота повторения (число единиц) или доля единиц (частость) для дискрентных и равноинтеравльных рядов распределения;
- плотность распределения для неравноинтервальных рядов.
Усреднение относительных показателей
Если требуется найти среднее значение относительного показателя x, представляющего собой отношение абсолютных показателей (y и z): x=y/z, то используют формулу: 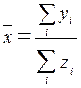 . Отсюда следует, что средняя из относительных величин есть относительная величина, рассчитанная по совокупности в целом (т.к.
. Отсюда следует, что средняя из относительных величин есть относительная величина, рассчитанная по совокупности в целом (т.к. 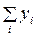 – суммарное значение признака y для всей совокупности;
– суммарное значение признака y для всей совокупности; 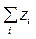 – суммарное значение признака z для всей совокупности).
– суммарное значение признака z для всей совокупности).
В зависимости от имеющихся данных формула расчета среднего значения x может быть сведена к формуле среднего арифметического взвешенного либо среднего гармонического взвешенного.
Когда имеются данные об индивидуальных значениях относительного показателя x и индивидуальных значениях абсолютного показателя знаменателя - z в совокупности, то значения показателя y могут быть вычислены как: y=z·x и формула расчета 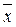 будет иметь вид:
будет иметь вид: 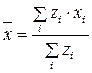 . Это формула среднего арифметического взвешенного, где xi - усредняемые значения показателя, zi - веса усреднения.
. Это формула среднего арифметического взвешенного, где xi - усредняемые значения показателя, zi - веса усреднения.
Когда имеются данные об индивидуальных значениях относительного показателя x и абсолютного показателя числителя - y, то значения показателя z могут быть вычислены как: z=y/x и формула расчета 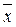 будет иметь вид:
будет иметь вид: 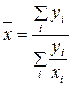 . Это формула среднего гармонического взвешенного, где xi - усредняемые значения показателя, yi - веса усреднения.
. Это формула среднего гармонического взвешенного, где xi - усредняемые значения показателя, yi - веса усреднения.
Например, на основе имеющихся данных (табл. 3.3) определить среднюю долю (процент) студентов потока, совмещающих учебу с работой.
Таблица 3.3
Данные о проценте и числе работающих студентов
по группам потока
| N группы | Доля (процент) работающих студентов (x, %) | Число работающих студентов, чел. (y) |
| Итого | - |
Расчет средней доли работающих студентов выражается соотношением:
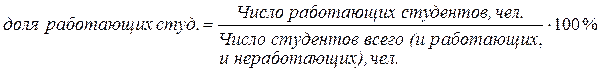
Число работающих студентов известно, а число студентов всего нет. Однако, мы можем рассчитать его как частное от деления числа работающих студентов на долю. Тогда средняя доля работающих студентов по трем группам может быть рассчитана по формуле средней гармонической взвешенной:
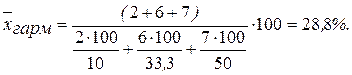
Этот же результат получится и по формуле средней арифметической взвешенной, если в качестве весов принять число студентов всего (чел.), который необходимо предварительно рассчитать:
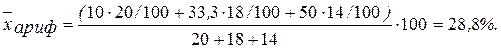
Расчет по формуле средней гармонической взвешенной избавляет от предварительного расчета весов, поскольку эта операция заложена в саму формулу.
Показатели центра распределения: средняя арифметическая, медиана, мода. Методы их расчета для различных видов рядов распределения
Показатели центра распределения позволяют определить типичное значение признака в совокупности:
- Средняя арифметическая
В случае несгруппированных данных используют простую среднюю арифметическую:
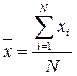 ,
,
где xi – значение признака у i–ой единицы совокупности;
N - объем совокупности.
В случае сгруппированных данных применяется средняя арифметическая взвешенная:
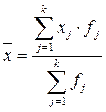 ,
,
где xj –значение признака в j–ой группе (j=1;k);
k – число групп;
fj – вес усреднения для j-ой группы (в качестве весов усреднения берут частоты/частости).
Если значение признака в группе задано интервалом, то в качестве варианты xj берется середина интервала (центральное значение):
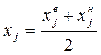 ,
,
где хнj, хвj - нижняя и верхняя граница интервала.
Иногда приходится рассчитывать общую среднюю по групповым средним - 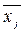 (по средним отдельных частей совокупности). В этом случае групповые средние принимаются как варианты, а расчет производят по формуле средней арифметической взвешенной:
(по средним отдельных частей совокупности). В этом случае групповые средние принимаются как варианты, а расчет производят по формуле средней арифметической взвешенной:
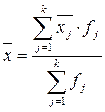 .
.
- Структурные характеристики распределения: квантили распределения и мода
К структурным характеристикам ряда распределения относят квантили распределения (медиану, квартили, децили и др.) и моду.
Квантили распределения представляют собой обобщающие показатели, характеризующие структуру распределения признака в совокупности.
Квантиль распределения– это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности.
Виды квантилей:
1) медиана (Ме) - значение признака, приходящееся на середину упорядоченной совокупности,
2) квартили (Q1/4, Q2/4=Ме, Q3/4) – значения признака, делящие упорядоченную совокупность на 4 равные (по числу единиц) части,
3) децили (Q0,1,Q0,2,…,Q0,9) – значения признака, делящие упорядоченную совокупность на 10 равных частей,
4) перцентили (Q0,01,Q0,02,…,Q0,99) - значения признака, делящие упорядоченную совокупность на 100 равных частей.
Например, по данным о 12 предприятий розничной торговли требуется определить медиану и квартили для признака х – объем продаж за период, тыс. усл. ден. ед.
Упорядочим совокупность по х (табл. 3.4). В совокупности 12 единиц. Середина приходится на 6 и 7 элементы, значения признака у которых 31 и 32 соответственно. Медианой будет среднее из значений этих элементов:
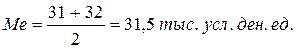
Таблица 3.4
Определение медианы и квартилей по несгруппированным данным
| Х |
Q1/4 Q2/4=Ме Q3/4
Первый квартиль отделяет первую четверть элементов совокупности (т.е. 3 единицы). Его значение будет равно среднему из значений признака у 3-его и 4-ого элементов, т.е.
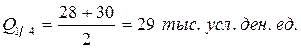
Третий квартиль отделяет последнюю четверть элементов совокупности. Его значение будет равно среднему из значений признака у 9-го и 10-го элементов, т.е.
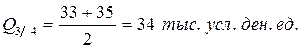
Если данные сгруппированы, то значение квантиля определяется по накопленным частотам. При этом определяется номер группы, которая содержит i-ый квантиль, как номер первой группы от начала ряда, в которой сумма накопленных частот равна или превышает N·i, где i- индекс квантиля.
Если ряд интервальный, то значение квантиля уточняется по формуле:
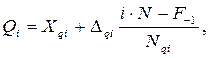
где Xqi - нижняя граница интервала, в котором находится i - ый квантиль;
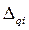 - величина интервала, в котором находится i - ый квантиль;
- величина интервала, в котором находится i - ый квантиль;
F(-1) – сумма накопленных частот интервалов, предшествующих интервалу, в котором находится i - ый квантиль;
Nqi – частота интервала, в котором находится i - ый квантиль.
Пусть, требуется определить медиану и квартили распределения признака х – объем продаж по данным равноинтервальной группировки (табл. 3.5).
Таблица 3.5
Определение медианы и квартилей по сгруппированным данным
| № группы j | Объем продаж за период (хн j; х вj) | Количество предприятий (частота) Nj | Накопленная частота Fj (сравнивается с N∙0,5 = 6) |
| [26 ; 30) | 3 ≥ 6 (ЛОЖЬ) | ||
| [30 ; 34) Ме, Мо | 9 ≥ 6 (ИСТИНА) | ||
| [34 ; 38) | |||
| ИТОГО |
Определим номер группы, содержащей Ме. Это будет 2-ая группа, т.к. накопленная частота в этой группе равна 9, что больше N·0,5=12·0,5=6.
Теперь уточним значение Ме по формуле для определения квантилей в интервальном ряду:
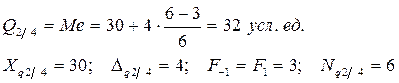
Значение медианы можно определить графически по кумуляте. Для этого максимальную ординату кумуляты делят пополам. И через полученное значение проводят линию параллельную горизонтальной оси. Абсцисса точки пересечения этой линии и кумуляты дает значение медианы, совпадет со значением, полученным при расчете по сгрупированным данным.
Наиболее распространенным видом квантилей является медиана. Медиана не требует знания всех индивидуальных значений признака. Она не чувствительна к крайним значениям признака, которые могут резко отличаться от основной массы его значений. Поэтому медиану используют как наиболее надежный показатель типичного значения признака в неоднородной совокупности (включающей резкие отклонения от 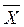 ).
).
Медиана находит практическое применение также вследствие особого математического свойства - свойства минимальности. Согласно данному свойству сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая:
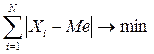 .
.
Мода (Мо) – наиболее часто встречающееся значение признака в совокупности.
Для дискретного ряда мода – это значение признака, которому соответствует наибольшая частота (частость) распределения. Для интервального ряда – это значение признака, которому соответствует наибольшая плотность распределения. Если ряд равноинтервальный, то значение моды можно определить по частотам (частостям): их соотношение будет таким же, что и плотностей распределения. Кроме того, значение моды в случае равноинтервального ряда можно уточнить по формуле:
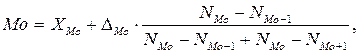
где XMo - нижняя граница интервала, в котором находится мода;
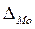 - величина модального интервала;
- величина модального интервала;
NMо, NMо-1, NMо+1 – частоты, соответственно, модального, предшествующего и последующего интервалов.
Пусть, требуется определить моду для распределения признака объем продаж, используя данные равноинтервальной группировки (табл. 3.5).
Модальным будет 2-ой интервал [30 –34], т.к. в этом интервале наибольшая частота (NMо=6). Приближенное значение Мо определим по формуле: Мо=30+4(6-3)/(6-3+6-3)=32 (усл.ден.ед.).
Значение моды можно определить графически по гистограмме. При этом соединяют вершины самого высокого (модального) столбца с соседними вершинами так, чтобы полученные отрезки пересекались и лежали внутри данного столбца. Если соседний столбец отсутствует, вершину соединяют с противоположным основанием. Абсцисса точки пересечения дает значение моды, совпадающее со значением, полученным при расчете по сгруппированным данным.
Если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды. Если две не соседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называют бимодальным; если таких вариант больше двух, то ряд – полимодальный.
Мода также как и медиана не требует знания всех индивидуальных значений признака и поэтому может быть использована в качестве наиболее типичного значения признака в неоднородной совокупности.
Вариационный анализ. Показатели вариации и их значение в статистике
Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Однако два распределения, имеющие одинаковую среднюю арифметическую, могут значительно отличаться друг от друга по степени рассеяния (вариации) признака. Если индивидуальные значения признака ряда мало отличаются друг от друга (рис. 3.1 А), то средняя арифметическая будет достаточно надежной показательной характеристикой типичного уровня в данной совокупности. Если же ряд распределения характеризуется значительным рассеиванием индивидуальных значений признака (рис. 3.2 Б), то средняя арифметическая будет ненадежной характеристикой типичного уровня этой совокупности и ее практическое применение будет ограничено.
 А) ······´····· Х
А) ······´····· Х
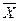
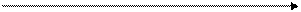 Б) · · · · · · ´ · · · · · Х
Б) · · · · · · ´ · · · · · Х
Рис. 3.1. Распределения с малой (А) и большой (Б)
вариацией.
Вариационный размах, дисперсия, коэффициент вариации. Свойства и методы расчета показателей вариации
Для измерения рассеяния (вариации) признака применяются различные абсолютные и относительные показатели вариации.
К абсолютным показателям вариации относятся:
- Размах вариации, R - разность между максимальным и минимальным значениями признака в совокупности:
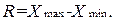
Среднее по совокупности отклонение индивидуального значения признака от его среднего уровня измеряют два следующих показателя вариации: среднее линейное и среднее квадратическое отклонение.
- Среднее линейное отклонение, d - представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариант от их средней арифметической (при этом всегда полагают, что среднюю вычитают из варианты). Для несгруппированных и сгруппированных данных, соответственно:
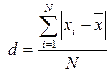 ,
, 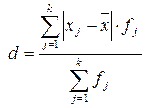 ,
,
где N – объем совокупности;
k - число групп;
fj – частота/частость в j – ой группе.
Математические свойства модулей плохие, поэтому часто на практике применяют другой показатель среднего отклонения от средней - среднеее квадратическое отклонение.
- Среднее квадратическое отклонение, s - представляет собой среднюю квадратическую из отклонений отдельных вариант от их средней арифметической. Для несгруппированных и сгруппированных данных, соответственно:
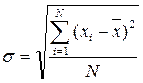 ,
, 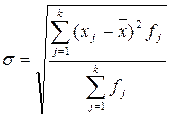 .
.
- Дисперсия, s2 - это квадрат среднего квадратического отклонения. Она представляет собой средний квадрат отклонений вариант от их средней величины. Она может быть также вычислена, как разность среднего квадрата значения признака и квадрата среднего арифметического значения признака:
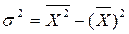 .
.
Среднее квадратическое отклонение наряду с дисперсией входят в большинство теорем теории вероятности и математической статистики, что обусловливает их широкое применение на практике. Кроме того, дисперсия может быть разложена на составные части, позволяющие оценить влияние различных факторов, обусловливающих вариацию признака.
Теорема (правило) о разложении дисперсии при группировании. Пусть при группировке совокупности по некоторому признаку Х было образовано k однородных групп. Согласно теореме общая дисперсия признака Х (по совокупности в целом) может быть разложена на две составные части: 1) межгрупповую и 2) остаточную (среднюю из внутригрупповых) дисперсии:
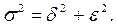
Общая дисперсия рассчитывается по формуле простой дисперсии и показывает величину вариации признака, обусловленную всеми факторами, влияющими на данный признак.
Межгрупповая дисперсия, 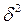 - характеризует ту часть общей вариации признака, которая обусловлена делением совокупности на группы. Если деление совокупности на группы обусловлено факторами, влияющими на интересующий нас признак, то данную дисперсию называют еще факторной дисперсией. Межгрупповая дисперсия равна среднему взвешенному квадрату отклонений групповых (частных) средних
- характеризует ту часть общей вариации признака, которая обусловлена делением совокупности на группы. Если деление совокупности на группы обусловлено факторами, влияющими на интересующий нас признак, то данную дисперсию называют еще факторной дисперсией. Межгрупповая дисперсия равна среднему взвешенному квадрату отклонений групповых (частных) средних 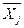 от общей средней
от общей средней 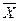 :
:
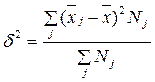 ,
,
где Nj- численность единиц в j - ой группе.
Средняя из внутригрупповых (или остаточная) дисперсия, 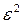 - характеризует остаточную вариацию, несвязанную с группированием. То есть, характеризует вариацию признака, обусловленную прочими факторами, не связанными с делением совокупности на группы. Вычисляется она как средняя взвешенная из внутригрупповых дисперсий:
- характеризует остаточную вариацию, несвязанную с группированием. То есть, характеризует вариацию признака, обусловленную прочими факторами, не связанными с делением совокупности на группы. Вычисляется она как средняя взвешенная из внутригрупповых дисперсий:
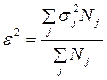 ,
,
где sj2 - дисперсия признака внутри j–ой группы.
Применение теоремы о разложении дисперсии.
1. Межгрупповую (или остаточную) дисперсию используют в качестве критерия группирования для группировок с одинаковым числом групп. Очевидно, что чем больше межгрупповая дисперсия d2, тем лучше проведена группировка (выделенные при группировки группы сильнее различаются между собой). Лучшей будет та группировка, у которой величина d2 больше (или e2 меньше).
2. Пользуясь теоремой сложения дисперсий, можно всегда по двум известным дисперсиям отыскать третью – неизвестную, а также судить о силе влияния группировочного признака.
В случае аналитической группировки, теорема о разложении дисперсии позволяет через межгрупповую дисперсию оценить влияние признака-фактора (х) на вариацию признака-результата (y) с помощью показателя – эмпирического корреляционного отношения (см. тему 4).
Основные вычислительные свойства дисперсии:
1. дисперсия постоянной величины равна 0;
2. если все варианты значений признака уменьшить на одно и то же число, то дисперсия не изменится;
3. если все варианты значений признака уменьшить в одно и то же число А раз (А-const), то дисперсия уменьшится в А2 раз.
Относительные показатели вариации применяют, если необходимо оценить интенсивность вариации, или сравнить вариацию признака в различных совокупностях, или сравнить вариацию различных признаков. Показатель относительной вариации рассчитывается как отношение абсолютного показателя вариации к среднему значению.
Самым распространенным относительным показателем рассеяния является коэффициент вариации. Он представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
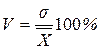 .
.
Коэффициент вариации используют также как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.
Показатели формы распределения: показатели асимметрии и характеристики эксцесса распределения
Для характеристики однородности совокупности помимо показателей вариации можно использовать показатели формы распределения: коэффициент асимметрии и эксцесс.
Коэффициент асимметрии, As-показатель симметричности распределения. Симметричнымявляется распределение, в котором частоты любых двух вариант, равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричных одновершинных распределений средняя арифметическая, мода и медиана равны между собой. Положительная величина показателя асимметрии указывает на наличие правосторонней асимметрии, отрицательная – на наличие левосторонней асимметрии (рис. 3.2.). Близость нулю показателя асимметрии свидетельствует о симметричном распределении.


 As<0 As>0
As<0 As>0
 |  |
а) б)
Рис. 3.2. Виды асимметрии: а) левосторонняя; б) правосторонняя
Существуют различные способы расчета коэффициента асимметрии:
1. Коэффициент асимметрии Пирсона:
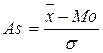 .
.
Величина As может изменяться от –1 до +1 (для одновершинных распределений). Чем ближе по модулю As к 1, тем асимметрия существеннее.
2. Наиболее точным и распространенным является показатель, основанный на определении центрального момента третьего порядка – М3:
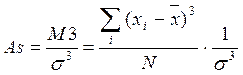 .
.
В симметричном распределении его величина равна нулю. Для оценки существенности такого коэффициента асимметрии вычисляется показатель средней квадратической ошибки коэффициента асимметрии:
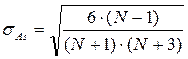 ,
,
где N - объем совокупности.
Отношение çAsç/sAs, дающее значение меньше 2, свидетельствует о несущественном характере асимметрии.
Коэффициент эксцесса, Ex-показатель островершинности распределения. Он рассчитывается для симметричных распределений.Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Наиболее точным является показатель, использующий центральный момент четвертого порядка - М4:
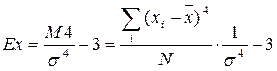 .
.

 Для нормального распределения отношение М4/s4=3, следовательно эксцесс равен нулю. Наличие положительного эксцесса означает, что распределение более островершинное чем нормальное; отрицательное значение эксцесса означает более плосковершинный характер распределения, чем у нормального (рис. 3.3.).
Для нормального распределения отношение М4/s4=3, следовательно эксцесс равен нулю. Наличие положительного эксцесса означает, что распределение более островершинное чем нормальное; отрицательное значение эксцесса означает более плосковершинный характер распределения, чем у нормального (рис. 3.3.).
 Ex>0
Ex>0
 Ex=0
Ex=0
Ex<0
Рис. 3.3. Эксцесс распределения.
Для оценки существенности коэффициента эксцесса вычисляется показатель средней квадратической ошибки коэффициента эксцесса:
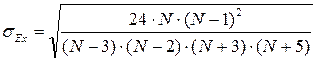 ,
,
где N - объем совокупности.
Отношение çExç/sEx, дающее значение меньше 2, свидетельствует о несущественном характере эксцесса (близости распределения по характеру островершинности к нормальному).
Контрольные вопросы
Дата добавления: 2020-10-25; просмотров: 524;











