Начисление процентов. Расчет наращенной стоимости

В условиях рыночной экономики любое взаимодействие лиц, фирм и предприятий с целью получения прибыли называется сделкой. При кредитных сделках прибыль представляет собой величину дохода от предоставления денежных средств в долг, что на практике реализуется за счет начисления процентов (процентной ставки – i). Проценты зависят от величины предоставляемой суммы, срока ссуды, условий начисления и т. д.

Важнейшее место в финансовых сделках занимает фактор времени (t). С временным фактором связан принцип неравноценности и неэквивалентности вложений. Для того чтобы определить изменения, происходящие с исходной суммой денежных средств (P), необходимо рассчитать величину дохода от предоставления денег в ссуду, вложения их в виде вклада (депозита), инвестированием их в ценные бумаги и т. д.

Процесс увеличения суммы денег в связи с начислением процентов (i) называют наращением, или ростом первоначальной суммы (P). Таким образом, изменение первоначальной стоимости под влиянием двух факторов: процентной ставки и времени называется наращенной стоимостью (S).

Наращенная стоимость может определяться по схеме простых и сложных процентов. Простые проценты используются в случае, когда наращенная сумма определяется по отношению к неизменной базе, то есть начисленные проценты погашаются (выплачиваются) сразу после начисления (таким образом, первоначальная сумма не меняется); в случае, когда исходная сумма (первоначальная) меняется во временном интервале, имеют дело со сложными процентами.

При начислении простых процентов наращенная сумма определяется по формуле

S = P (1 + i t), (1)

где S – наращенная сумма (стоимость), руб.; P – первоначальная сумма (стоимость), руб.; i – процентная ставка, выраженная в коэффициенте; t – период начисления процентов.

Пример 1

Рассчитать сумму начисленных процентов и сумму погашения кредита, если выдана ссуда в размере 10 000 руб., на срок 1 год при начислении простых процентов по ставке 13 % годовых.

Решение

S = 10 000 (1+ 0,13 · 1) = 11 300, руб. (сумма погашения кредита);

ΔР = 11 300 – 10 000 = 1 300, руб. (сумма начисленных процентов).

Пример 2

Определить сумму погашения долга при условии ежегодной выплаты процентов, если банком выдана ссуда в сумме 50 000 руб. на 2 года, при ставке – 16 % годовых.

Решение

S = 50 000 (1+ 0,16 · 2) = 66 000, руб.

Таким образом, начисление простых процентов осуществляется в случае, когда начисленные проценты не накапливаются на сумму основного долга, а периодически выплачиваются, например, раз в год, полугодие, в квартал, в месяц и т. д., что определяется условиями кредитного договора. Также на практике встречаются случаи, когда расчеты производятся за более короткие периоды, в частности на однодневной основе.

В случае, когда срок ссуды (вклада и т. д.) менее одного года, в расчетах необходимо скорректировать заданную процентную ставку в зависимости от временного интервала. Например, можно представить период начисления процентов (t) в виде отношения 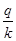, где q – число дней (месяцев, кварталов, полугодий и т. д.) ссуды; k – число дней (месяцев, кварталов, полугодий и т. д.) в году.

Таким образом, формула (1) изменяется и имеет следующий вид:

S = P (1 + i 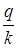). (2)

Пример 3

Банк принимает вклады на срочный депозит на срок 3 месяца под 11 % годовых. Рассчитать доход клиента при вложении 100 000 руб. на указанный срок.

Решение

S = 100 000 (1+ 0,11 · 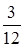) = 102 749,9, руб.;

ΔР = 102 749,9 – 100 000 = 2 749,9, руб.

В зависимости от количества дней в году возможны различные варианты расчетов. В случае, когда за базу измерения времени берут год, условно состоящий из 360 дней (12 месяцев по 30 дней), исчисляют обыкновенные, или коммерческие проценты. Когда за базу берут действительное число дней в году (365 или 366 – в високосном году), говорят о точных процентах.

При определении числа дней пользования ссудой также применяется два подхода: точный и обыкновенный. В первом случае подсчитывается фактическое число дней между двумя датами, во втором – месяц принимается равным 30 дням. Как в первом, так и во втором случае, день выдачи и день погашения считаются за один день. Также существуют случаи, когда в исчислении применяется количество расчетных или рабочих банковских дней, число которых в месяц составляет 24 дня.

Таким образом, выделяют четыре варианта расчета:

1) обыкновенные проценты с точным числом дней ссуды;

2) обыкновенные проценты с приближенным числом дней ссуды;

3) точные проценты с приближенным числом дней ссуды;

4) точные проценты с банковским числом рабочих дней.

При этом необходимо учесть, что на практике день выдачи и день погашения ссуды (депозита) принимают за один день.

Пример 4

Ссуда выдана в размере 20 000 руб. на срок с 10.01.06 до 15.06.06 под 14 % годовых. Определить сумму погашения ссуды.

Решение

1. Обыкновенные проценты с точным числом дней ссуды:

156=21+28+31+30+31+15;

S = 20 000 (1+0,14 · 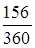) =21 213,3, руб.

2. Обыкновенные проценты с приближенным числом дней ссуды:

155= (30·5)+5

S = 20 000 (1+0,14 · ) =21 205,6, руб.

3. Точные проценты с приближенным числом дней ссуды:

S = 20 000 (1+0,14 · ) =21 189,0, руб.

4. Точные проценты с банковским числом рабочих дней:

S = 20 000 (1+0,14 · 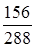) =21 516,7, руб.

Данные для расчета количества дней в периоде представлены в прил. 1, 2.

Как сказано выше, кроме начисления простых процентов применяется сложное начисление, при котором проценты начисляются несколько раз за период и не выплачиваются, а накапливаются на сумму основного долга. Этот механизм особенно эффективен при среднесрочных и долгосрочных кредитах.

После первого года (периода) наращенная сумма определяется по формуле (1), где i будет являться годовой ставкой сложных процентов. После двух лет (периодов) наращенная сумма S₂ составит:

S₂ = S₁(1 + it) = P (1 + it) · (1 + it) = P (1 + it)².

Таким образом, при начислении сложных процентов (после n лет (периодов) наращения) наращенная сумма определяется по формуле

S = P (1 + i t)ⁿ , (3)

где i – ставка сложных процентов, выраженная в коэффициенте; n – число начислений сложных процентов за весь период.

Коэффициент наращения в данном случае рассчитывается по формуле

Кн = (1 + i t)ⁿ , (4)

где Кн – коэффициент наращения первоначальной стоимости, ед.

Пример 5

Вкладчик имеет возможность поместить денежные средства в размере 75 000 руб. на депозит в коммерческий банк на 3 года под 10 % годовых.

Определить сумму начисленных процентов к концу срока вклада, при начислении сложных процентов.

Решение

S = 75 000 (1+ 0,1 · 1)³ = 99 825, руб.

ΔР = 24 825, руб.

Таким образом, коэффициент наращения составит:

Кн = (1+ 0,1 · 1)³ = 1,331

Следовательно, коэффициент наращения показывает, во сколько раз увеличилась первоначальная сумма при заданных условиях.

Доля расчетов с использованием сложных процентов в финансовой практике достаточно велика. Расчеты по правилу сложных процентов часто называют начисление процентов на проценты, а процедуру присоединения начисленных процентов – их реинвестированием или капитализацией.

Рис. 1. Динамика увеличения денежных средств при начислении простых и сложных процентов

Из-за постоянного роста базы вследствие реинвестирования процентов рост первоначальной суммы денег осуществляется с ускорением, что наглядно представлено на рис. 1.

В финансовой практике обычно проценты начисляются несколько раз в году. Если проценты начисляются и присоединяются чаще (m раз в год), то имеет место m-кратное начисление процентов. В такой ситуации в условиях финансовой сделки не оговаривают ставку за период, поэтому в финансовых договорах фиксируется годовая ставка процентов i, на основе которой исчисляют процентную ставку за период ( 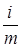). При этом годовую ставку называют номинальной, она служит основой для определения той ставки, по которой начисляются проценты в каждом периоде, а фактически применяемую в этом случае ставку (( 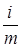)^mn) – эффективной, которая характеризует полный эффект (доход) операции с учетом внутригодовой капитализации.

Наращенная сумма по схеме эффективных сложных процентов определяется по формуле

S = P (1+ 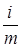)^mn , (5)

где i – годовая номинальная ставка, %; (1+ 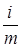)^mn – коэффициент наращения эффективной ставки; m – число случаев начисления процентов за год; mn – число случаев начисления процентов за период.

Пример 6

Рассчитать сумму выплаты по депозиту в размере 20 000 руб., помещенному на 1 год под 14 % годовых с ежеквартальным начислением процентов.

Решение

S = 20 000 (1+ 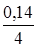)^4·1 = 22 950, руб.

Следует отметить, что при периоде, равным 1 году, число случаев начисления процентов за год будет соответствовать числу случаев начисления процентов за весь период. Если, период составляет более 1 года, тогда n (см. формулу (3)) – будет соответствовать этому значению.

Пример 7

Рассчитать сумму погасительного платежа, если выдан кредит в размере 20 000 руб. на 3 года под 14 % годовых с ежеквартальным начислением процентов.

Решение

S = 20 000 (1+ 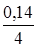)^4·3 = 31 279, 1 , руб.

Начисление сложных процентов также применяется не только в случаях исчисления возросшей на проценты суммы задолженности, но и при неоднократном учете ценных бумаг, определении арендной платы при лизинговом обслуживании, определении изменения стоимости денег под влиянием инфляции и т. д.

Как говорилось выше, ставку, которая измеряет относительный доход, полученный в целом за период, называют эффективной. Вычисление эффективной процентной ставки применяется для определения реальной доходности финансовых операций. Эта доходность определяется соответствующей эффективной процентной ставкой.

Эффективную процентную ставку можно рассчитать по формуле

I_эф = (1+ 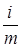)^mn – 1 . (6)

Пример 8

Кредитная организация начисляет проценты на срочный вклад, исходя из номинальной ставки 10 % годовых. Определить эффективную ставку при ежедневном начислении сложных процентов.

Решение

i = (1+ 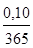)³⁶⁵ – 1 = 0,115156, т. е. 11 %.

Реальный доход вкладчика на 1 руб. вложенных средств составит не 10 коп. (из условия), а 11 коп. Таким образом, эффективная процентная ставка по депозиту выше номинальной.

Пример 9

Банк в конце года выплачивает по вкладам 10% годовых. Какова реальная доходность вкладов при начислении процентов: а) ежеквартально; б) по полугодиям.

Решение

а) i = (1+ 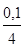)⁴ – 1 = 0,1038, т. е. 10,38 %;

б) i = (1+ 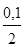)² – 1 = 0,1025, т. е. 10,25 %.

Расчет показывает, что разница между ставками незначительна, однако начисление 10 % годовых ежеквартально выгодней для вкладчика.

Расчет эффективной процентной ставки в финансовой практике позволяет субъектам финансовых отношений ориентироваться в предложениях различных банков и выбрать наиболее приемлемый вариант вложения средств.

В кредитных соглашениях иногда предусматривается изменение во времени процентной ставки. Это вызвано изменением контрактных условий, предоставлением льгот, предъявлением штрафных санкций, а также изменением общих условий совершаемых сделок, в частности, изменение процентной ставки во времени (как правило, в сторону увеличения) связано с предотвращением банковских рисков, возможных в результате изменения экономической ситуации в стране, роста цен, обесценения национальной валюты и т. д.

Расчет наращенной суммы при изменении процентной ставки во времени может осуществляться как начислением простых процентов, так и сложных. Схема начисления процентов указывается в финансовом соглашении и зависит от срока, суммы и условий операции.

Пусть процентная ставка меняется по годам. Первые n₁ лет она будет равна i₁, n₂ – i₂ и т. д. При начислении на первоначальную сумму простых процентов необходимо сложить процентные ставки i₁, i₂, i_n, а при сложных – найти их произведение.

При начислении простых процентов применяется формула

S = P (1+i₁ t₁ + i₂ t₂ + i₃ t₃ + i_n t_n) , (7)

где i_n – ставка простых процентов; t_n – продолжительность периода начисления.

Пример 10

В первый год на сумму 10 000 руб. начисляются 10 % годовых, во второй – 10,5 % годовых, в третий – 11 % годовых. Определить сумму погашения, если проценты выплачиваются ежегодно.

Решение

S = 10 000 (1+0,10 · 1 +0,105 · 1 + 0,11 · 1)=13 150, руб.;

ΔР = 3 150, руб.

При начислении сложных процентов применяется формула

S = P(1+i₁ t₁)·(1+ i₂ t₂)·(1+ i₃ t₃)·(1+ i_n t_n) (8)

где i_n – ставка сложных процентов; t_n – продолжительность периода ее начисления.

Пример 11

В первый год на сумму 10 000 руб. начисляются 10 % годовых, во второй – 10,5 % годовых, в третий – 11 % годовых. Определить сумму погашения, если проценты капитализируются.

Решение

S = 10 000 (1+0,10 · 1)·(1 +0,105 · 1)·(1 + 0,11 · 1)= 13 492, 05, руб.

Приведенные примеры подтверждают тот факт, что начисление простых процентов связано с определением наращенной суммы по отношению к неизменной базе, т. е. каждый год (период) проценты начисляются на одну и ту же первоначальную стоимость. Если рассмотреть пример 10, то в этом случае наращенная стоимость составит:

– за первый год: S₁ = 10 000 (1+0,10 · 1) = 11 000, руб.;

ΔР₁ = 1 000, руб.;

– за второй год: S₂ = 10 000 (1+0,105 · 1) = 11 050, руб.;

ΔР ₂ = 1 050, руб.;

– за третий год: S₃ = 10 000 (1+0,11 · 1) = 11 100, руб.;

ΔР ₃ = 1 100, руб.

Таким образом, сумма процентов за 3 года составит:

ΔР = 1 000+1 050+1 100 = 3 150, руб. (см. пример 10).

В случае начисления сложных процентов, исходная сумма меняется после каждого начисления, так как проценты не выплачиваются, а накапливаются на основную сумму, т. е. происходит начисление процентов на проценты. Рассмотрим пример 11:

– в первом году: S₁ = 10 000 (1+0,10 · 1) = 11 000, руб.;

– во втором году: S₂ = 11000 (1+0,105 · 1) = 12 100, руб.;

– в третьем году: S₃ = 12100 (1+0,11 · 1) = 13 431, руб.

Таким образом, сумма процентов за 3 года составит: i₃ = 3 431, руб. (см. пример 10).

При разработке условий контрактов или их анализе иногда возникает необходимость в решении обратных задач – определение срока операции или уровня процентной ставки.

Формулы для расчета продолжительности ссуды в годах, днях и т. д. можно рассчитать, преобразуя формулы (1) и (5).

Срок ссуды (вклада):

t = · 365 . (9)

Пример 12

Определить на какой срок вкладчику поместить 10 000 руб. на депозит при начислении простых процентов по ставке 10 % годовых, чтобы получить 12 000 руб.

Решение

t = ( 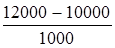) · 365 = 730 дней (2 года).

Процентную ставку можно рассчитать по формуле

i = ( 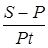). (10)

Пример 13

Клиент имеет возможность вложить в банк 50 000 руб. на полгода. Определить процентную ставку, обеспечивающую доход клиента в сумме 2 000 руб.

Решение

t = ( ) = 0,08 = 8 % годовых

Аналогично определяется необходимый срок окончания финансовой операции и ее протяженность, либо размер требуемой процентной ставки при начислении сложных процентов.

Для упрощения расчетов значения коэффициента (множитель) наращения представлены в прил. 3.