Axial moment of inertia

The axial moment of inertia about any axis in the plane of the figure is called the sum of the products of the elemental area and the square of the distance from the element and axis (Fig. 3.1).

Let us denote the moment of inertia by I with the index corresponding to the axis:

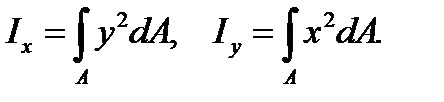(3.8)

It is evident that the axial and the polar moments are expressed in the same units –the unit of length.

The axial moment is always positive and it is not equal to zero.

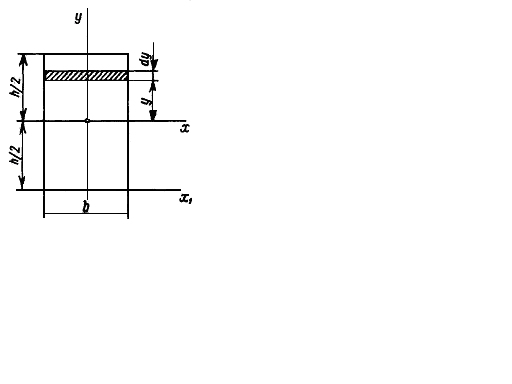
Fig. 3.3.

The sum of the axial moments about two mutually perpendicular axes is equal to the polar moment of inertia about the origin:

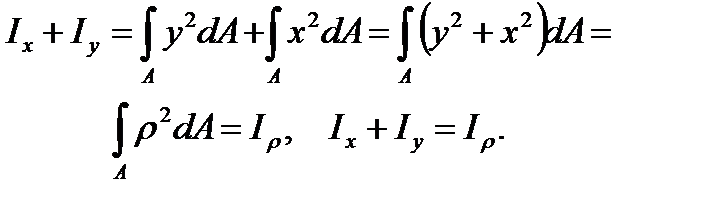(3.9)

As the sum integral is equal to the integrals sum, then we can determine the inertia moment of complicated figures as the sum of simple figures into which they can be divided. The concept of the axial moments of inertia will be necessary in studying the theory of bending. Determine the axial moments of inertia of some simple figures.

1. The rectangle with sides b and h (Fig. 3.3).

Select the infinite small area dA in the form of a stripe b with the height dy, then dA=bdy.

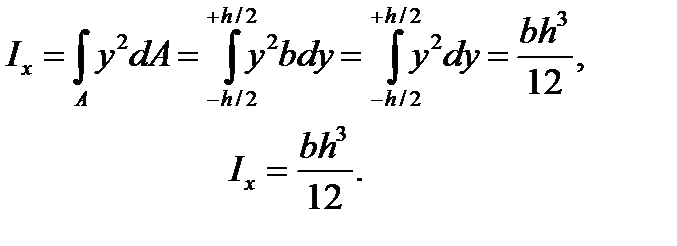(3.10)

For the square with the a side .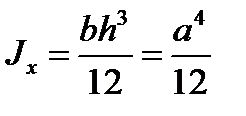

2. The circle with the b diameter about x and y axes. By symmetry we have 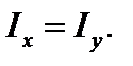As

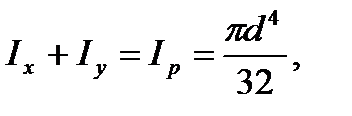
then

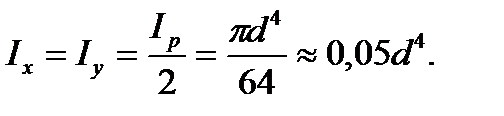(3.11)

3. The ring with dimensions of D х d about x and y axes:

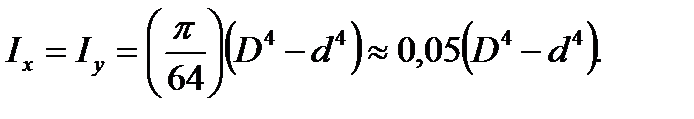(3.12)