Расчет двухрядной цилиндрической пружины

В качестве упругих элементов рессорного подвешивания вагонов в основном применяют винтовые цилиндрические пружины. Они позволяют получить необходимые упругие характеристики при небольших габаритах и массах. Пружины изготавливают в соответствии с требованиями ГОСТ 1452-69.

В эксплуатации пружины испытывают сложные переменные нагрузки. Поэтому, для точного определения целесообразных размеров пружины, необходимо иметь полную статическую характеристику нагрузок, которые испытывает пружина за все время эксплуатации. Если нет достаточного количества таких данных, выполняют приближенные расчеты, в которых косвенно учитывают факторы, влияющие на усталость рессор. Распространенным является расчет, при котором учитывается коэффициент конструктивного запаса прогиба.

При известной нагрузке на пружину необходимо сначала выбрать марку стали для изготовления пружины, чтобы принять допускаемые напряжения. Далее определить геометрические характеристики эквивалентной однорядной пружины и только потом перейти к расчету двухрядной.

Наибольший расчетный прогиб упругого элемента определяется по формуле[2]:

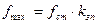, (7.1)

где 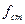- статический прогиб рессорного подвешивания, 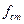= 0,05 мм;

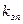- коэффициент конструктивного запаса прогиба, величина которого должна быть не менее для грузовых вагонов 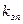=1,8;

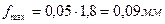
Наибольшую расчетную вертикальную силу определяют из выражения[1]:

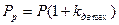, (7.2)

где 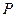- статическая нагрузка, действующая на двухрядную пружину, P = 29,63 кН;

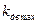- максимальное значение коэффициента вертикальной динамики, определяется по формуле[2]:

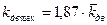(7.3)

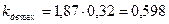
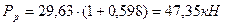
Диаметр прутка эквивалентной однорядной пружины определяется по формуле[2]:

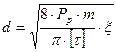, (7.4)

где 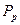- расчетная сила, 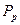= 47,35 кН;

m - индекс пружины, m = 5,5;

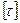- допускаемое касательное напряжение, 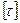= 750 МПа;

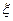- поправочный коэффициент, зависящий от индекса пружины, определяется по формуле[2]:

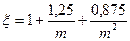
(7.5)

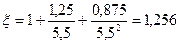
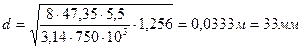
Средний диаметр эквивалентной пружины определяется по формуле[2]:

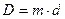(7.6)

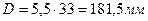
Число рабочих витков эквивалентной пружины определяется по формуле[2]:

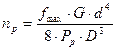, (7.7)

где G - модуль сдвига, G = 0,8*10¹¹ Па;

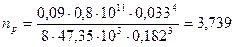
Высота пружины в сжатом состоянии определяется по формуле[2]:

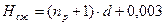(7.8)

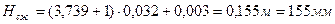
Высота пружины в свободном состоянии[2]:

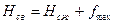(7.9)

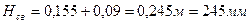
Диаметры прутков наружной и внутренней пружины определяется по формуле[2]:

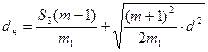, (7.10)

где d - диаметр прутка эквивалентной пружины, d = 30 мм;

- зазор между витками внутренней и наружной пружин, = 3 мм;

.

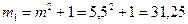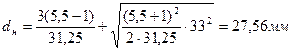
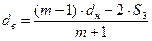
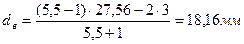
Средние диаметры наружной и внутренней пружин определяются по формулам[2]:

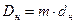(7.11)

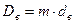
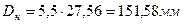
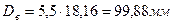
Число рабочих витков наружной и внутренней пружин определяются по формулам[2]:

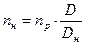(7.12)

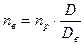(7.13)

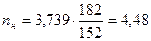
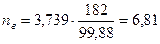
Высота пружин соответственно в сжатом и свободном состояниях[2]:

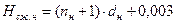(7.14)

(7.15)

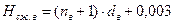
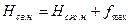( 7.16)

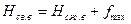(7.17)

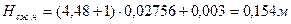
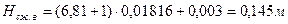
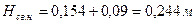
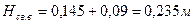
Жесткости наружной и внутренней пружин определяются по формулам[2]:

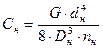
(7.18)

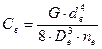(7.19)

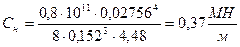
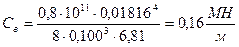
Жесткость комплекта определяется по формуле[2]:

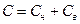(7.20)

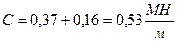
Нагрузки на наружную и внутреннюю пружины определяются из следующих выражений:

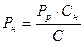
(7.21)

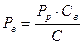(7.22)

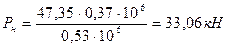
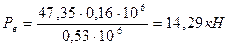
В качестве проверки правильности расчетов необходимо определить касательные напряжения для наружной и внутренней пружин, которые должны получиться равными допускаемому напряжению выбранной марки стали, по формулам[2]:

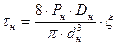
(7.23)

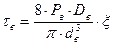(7.24)

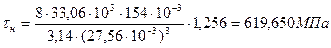
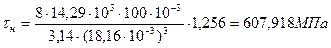
Полученные значения касательных напряжений необходимо сравнить с допускаемыми:

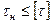
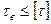
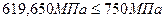
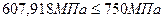
Поскольку условия выполняются, то можно говорить о том, что с данной осевой нагрузкой пружину с рассчитанными размерами применять можно.