Связь передаточных функций с моментами кривых

При использовании импульсного входного возмущения имеет место следующая связь:

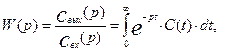(3.6.9)

так как с_вх(р)=1 для импульсного входа

Найдем значения производных разных порядков передаточной функции по оператору Лапласа:

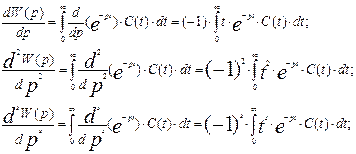(3.6.10)

Найдем теперь пределы правой и левой частей уравнения для производных при р®0. Заметим, что стремление к нулю оператора Лапласа соответствует стремлению к бесконечности реального времени t®¥.

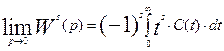(3.6.11)

Интеграл в правой части уравнения соответствует выражению начального момента порядка s для функции распределения.

Поэтому, окончательно получаем выражение для момента кривой распределения в следующем виде:

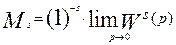, (3.6.12)

где s -порядок производной и начального момента.

Используя это уравнение можно найти связь между параметрами модели структуры потока и характеристиками экспериментально наблюдаемой кривой распределения – ее моментами, которые легко вычисляются с использованием методов численного расчета определенных интегралов.

Например, для модели идеального смешения, получим следующие выражения для производных передаточной функции:

Передаточная функция имеет вид:

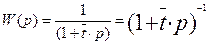(3.6.13)

Первая производная

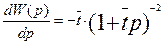(3.6.14)

Вторая производная

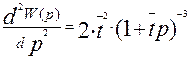(3.6.15)

Найдем моменты различного порядка как пределы производных при р®0:

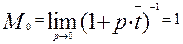(3.6.16)

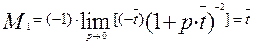(3.6.17)

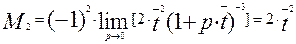(3.6.18)

Найдем центральные моменты кривой отклика аппарата идеального перемешивания:

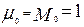; (3.6.19)

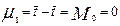; (3.6.20)

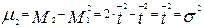(3.6.21)

Из полученных выражений видно, что первый начальный момент равен среднему времени пребывания в аппарате, а второй центральный момент равен дисперсии, причем .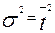

Для аппарата идеального вытеснения, с учетом значения передаточной функции, получаем следующие выражения:

;

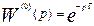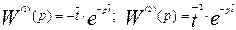(3.6.22)

Отсюда получаем следующие уравнения связи моментов с параметрами модели:

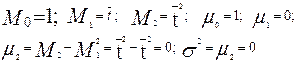(3.6.22)

Полученное выражение для m₂, показывает, что дисперсия s², т.е. рассеяние времени пребывания отдельных частиц в аппарате идеального вытеснения относительно среднего времени пребывания равно нулю. Таким образом, все частицы находятся в аппарате одно и то же время.

Ячеечная модель

Передаточная функция ячеечной модели имеет следующий вид:

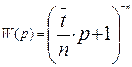(3.6.23)

После дифференцирования и нахождения пределов производных, можно найти следующие соотношения между моментами кривой распределения и параметрами модели:

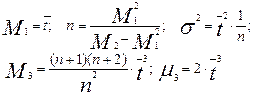(3.6.24)

Из выражения для дисперсии видно, что при n®¥ дисперсия s²®0. Это свидетельствует о том, что ячеечная модель при этом стремится к модели идеального вытеснения. Третий центральный момент является величиной положительной, следовательно функция распределения будет иметь правостороннюю асимметрию

(затянутый переходный процесс). На основании полученных формул для М₁ и М₂ обычно рассчитывают параметры модели ( и n) а третий момент используют для проверки адекватности модели.