Синхронизация приемника цифровой СПИ

Пример 21. При передаче цифрового телефонного сигнала в канале без помех в начале каждого байта дополнительно передается символ 1 в качестве синхросигнала. Чтобы установить синхронизацию, селектор синхросигналов из принятой последовательности выбирает наудачу каждый девятый символ и, набрав таким образом 15 битов, выносит решение о том, является ли синхросигналом выбранная подпоследовательность. Найти вероятность того, что будет принято верное решение, полагая, что информационные символы независимы и с одинаковой вероятностью принимают значения 0 и 1.

Решение. Селектор примет верное решение, если произойдет одно из двух несовместных событий:

1) выбранная наудачу подпоследовательность является синхросигналом и, следовательно, состоит из одних единиц; вероятность такого события Р₁ = 1/9;

2) выбранная подпоследовательность не является синхросигналом (вероятность такого события составляет 8/9) и не состоит из одних единиц.

Вероятность того, что 15 информационных символов состоят из одних единиц, находим по формуле умножения вероятностей независимых событий 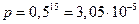. Следовательно, вероятность того, что они содержат хотя бы один ноль, равна (1–р) = 0,999969. Тогда вероятность события 2 равна

Р₂ = 0,999969·8/9 =0,888862.

В итоге вероятность того, что селектор примет верное решение, находим по формуле сложения вероятностей

Р = Р₁ + Р₂ = 0,111111 + 0,888862 = 0,999973.

Пример 22. Решить пример 21 при условии, что битовая вероятность независимых ошибок в симметричном канале равна р = 10^–3, а селектор выносит решение о наличии синхросигнала лишь в случае, когда количество единиц в выбранной подпоследовательности не менее 14.

Решение. Селектор примет верное решение, если произойдет одно из двух несовместных событий:

1) выбранная наудачу подпоследовательность является синхросигналом, а количество ошибок в ней не превышает единицы;

2) выбранная подпоследовательность не является синхросигналом и содержит менее 14 единиц.

Вероятность того, что в 15 принятых символах содержится не более одной ошибки, находим с использованием биномиальной формулы (3.57) [1]

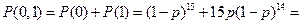
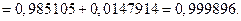
Вероятность события 1 равна Р₁ = 0,111111·0,999896 = 0,111100.

Если два передаваемых символа равновероятны, то они останутся равновероятными и на выходе симметричного канала с ошибками. Тогда вероятность того, что в 15 принятых информационных символах содержится более одного нуля, также находим с использованием биномиальной формулы, положив р = 0,5

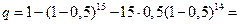
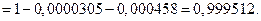
Вероятность события 2 равна Р₂ = 0,888889·0,999512 = 0,888455.

Селектор примет верное решение с вероятностью

Р = Р₁ + Р₂ = 0,111100 + 0,888455 = 0,999555.

Сети электросвязи

Пример 23. Девять компьютеров расположены в узлах квадратной решетки с шагом 5 м. Найти минимальную суммарную протяженность линий, если используется сеть топологии:

а) общая шина;

б) звезда;

в) полносвязная.

Решение. а) В сети топологии “общая шина” необходимо иметь 8 линий по 5 метров, то есть суммарная протяженность линий равна 40 метров.

б) В сети топологии “звезда” узел располагается в центре и необходимо иметь 4 линии по 5 метров и 4 линии по 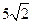метров, то есть суммарная протяженность линий равна 48,5 м.

в) В полносвязной сети имеется 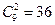линий. Их суммарная протяженность равна

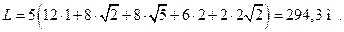
Пример 24. Определить общее количество линий в полносвязной сети, обслуживающей 1000 абонентов.

Решение. Число линий равно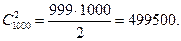

Пример 25. Локальная сеть имеет топологию “общая шина” и обслуживает 50 абонентов. Каждый абонент отправляет в среднем 100 пакетов в час через случайные интервалы времени, при этом средний размер пакета составляет 300 байтов. Пропускная способность общей шины составляет 100 Мбит/с. Найти вероятность того, что в случайно выбранный момент времени шина окажется свободной.

Решение. Абонент отправляет в час 100·300·8 = 240 кбит в среднем и занимает шину на 240/100000 = 0,0024 часа. Вероятность того, что в случайно выбранный момент времени он ее не занимает, равна 0,9976. Вероятность того, что ни один из 50 абонентов ее не занимает, находим по формуле умножения вероятностей Р = 0,9976⁵⁰ = 0,887.

Пример 26. АТС предприятия обслуживает М абонентов и имеет N-канальный выход на городскую телефонную сеть. Каждый абонент предприятия делает в среднем 1,2 исходящих звонка в час абонентам городской телефонной сети (входящие звонки исключены), при этом средняя продолжительность разговора составляет 2,7 минуты. Если не удается связаться с первой попытки, абонент звонит по сотовому телефону.

Рассматриваются два варианта:

а) М = 30, N = 2;

б) М = 90, N = 6.

Для обоих вариантов найти:

1) нагрузку, создаваемую одним абонентом;

2) общую нагрузку;

3) общее среднее количество требований на обслуживание в час;

4) среднюю интенсивность поступающих от абонента вызовов;

5) общую среднюю интенсивность вызовов, поступающих на АТС;

6) вероятность блокировки в системе;

7) среднюю величину нагрузки, приходящейся на один канал.

Решение. Нагрузка, создаваемая одним абонентом, измеряется в эрлангах. Она в обоих случаях одинакова и в соответствии с формулой (7.4) [2] равна

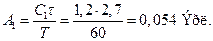
Одинакова и средняя интенсивность поступающих от абонента вызовов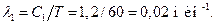

Общая нагрузка в обоих случаях разная. Она вычисляется по формуле (7.5) [2] и равна соответственно А_а = 1,62 Эрл и
А_б = 4,86 Эрл.

Общее среднее количество требований на обслуживание в час равно С_а = С₁М =1,2·30 = 36 час^–1 и С_б = 1,2·90 = 108 час^–1.

Общая средняя интенсивность вызовов, поступающих на АТС, равна соответственно λ_а = С_а/Т =0,6 мин^–1 и λ_б = 1,8 мин^–1.

Описанная система является системой с явными потерями, поэтому вероятность блокировки находим по формуле (7.10) [2], и тогда

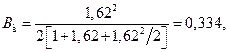
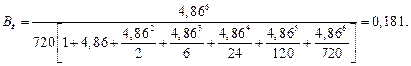Видно, что при увеличении размеров сети качество обслуживания улучшилось.

Нагрузку, приходящуюся на один канал, находим по формуле (7.11) [2]

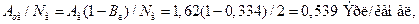
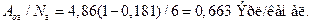
Во втором случае канал обслуживает большую часть поступающей нагрузки за счет того, что теряется меньше вызовов.

Пример 27. В условиях примера 26 полагаем, что абоненты, не обслуженные сразу, ставятся в очередь, причем длина очереди не ограничена.

Для обоих вариантов найти:

1) среднее время ожидания в очереди для абонентов, оказавшихся в ней;

2) вероятность того, что время ожидания в очереди не превысит 10 минут.

Решение. Среднее время ожидания в очереди находим по формуле (7.16) [2] 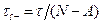и получаем

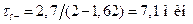в первом случае и

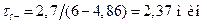во втором случае.

Вероятность того, что время ожидания в очереди t_оч не превысит t = 10 минут, находим по формуле (7.15) [2]

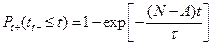и получаем

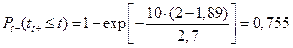в первом случае и 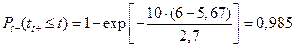во втором случае.