Математические модели сигналов

Пример 1. Случайная величина 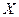– число бросаний монеты до первого выпадания герба. Найти:

а) ряд распределения случайной величины ,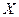

б) математическое ожидание ,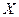

в) математическое ожидание двоичного логарифма вероятности .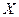

Решение. Возможные значения случайной величины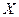

равны 1, 2, 3,... . Для осуществления события 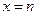необходимо, чтобы в первых 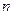-1 бросаниях выпадали решетки, а в n-м бросании выпал орел, поэтому 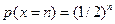по формуле умножения вероятностей независимых событии. Ряд распределения дан в табл. 1.

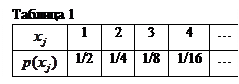Математическое ожи­дание числа броса­ний вычислим по форму­ле (1.2) [1], положив

,

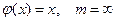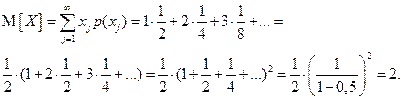
Математическое ожидание двоичного логарифма вероятности X также вычисляем по формуле (1.2) [1], положив 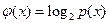, т. е.

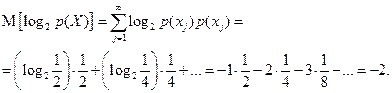
Пример 2. По двоичному каналу связи с помехами (рис. 1) передаются сообщения 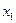и с априорными вероятностям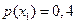и и 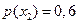. Влияние помех описывается переходными вероятностями:

, ,

, .

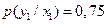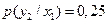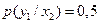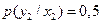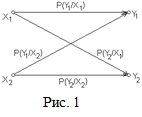Найти: а) безусловные вероятности сигналов на выходе канала;

б) наиболее вероятное значение 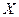, если ;

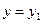в) наиболее вероятное значение 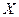, если .

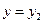Решение. Совместные вероятности сообщения 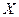и сигнала 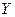вычисляем по формуле умножения вероятностей (1.8) [1]:

, ,

.

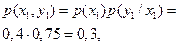
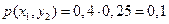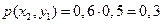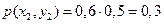Безусловные вероятности сигналов на выходе канала вычислим по формуле полной вероятности (1.7) [1]:

,

.

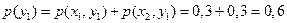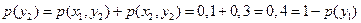Условные вероятности сообщений на входе находим по формуле Байеса (1.9) [1]:

,

,

,

.

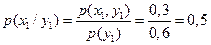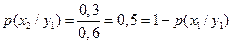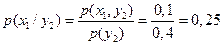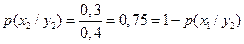Сравнив 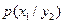и 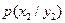, видим, что если принят сигнал 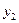, то более вероятно, что было передано сообщение . Сигнал 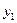мог быть с одинаковой вероятностью вызван сообщениям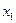и и .

Пример 3. Сигнал 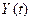на выходе непрерывного канала связи выражается через входной сигнал 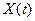соотношением 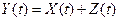, где 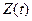– аддитивный нормальный стационарный белый шум с односторонней спектральной плотностью 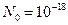В/Гц, ограниченный полосой от 0 до 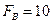МГц. Суммарная мощность составляющих в спектре сигнала 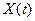, лежащих вне указанной полосы, пренебрежимо мала.

Осуществить квантование по времени сигнала 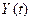на интервале от 0 до 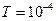секунды. Для конкретной реализации входного сигнала (в вольтах)

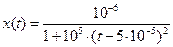
найти для квантованного сигнала:

а) вектор условных математических ожиданий;

б) условную корреляционную матрицу;

в) условную плотность вероятности квантованного сигнала на выходе.

Решение. Чтобы осуществить квантование непрерывного по времени сигнала 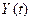, необходимо взять его отсчеты 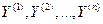в моменты времени 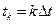, , 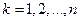где .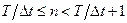

Верхняя граничная частота суммы сигнала с шумом равна 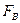, поэтому шаг квантования определяется в соответствии с теоремой Котельникова

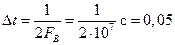мкс.

Требуемое число отсчетов равно .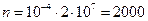

Каждый отсчет сигнала 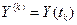является суммой двух величин

,

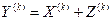где 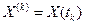- отсчет сообщения;

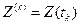- отсчет шума.

Вектор условных математических ожиданий сигнала состоит из следующих элементов

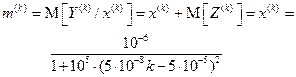
и определяется только передаваемым сообщением, так как математическое ожидание белого шума 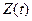равно нулю.

Условная корреляционная матрица B сигнала 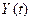при фиксированном 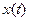состоит из следующих элементов

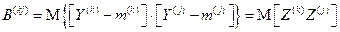
и равна корреляционной матрице отсчетов шума. Элементы этой матрицы есть отсчеты корреляционной функции шума

.

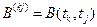Шум стационарен, поэтому его корреляционная функция зависит от разности аргументов 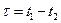и может быть найдена по теореме Винера – Хинчина (1.21) [1]

,

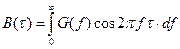где 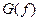– спектр плотности мощности шума.

По условию задачи, он равномерен в полосе 0… ,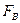

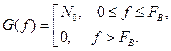
Находим выражение для корреляционной функции

.

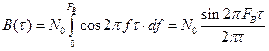Поскольку 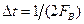, то

.

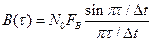Отсюда видно, что 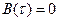при 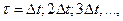т.е. отсчеты 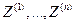, взятые с шагом квантования 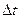, некоррелированы. Таким образом, в корреляционной матрице отсчетов сигнала не равны нулю будут только элементы, стоящие на главной диагонали,

,

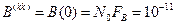численно равные дисперсии этих отсчетов (вольт²).

Условная плотность вероятности квантованного сигнала есть совместная плотность вероятности системы 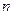некоррелированных (следовательно, и независимых) нормальных случайных величин

.

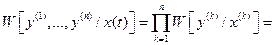
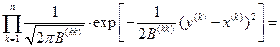
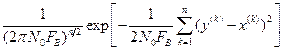Пример 4. Доказать, что для любой положительной случайной величины 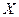(имеющей только положительные возможные значения) при 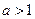справедливо неравенство Иенсена

.

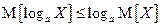Доказать, что для любой системы случайных величин 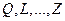и любой функции 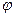, таких, что 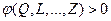при всех возможных значениях системы, справедливо аналогичное неравенство

.

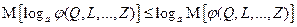Найти необходимые и достаточные условия, при которых неравенства обращаются в равенства.

Решение. Сначала убедимся, что непрерывная функция 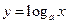является строго выпуклой вверх, т.е. ее вторая производная отрицательна при любых .

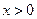Действительно,

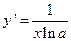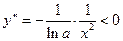, при .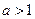

Следовательно, график функции 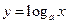лежит ниже касательной, проведенной в любой точке 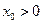(рис. 2):

,

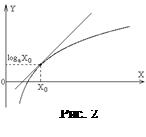
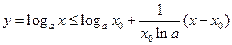причем знак равенства выполняется только в точке касания .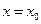

Предположим, что 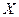– положительная случайная величина, тогда полученное неравенство справедливо для любого из ее возможных значений и, следовательно, при усреднении обеих частей знак неравенства сохранится:

.

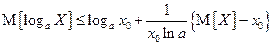Выбрав абсциссу точки касания 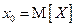, получим окончательно

.

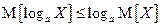Это неравенство обращается в равенство тогда и только тогда, когда все возможные значения случайной величины 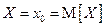, т.е. если величина X не случайна.

Пусть случайная величина 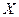получена в результате функционального преобразования системы случайных величин 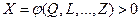, тогда в силу доказанного неравенства имеем

.

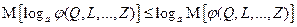Это неравенство обращается в равенство тогда и только тогда, когда величина 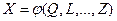не случайна.