Собственная информация. Взаимная информация
Пример 5. На экране индикатора РЛС, представляющего поле с 10 вертикальными и 10 горизонтальными полосами, появляется изображение объекта в виде яркостной отметки. Все положения объекта равновероятны.
Определить количество информации, содержащееся в сообщениях:
а) объект находится в 46-м квадрате экрана;
б) объект находится в 5-й горизонтальной строке экрана;
в) объект находится в 6-м вертикальном столбце и 3-й горизонтальной строке экрана.
Решение. а) Пусть  - сообщение о том, что объект находится в 46-м квадрате экрана.
- сообщение о том, что объект находится в 46-м квадрате экрана.
Собственная информация в этом сообщении по формуле (4.2) [1] равна 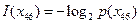 . Безусловная вероятность сообщения – объект находится в 46-квадрате экрана – равна
. Безусловная вероятность сообщения – объект находится в 46-квадрате экрана – равна  , где
, где 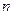 – общее число возможных исходов (квадратов поля),
– общее число возможных исходов (квадратов поля), 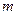 – число исходов, благоприятствующих событию
– число исходов, благоприятствующих событию  .
.
По условию задачи 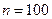 квадратов, a
квадратов, a 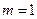 . Тогда
. Тогда
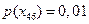 и
и 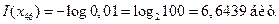
б) Вероятность события  – объект находится в 5-й горизонтальной строке экрана – по аналогии с рассмотренным случаем а) определится
– объект находится в 5-й горизонтальной строке экрана – по аналогии с рассмотренным случаем а) определится  и собственная информация
и собственная информация

в) Вероятность события 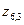 – объект находится в 6-м вертикальном столбце и 3-й горизонтальной строке – равна
– объект находится в 6-м вертикальном столбце и 3-й горизонтальной строке – равна
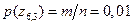 , следовательно,
, следовательно,
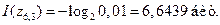
Пример 6. Рассматривается ансамбль сообщений, приведенный в табл. 2.
Таблица 2
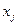
| 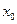
| 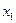
| 
| 
| 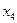
| 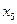
| 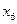
|
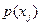
| 1/2 | 1/4 | 1/8 | 1/32 | 1/32 | 1/32 | 1/32 |
| Кодовое слово |
Сообщение 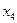 поступает в кодер. Вычислить дополнительную информацию об этом сообщении, доставляемую каждым последующим символом на выходе кодера.
поступает в кодер. Вычислить дополнительную информацию об этом сообщении, доставляемую каждым последующим символом на выходе кодера.
Решение. На вход кодера поступает одно из сообщений 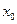 ,...,
,..., 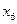 , а кодер порождает соответствующие таблице двоичные символы. Так, сообщению
, а кодер порождает соответствующие таблице двоичные символы. Так, сообщению 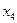 соответствует на выходе кодовое слово 101. Символы на выходе кодера появляются последовательно, т.е. первый символ 1, второй 0 и третий 1. Первый символ кодового слова содержит некоторую информацию относительно того, какое сообщение поступает на вход кодера. Так, первый символ 1 показывает, что на входе могли быть сообщения
соответствует на выходе кодовое слово 101. Символы на выходе кодера появляются последовательно, т.е. первый символ 1, второй 0 и третий 1. Первый символ кодового слова содержит некоторую информацию относительно того, какое сообщение поступает на вход кодера. Так, первый символ 1 показывает, что на входе могли быть сообщения  ,
, 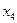 ,
, 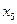 или
или 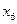 . Второй символ 0 сужает выбор – теперь на входе возможно одно из двух сообщений:
. Второй символ 0 сужает выбор – теперь на входе возможно одно из двух сообщений:  или
или 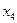 . И, наконец, последний, третий символ 1 однозначно определяет переданное сообщение.
. И, наконец, последний, третий символ 1 однозначно определяет переданное сообщение.
По формуле (4.19) [1] взаимная информация, содержащаяся в первом кодовом символе 1 относительно сообщения 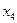 , равна
, равна
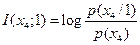 .
.
Обратная вероятность  может быть найдена по формуле Байеса (1.9) [1]
может быть найдена по формуле Байеса (1.9) [1]
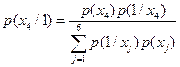 ,
,
где 
т.е. условная вероятность 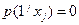 для гипотез, при которых первый кодовый символ есть 0, и
для гипотез, при которых первый кодовый символ есть 0, и  для гипотез, при которых первый кодовый символ 1. В знаменателе формулы Байеса таким образом учитываются те гипотезы, при которых возможно появление 1 на первом месте.
для гипотез, при которых первый кодовый символ 1. В знаменателе формулы Байеса таким образом учитываются те гипотезы, при которых возможно появление 1 на первом месте.
Итак,
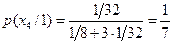 ,
,
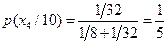 ,
,  ,
,
а взаимная информация, содержащаяся в первом кодовом символе 1 относительно сообщения 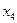 , равна
, равна

Информация, содержащаяся во втором кодовом символе 0 при условии, что первый кодовый символ был 1, есть
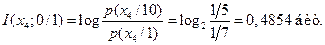
Информация, содержащаяся в третьем кодовом символе 1 при условии, что ему предшествовали 10, есть
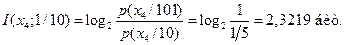
Так как сообщения 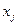 и кодовые слова однозначно связаны, то
и кодовые слова однозначно связаны, то
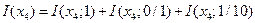 .
.
Действительно, 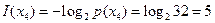 бит, и это совпадает с приведенной суммой.
бит, и это совпадает с приведенной суммой.
 Пример 7. По дискретному каналу передаются сообщения
Пример 7. По дискретному каналу передаются сообщения 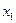 или
или  . Вследствие действия шумов на выходе появляется один из сигналов
. Вследствие действия шумов на выходе появляется один из сигналов 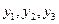 . Вероятности совместного появления
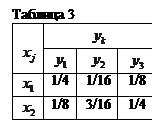
. Вероятности совместного появления 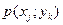 заданы табл. 3.
заданы табл. 3.
Вычислить взаимные информации  ,
, 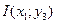 .
.
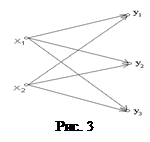
Решение. Дискретный канал с шумом удобно изображать в виде графа (рис. 3).
Определим взаимную информацию по формуле (4.19) [1]
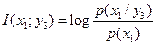
или в силу свойства симметрии
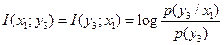 .
.
Условные и безусловные вероятности найдем, воспользовавшись таблицей. По формуле (1.7) [1]
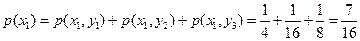 ;
;
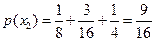 ;
; 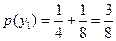 ;
;
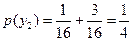 ;
; 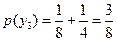 .
.
Используя формулы (1.9), (1.10) [1], найдем условные вероятности:
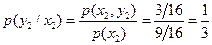 ,
,
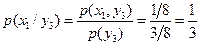 .
.
Тогда количество взаимной информации по формуле (4.19) [1]
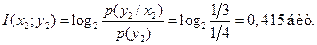

Мы получили 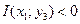 , так как
, так как 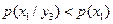 .
.
Пример 8. Производится стрельба по двум мишеням, по одной сделано 2 выстрела, по второй – 3. Вероятности попадания при одном выстреле соответственно равны 1/2 и 1/3. Исход стрельбы (число попаданий) по какой мишени является более определенным?
Решение. Исход стрельбы определяется числом попаданий в мишень, которое подчинено биномиальному закону распределения 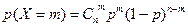 ,
,
 где
где 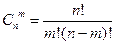 .
.
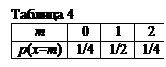
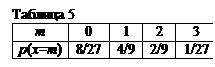 Составляем ряд распределения для числа попаданий в первую мишень при n=2 и p=1/2 (табл. 4) и вторую мишень при n=3 и p=1/3 (табл. 5).
Составляем ряд распределения для числа попаданий в первую мишень при n=2 и p=1/2 (табл. 4) и вторую мишень при n=3 и p=1/3 (табл. 5).
Мерой неопределенности исхода стрельбы служит энтропия числа попаданий. Энтропия числа попаданий при стрельбе по первой мишени (4.6) [1]
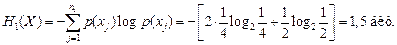
Аналогично для второй мишени имеем

т.е. исход стрельбы по второй мишени обладает большей неопределенностью.
Пример 9. Источник сообщений вырабатывает ансамбль символов
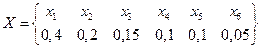 .
.
Символы в последовательности независимы.
Вычислить энтропию источника и определить избыточность.
Решение. Энтропия источника для случая неравновероятных и независимых сообщений определяется формулой (4.6) [1]

Избыточность за счет неоптимальности (неравновероятности) распределения сообщений в источнике определяется формулой (4.12) [1] 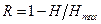 , где
, где 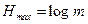 по формуле (2.2.3).
по формуле (2.2.3).
Отсюда 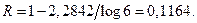
Пример 10. Алфавит источника состоит из трех букв:
х1, х2, х3.
Определить энтропию на 1 букву текста 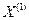 ,
, 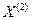 для следующих случаев:
для следующих случаев:
а) буквы алфавита неравновероятны: 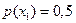 ,
, 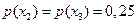 , а символы в последовательности на выходе источника статистически зависимы. Условные вероятности
, а символы в последовательности на выходе источника статистически зависимы. Условные вероятности 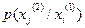 заданы в табл. 6;
заданы в табл. 6;
 б) вероятности букв те же, что и в п. а), но символы независимы;
б) вероятности букв те же, что и в п. а), но символы независимы;
в) символы в последовательности независимы, вероятности букв одинаковы.
Вычислить избыточность источников для случаев а) и б).
Решение. а) В случае неравновероятных и зависимых сообщений энтропия текста по формуле (4.10) [1]
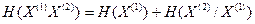 ,
,
где 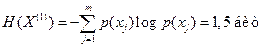 ,
,
а условная энтропия равна
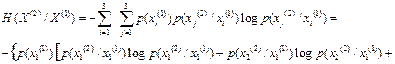
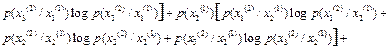

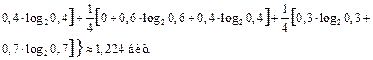
Энтропия на один символ
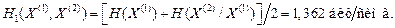
б) При неравновероятных, но зависимых сообщениях энтропия вычисляется по формуле (4.6) [1]
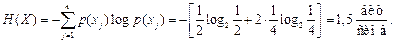
Избыточность, обусловленная статистической зависимостью
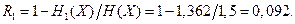
в) В случае равновероятных и независимых сообщений энтропия по формуле (4.7) [1]
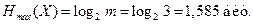
Избыточность, обусловленная неоптимальностью распределения вероятности

Полная избыточность (за счет неоптимальности распределения и наличия статистических взаимосвязей)
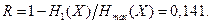
Пример 11. Вычислить для конкретного канала, заданного в примере 7, средние количества информации.
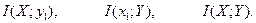
Решение. а) Средняя взаимная информация в реализации сигнала на выходе y1 относительно случайной величины X на входе канала определяется формулой
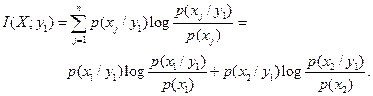
Из примера 7 известны вероятности:
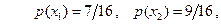

Определим условные вероятности:

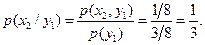
Средняя информация
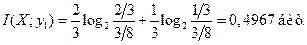
б) Средняя взаимная информация в выходной величине Y относительно реализации случайной величины на входе x1 определяется формулой
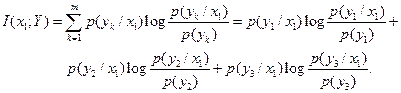
Определяем условные вероятности
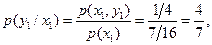
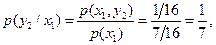
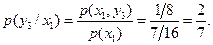
Условная средняя взаимная информация равна
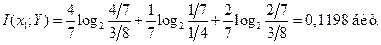
в) Средняя взаимная информация между случайной величиной Y на выходе канала и случайной величиной X на входе определяется формулой (4.23) [1]

Воспользовавшись результатами вычислений  , получим для средней взаимной информации
, получим для средней взаимной информации
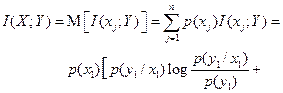
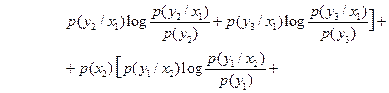
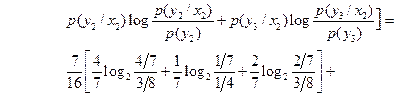
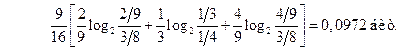
Пример 12. Эргодический источник имеет алфавит, состоящий из 8 букв. Средние частоты повторения букв одинаковы. При передаче по каналу с шумом в среднем половина всех букв принимается правильно, в другой половине случаев имеют место ошибки, при этом любая буква переходит в любую другую с одинаковой вероятностью. Какова средняя информация в принятой букве относительно переданной?
Решение. Обозначим
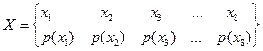 –
–
ансамбль переданных букв,
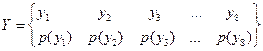 –
–
ансамбль принятых букв.
Так как для эргодической последовательности средние по времени частоты повторения букв совпадают с вероятностями, то по условию задачи вероятности появления букв на входе канала 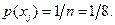
Ищем условные вероятности 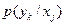 . Поскольку половина всех букв принимается правильно, то
. Поскольку половина всех букв принимается правильно, то 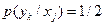 при
при 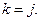
Другая половина случаев есть ошибочный прием, причем по условию задачи все возможные ошибки равновероятны. Числовозможных переходов (ошибок) равно 7. Тогда вероятность ошибки 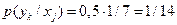 при
при 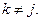

 Вероятности появления букв на выходе найдем по (1.7) [1]
Вероятности появления букв на выходе найдем по (1.7) [1]
 для любого к.
для любого к.
Этот же результат следует непосредственно из того факта, что рассматриваемый канал – симметричный (набор вероятностей ошибок одинаков для любого Х), тогда при равномерном распределении на входе распределение на выходе также равномерно.
Среднюю взаимную информацию находим по формуле (4.23) [1]
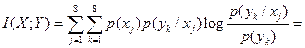
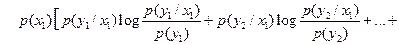
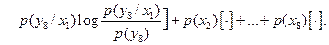
Выражения в квадратных скобках 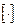 численно равны, поэтому
численно равны, поэтому

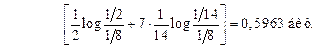
Пример 13. Сообщение X есть стационарная последовательность независимых символов, имеющих ряд распределения
 Сигнал Y является последовательностью двоичных символов, связанных с сообщением следующим неудачным образом: x1→00, x2→00, x3→1.
Сигнал Y является последовательностью двоичных символов, связанных с сообщением следующим неудачным образом: x1→00, x2→00, x3→1.
Определить: а) средние безусловную и условную энтропии, приходящиеся на 1 символ сообщения;
б) средние безусловную и условную энтропии, приходящиеся на 1 символ сигнала;
в) среднюю взаимную информацию в расчете на 1 символ сообщения.
Решение. Символы в последовательности на выходе источника независимы, поэтому из (4.30) [1]
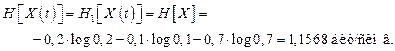
Обозначив y1=00, у2=1, вычислим условные и безусловные вероятности сигнала:
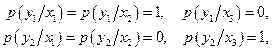
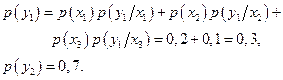
Энтропия случайной величины Y равна
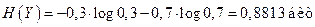 ,
,
а условная энтропия H(Y/X)=0, так как сигнал однозначно определяется сообщением.
Взаимная информация
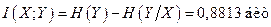 .
.
Условная энтропия сообщения
 .
.
Итак, получаем, что условная энтропия сообщения равна 0,2755 бит/симв, а взаимная информация в расчете на 1 символ сообщения равна 0,8813 бит/симв.
Среднее количество символов сигнала, приходящихся на 1 символ сообщения, равно
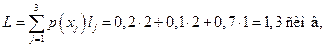
где lj – длина кодового слова, соответствующего xj.
Энтропия последовательности Y(t) равна

а условная энтропия равна нулю.
Пример 14. Вольтметром измеряется напряжение в электрической сети. Ошибка измерения не зависит от истинного значения напряжения и распределена нормально с нулевым математическим ожиданием и среднеквадратическим отклонением, равным 2 В. Истинное значение напряжения в сети также имеет нормальное распределение с математическим ожиданием 220 В и СКО, равным 10 В.
Найти:
а) зависимость величины получаемой информации от показаний прибора,
б) среднюю величину получаемой информации.
Решение. Введем обозначения:
X – напряжение в сети,
V – ошибка измерения,
Y = X + V – показание прибора.
Из условия задачи записываем плотности вероятностей:
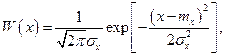
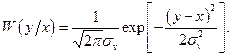
Безусловную плотность вероятности величины Y можно найти по формуле полной вероятности, но проще поступить следующим образом. Показание прибора Y есть сумма двух независимых нормальных случайных величия и, следовательно, Y также имеет нормальное распределение с математическим ожиданием

и дисперсией
 .
.
Итак,
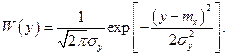
Условную плотность вероятности х находим по формуле Байеса
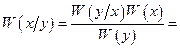
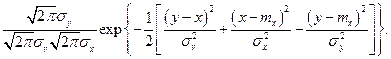
В выражении, стоящем под знаком экспоненты, осуществляем возведение в квадрат и затем группируем члены, содержащие х2 и х. В итоге убеждаемся, что условное распределение величины х также нормально
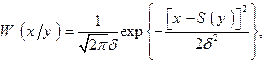
где 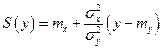 – условное математическое
– условное математическое
ожидание X,
 - условная дисперсия X.
- условная дисперсия X.
Для ответа на вопрос п. а) следует по формуле (3.1.2) вычислить величину средней взаимной информации между ансамблем X и реализацией у
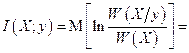
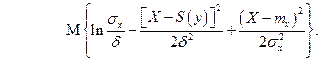
Находим квадраты разностей и выносим за знак математического ожидания слагаемые и множители, не зависящие от х. Далее учитываем, что вычисляются условные математические ожидания при конкретном значении у, поэтому
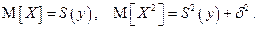
В итоге получаем

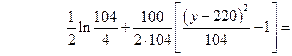
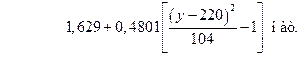
Таким образом, искомая зависимость есть параболическая функция разности 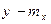 , причем наименьшее количество информации, равное 1,1482 нат, доставляет наиболее вероятное показание прибора
, причем наименьшее количество информации, равное 1,1482 нат, доставляет наиболее вероятное показание прибора 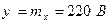 .
.
Для ответа на вопрос п. б) необходимо найти среднюю величину взаимной информации между ансамблями X и Y. Вычисляем безусловное математическое ожидание величины I(Х; у). При этом учитываем, что 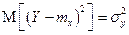 , и получаем
, и получаем

Обратите внимание, что в среднем количество получаемой информации в данном примере зависит только от отношения «сигнал/ошибка» 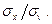
Пример 15. Положительная непрерывная случайная величина X распределена по экспоненциальному закону с математическим ожиданием mх=3. Вычислить значение дифференциальной энтропии величины X.
Решение. Заданный закон распределения имеет вид
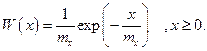
Дифференциальная энтропия непрерывной случайной величины X определяется формулой (4.40) [1]
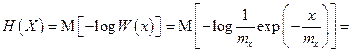

Подставляя mx = 3, получим
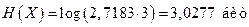 .
.
Кодирование
 Пример 16. Закодировать сообщения источника, приведенные в табл 7, двоичным кодом Хафмана. Оценить эффективность полученного кода.
Пример 16. Закодировать сообщения источника, приведенные в табл 7, двоичным кодом Хафмана. Оценить эффективность полученного кода.
Решение. В соответствии с алгоритмом построения кода Хафмана делаем последовательно следующие шаги:
1) располагаем сообщения источника в порядке убывания вероятностей;
2) образуем вспомогательный алфавит, объединяя наиболее маловероятные буквы u1 и u4 (m0=2), тогда вероятность новой буквы равна p1=р(u1)+р(u4)=0,1+0,05=0,15. Оставляем эту букву на месте, так как p1=р(u6);
3) объединяем первую вспомогательную букву и букву u6, тогда вероятность второй вспомогательной буквы равна р2=р1+р(u6)=0,15+0,15=0,3; перемещаем ее вверх в соответствии с этой вероятностью;
4) объединение продолжаем до тех пор, пока в ансамбле не останется единственное сообщение с вероятностью единица.
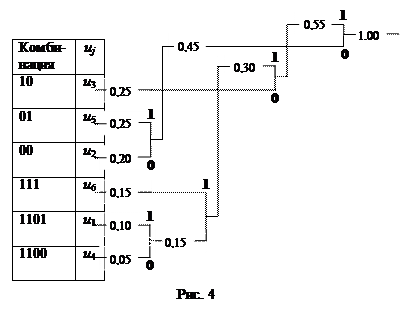 Построение кода Хафмана приведено на рис. 4.
Построение кода Хафмана приведено на рис. 4.
Сообщения источника являются теперь концевыми узлами кодового дерева. Приписав концевым узлам значения символов 1 и 0, записываем кодовые обозначения, пользуясь следующим правилом: чтобы получить кодовое слово, соответствующее сообщению u4, проследим переход u4 в группировку с наибольшей вероятностью, кодовые символы записываем справа налево (от младшего разряда к старшему), получим 1100.
Для сообщения u1 – 1101 и т.д. (см. рис. 4).
Оценим эффективность полученного кода.
Энтропия источника сообщений:

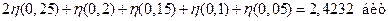
на одну букву на выходе источника.
Средняя длина кодового слова (формула (4.14) [1])
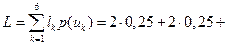
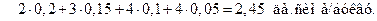 .
.
Для оценки эффективности кода используем коэффициент эффективности 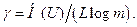
Для оптимального двоичного кода 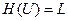 и
и 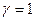 .
.
Полученный нами код имеет 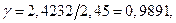 избыточность R=0,0109, т.е. код близок к оптимальному.
избыточность R=0,0109, т.е. код близок к оптимальному.
Пример 17. Сообщение источника X составляется из статистически независимых букв, извлекаемых из алфавита А, В, С с вероятностями 0,7; 0,2; 0,1. Произвести двоичное кодирование по методу Шеннона-Фано отдельных букв и двухбуквенных блоков. Сравнить коды по их эффективности.
Решение.Производим побуквенное кодирование методом Шеннона-Фано.
1) Располагаем буквы алфавита источника в порядке убывания вероятностей.
2) Делим алфавит источника на две (m=2) примерно равновероятные группы. Всем сообщениям верхней группы (буква А) приписываем в качестве первого кодового символа 1, всем сообщениям нижней группы приписываем символ 0.
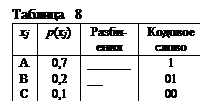 3) Производим второе разбиение на две группы (буквы В и С) и снова букве в верхней группе (В) приписываем символ 1, а в нижней (С) в качестве второго символа кодового слова приписываем 0. Так как в каждой группе оказалось по одной букве, кодирование заканчиваем. Результат приведен в табл. 8.
3) Производим второе разбиение на две группы (буквы В и С) и снова букве в верхней группе (В) приписываем символ 1, а в нижней (С) в качестве второго символа кодового слова приписываем 0. Так как в каждой группе оказалось по одной букве, кодирование заканчиваем. Результат приведен в табл. 8.
Оценим эффективность полученного кода. Энтропия источника
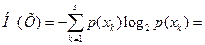
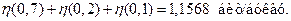
Средняя длина кодового слова
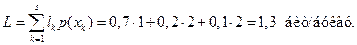 .
.
Видим, что L>H(X), и коэффициент эффективности
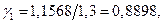 а избыточность R1=0,1102.
а избыточность R1=0,1102.
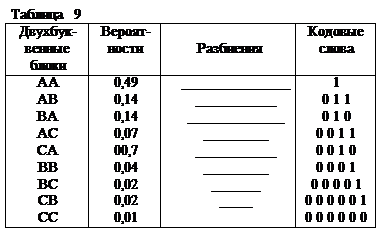 Покажем, что кодирование блоками по 2 буквы (k=2) увеличивает эффективность кода. Строим вспомогательный алфавит из N=32 блоков. Вероятности блоков находим по формуле (1.8) [1], считая буквы исходного алфавита независимыми. Располагаем блоки в порядке убывания вероятностей и осуществляем кодирование методом Шеннона-Фано. Все полученные двухбуквенные блоки, вероятности их и соответствующие кодовые обозначения сведены в табл. 9.
Покажем, что кодирование блоками по 2 буквы (k=2) увеличивает эффективность кода. Строим вспомогательный алфавит из N=32 блоков. Вероятности блоков находим по формуле (1.8) [1], считая буквы исходного алфавита независимыми. Располагаем блоки в порядке убывания вероятностей и осуществляем кодирование методом Шеннона-Фано. Все полученные двухбуквенные блоки, вероятности их и соответствующие кодовые обозначения сведены в табл. 9.
При блоковом кодировании средняя длина кодового слова на одну букву
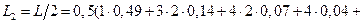
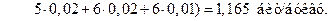 .
.
При этом коэффициент эффективности
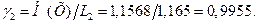
Избыточность при двухбуквенном кодировании R2=0,0045.
Получили γ2 > γ1, R2<<R1, что и требовалось показать.
Пример 18. Способ кодирования задан кодовой таблицей
 a) составить матрицу расстояний
a) составить матрицу расстояний 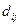
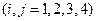 ;
;
б) найти кодовое расстояние;
в) определить кратности обнаруживаемых и исправляемых ошибок;
г) определить избыточность кода, полагая буквы источника равновероятными.
Решение. а) Матрицу расстояний записываем в виде таблицы (табл. 10).
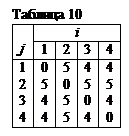 б) По табл. 10 находим кодовое расстояние
б) По табл. 10 находим кодовое расстояние 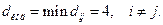
в) Кратность обнаруживаемых ошибок определяется по формуле (3.5) [1], откуда qо≤3.
Кратность исправляемых ошибок находим по формуле (3.6) [1] qи≤1,5.
Следовательно, приведенный код позволяет обнаруживать всевозможные однократные, двукратные и трехкратные ошибки и исправлять любые однократные ошибки.
г) Избыточность кода находим из следующих соображений. Для передачи равновероятных сигналов a1,а2, а3, а4 достаточно передавать кодовые слова 00, 10, 01 и 11 соответственно. Такой код не имеет избыточности, но не позволяет обнаруживать и, тем более, исправлять ошибки. Для обнаружения и исправления ошибок введены пять избыточных символов, т.е. количественно избыточность равна 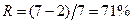 .
.
Пример 19. Линейный блочный (5,2)-код задан производящей матрицей G в систематической (канонической) форме
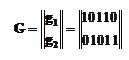 Пусть принят вектор b=00110 и известно, что возможны только одиночные ошибки.
Пусть принят вектор b=00110 и известно, что возможны только одиночные ошибки.
Произвести декодирование следующими методами:
а) по минимуму расстояния;
б) вычислением синдрома.
Решение. Если производящая матрица записана в каноническом виде, это значит, что она состоит из двух блоков: диагональной матрицы размера k 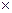 k, состоящей из единиц, и прямоугольной матрицы размера r
k, состоящей из единиц, и прямоугольной матрицы размера r 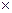 k. В этом случае первые k символов в любом кодовом слове являются информационными.
k. В этом случае первые k символов в любом кодовом слове являются информационными.
Проверочная матрица Н также может быть записана в каноническом виде и состоит из двух блоков. Первый блок есть прямоугольная матрица размера k 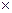 r, полученная транспонированием второго блока матрицы G. В качестве второго блока матрицы Н записывают диагональную матрицу размера r
r, полученная транспонированием второго блока матрицы G. В качестве второго блока матрицы Н записывают диагональную матрицу размера r 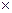 r, состоящую из единиц.
r, состоящую из единиц.
Для заданного кода получаем
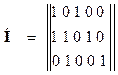 .
.
Убедимся, что полученная таким образом матрица Н удовлетворяет соотношению (3.18) [1]. Действительно,
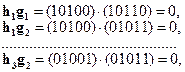
т.е. все 6 элементов матрицы GHT равны нулю.
Построим кодовую таблицу, воспользовавшись правилом образования кодовых слов по формуле (3.21) [1]:
a1=00000, а2=10110, а3=01011, а4=11101=a2+a3.
Всего кодовая таблица содержит 2k = 4 вектора.
Из кодовой таблицы определяем величину кодового расстояния 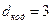 .
.
Следовательно, рассматриваемый код обнаруживает однократные и двукратные ошибки и исправляет однократные.
Декодируем принятый вектор b = 00110.
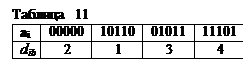 а) Метод декодирования по минимуму расстояния заключается в том, что, вычислив расстояния вектора b относительно всех векторов аi кодовой таблицы, отождествляем принятый вектор с тем, расстояние до которого минимально. Расстояния dib приведены в табл. 11.
а) Метод декодирования по минимуму расстояния заключается в том, что, вычислив расстояния вектора b относительно всех векторов аi кодовой таблицы, отождествляем принятый вектор с тем, расстояние до которого минимально. Расстояния dib приведены в табл. 11.
По величине dib min=1 решаем, что передавался вектор а2=10110, следовательно, ошибка в первом символе кодового слова, а информационная последовательность имеет вид х = 10.
б) Метод декодирования с помощью вычисления синдрома включает следующие операции:
1) По формуле (3.17) [1] заранее устанавливаем однозначную связь между векторами однократных ошибок е и соответствующими им синдромами. Все возможные векторы  приведены в табл. 12.
приведены в табл. 12.
 2) Вычисляем синдром для принятого слова b по формуле (3.16) [1] с=bHT:
2) Вычисляем синдром для принятого слова b по формуле (3.16) [1] с=bHT:
c1=(00110)(10100)=1, с2=(00110)(11010)=1,
с3=(00110)(01001)=0,
т.е. вектор с = 110. Синдром не равен нулю, следовательно, есть ошибка.
Вектору с = 110 в табл. 12 соответствует вектор ошибки в первом символе е=10000. Декодируем, суммируя принятый вектор с вектором ошибки 
Итак, получили тот же результат: передавался вектор a2=10110, соответствующий информационной последовательности х=10.
Пример 20. Для кода, заданного в примере 19, составить схему кодирующего устройства.
Решение. Обозначим буквами а1,...,а5 символы на выходе кодера, причем а1 и а2 есть информационные символы, поступающие на его вход, а символы а3, а4 и а5 образуются в кодере.
Из соотношения (3.22) [1] получаем
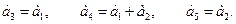
Один из вариантов схемы кодера, определяемой этими соотношениями, показан на рис. 5.
Кодирующее устройство работает следующим образом. В течение первых двух шагов двухразрядный регистр сдвига заполняется информационными символами а1 и а2, а в течение  следующих трех тактов его состояние сохраняется неизменным. Одновременно с заполнением регистра начинается переключение мультиплексора (переключателя) MUX. Таким образом формируются 5 символов кодового слова, удовлетворяющих требуемым соотношениям.
следующих трех тактов его состояние сохраняется неизменным. Одновременно с заполнением регистра начинается переключение мультиплексора (переключателя) MUX. Таким образом формируются 5 символов кодового слова, удовлетворяющих требуемым соотношениям.
Пример 21. Построить код Хэмминга, имеющий параметры: dкод=3, r=3.
Решение. Построение кода начинаем с проверочной матрицы. В качестве семи столбцов проверочной матрицы Н выбираем всевозможные 3-разрядные двоичные числа, исключая число нуль. Проверочная матрица имеет вид
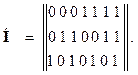
Чтобы определить места проверочных и информационных символов, матрицу Н представляем в каноническом виде
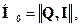 где I – единичная матрица.
где I – единичная матрица.
Для этого достаточно в матрице Н выбрать столбцы, содержащие по одной единице, и перенести их в правую часть. Тогда получим
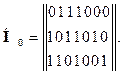
Из формулы (4.3.5) получаем следующие соотношения для символов a1, ..., а7 кодового слова:
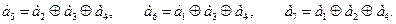
Пользуясь этими соотношениями, составляем кодовую таблицу
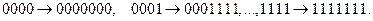
Пример 22. Для кода Хэмминга, определяемого проверочной матрицей H, построенного в примере 21, декодировать принятый вектор 1011001.
Решение. Для принятого вектора b=1011001 по формуле (3.16) [1] вычисляем синдром

Синдром с≠0, т.е. имеет место ошибка. В случае одиночной ошибки (и только лишь) вычисленное значение синдрома всегда совпадает с одним из столбцов матрицы Н, причем номер столбца указывает номер искаженного символа. Видим, что ошибка произошла в первом символе и передавался вектор 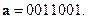
Пример 23. Производится кодирование линейным блочным кодом (15,15-r). Найти минимальное количество проверочных символов r, при котором код был бы способен исправлять любые однократные, двукратные и трехкратные ошибки.
Решение.Поскольку в кодовой комбинации n=15 символов, то количество всевозможных однократных ошибок (q=1) равно 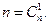 Количество различных двукратных и трехкратных ошибок равно числу сочетаний
Количество различных двукратных и трехкратных ошибок равно числу сочетаний 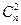 и
и 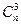 соответственно. Тогда суммарное количество всевозможных ошибок при q≤3 равно
соответственно. Тогда суммарное количество всевозможных ошибок при q≤3 равно

Чтобы любая из этих ошибок могла быть исправлена, нужно, чтобы разным ошибкам соответствовали различные значения синдрома c. Вектор c состоит из r двоичных символов, тогда максимальное количество различных ненулевых комбинаций равно 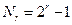 (нулевая комбинация c=0 соответствует отсутствию ошибок). Отсюда получаем
(нулевая комбинация c=0 соответствует отсутствию ошибок). Отсюда получаем 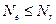 (это ограничение называется пределом Хэмминга), то есть
(это ограничение называется пределом Хэмминга), то есть
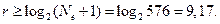
Таким образом, для исправления всех упомянутых ошибок необходимо, чтобы передаваемые комбинации содержали не менее 10 проверочных символов, т.е. k=5.
Пример 24. Для кодирования применяется (15,5)-код БЧХ с кодовым расстоянием dкод=7, способный исправить все ошибки до трехкратных включительно.
Битовая вероятность ошибки в канале передачи p=10-4, ошибки независимы. Определить вероятность ошибки при декодировании кодовой комбинации и битовую вероятность ошибки на выходе декодера.
Решение.Вероятность ошибки при декодировании кодовой комбинации определим по формуле (3.59) [1]
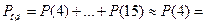
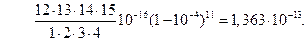
Битовую вероятность ошибки на выходе декодера определим по формуле (3.60) [1]  то есть, одна ошибка приходится в среднем на
то есть, одна ошибка приходится в среднем на 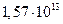 бит.
бит.
Дата добавления: 2020-10-25; просмотров: 646;










