Принцип регулирования по задающему воздействию

Этот принцип применяется в системах программного регулирования и следящих системах, когда действие возмущения минимально (так как возмущения должны быть минимальны, то для систем стабилизации не применяется).

Изобразим структурную схему следящей системы (например).

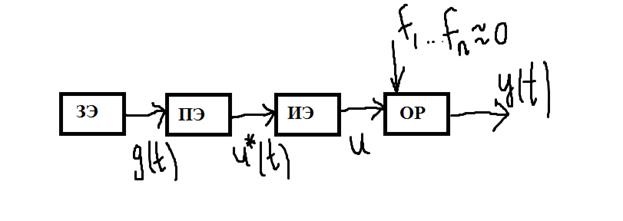
ЗЭ – задающий элемент.

ПЭ – преобразовательный элемент.

ИЭ – исполнительный элемент.

ОР – объект регулирования.

Если сравнить с обобщённой структурной схемой САР, то тут отсутствуют: датчик управляемой переменной, датчики возмущения и регулирующее устройство (тут фактически регулирующим устройством является ПЭ).

Управляющее воздействие u формируется на основе задающего воздействия. Информации о возмущении и текущем состоянии нету.

Обычно, когда проектируют, исходят из того, что входной сигнал гармонический:

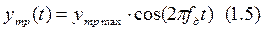
Основным показателем качества служит гармоническая ошибка.

Возникает вопрос – а какой сигнал g(t) надо формировать на выходе задающего элемента?

Воспользуемся самыми простыми математическими моделями:

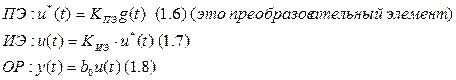
Найдём математическую модель всей системы. Это значит, y(t) надо связать с g(t): y(t) = f(g[t]).

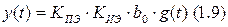
На практике широко используются математические модели, которые называют структурными моделями и в которых математические операции изображаются в виде схемы (для каждой математической операции своё условное обозначение). Например, для операции умножения используют прямоугольник, на входе указывается первый множитель, а внутри выставляется то, на что надо умножить. К_ПЭ – параметр преобразовательного элемента. Далее рисунок – графическое изображение (три прямоугольника etc). Эта схема называется структурной моделью следящей системы. Она раскрывает математическую структуру системы. В ней заложены три формулы (1.6 – 1.8). 1.9 – математическая модель всей системы.

К этой системе предъявляются требования: y_{у max} = y_{тр max}.

В формулу 1.9 подставим 1.5.

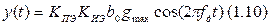
g(t) и y(t) могут иметь разные физические смыслы. g(t) – цифровой код, а y(t) может, например, являться сигналом для поворота зеркала в сканере. Требования ещё: f_y = f_g = const.

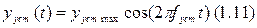
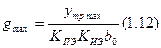
В световом сканере исполнительным элементом является шаговый двигатель, на который поступает код с указанием угла, на который надо повернуть. Никаких датчиков не применяют, так как не нужна цуперточность. Но теоретически это всё замечательно. Главное – подобрать, чтобы задающий элемент выдавал точность. Все погрешности связаны только с неточностью задания g(t).

Теперь зададимся другой моделью объекта регулирования (а все остальные элементы сохраним):

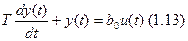
Теперь требование: надо, чтобы амплитуда была опять равна требуемой амплитуде. Но теперь новый объект, и нужна теперь другая модель.

Как только в какой-то математической модели появляется производная, то в этом случае коэффициент передачи на разной частоте имеет разное значение. Поэтому

АЧХ – это зависимость коэффициента передачи от частоты в установившемся режиме, когда на входе и на выходе действуют гармонические колебания либо постоянный сигнал (нулевая частота).

Предыдущая модель была справедлива и для переходного режима, и для установившегося, потому что никаких инерционностей не было.

1.13 – было похожее в ОТЦ. RC-цепочка, выходной сигнал – напряжение на обкладках конденсатора, а входным сигналом – напряжение на входе цепочки. В этом случае будет иметь место переходной процесс, его время t_п приблизительно равно (3-5)Т (постоянных времени).

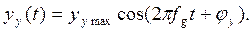
φ_у – это фазовый сдвиг между колебаниями на выходе и между колебаниями на входе.

Предъявим требование: надо подобрать такое g(t), чтобы на частоте f_g точно устанавливалась амплитуда, равная требуемой. При этом фазовый сдвиг не играет никакой роли (это проще).

Надо разработать структурную модель этой системы для установившегося режима. Она должна связывать амплитуду регулируемой величины y(t) с амплитудой задающего воздействия. Строим структурную модель:

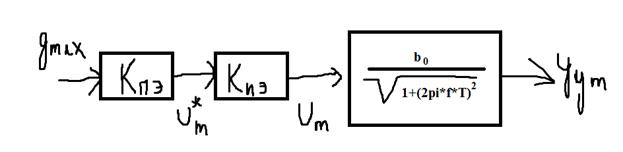
А_ОР – коэффициент передачи объекта регулирования на произвольной частоте.

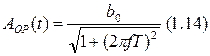
Т – постоянная времени объекта регулирования.

Надо, чтобы при f = f_g y_{y max} = y_{тр max}.

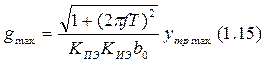
Достоинства системы:

1) Простота.

2) Дешевизна системы.

3) Отсутствие расходящихся процессов.

Недостатки:

1) Если возмущения будут значительными, то этот принцип будет неприменим.

У первого объекта b₀ – это коэффициент передачи. А для второго b₀ – это коэффициент передачи на нулевой частоте (равной нулю).