Построение сетевых графиков, согласно заданному порядку предшествования работ.
Пример 1. Задан следующий порядок предшествования работ:
 A, B, C << D;
A, B, C << D;
A, B << E;
A << F;
D, E << G;
F, G << H.
Решение приведено на рис.2.4.7.

Рисунок 2.4.7. Фрагмент сетевого графика
Пример 2.Начертить фрагмент сетевого графика, удовлетворяющего следующим условиям:
А, В, С << D;
A, C << E;
A, B <<G;
B, E << H.
Решение приведено на рис.2.4.8.

 В
В
 |  |  |

 H
H




 D G
D G


 A
A


 C
C
 E
E
Рисунок 2.4.8. Фрагмент сетевого графика
2. Расчет временных параметров сетевой модели и приведение критического времени к заданному сроку.
Пример 3. Исходный сетевой график приведен на рис 2.4.9.
Рассчитаем временные параметры сетевого графика.
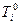 – ранние сроки свершения события;
– ранние сроки свершения события;
 – поздний срок свершения события;
– поздний срок свершения события;
Найдем критический путь – это максимально длинная по времени цепочка, соединяющая первое и последнее событие, которое определяет минимальное время выполнения всего проекта.
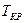 – критическое время. Результаты расчетов приведены на рис 2.4.9.
– критическое время. Результаты расчетов приведены на рис 2.4.9.
Необходимо привести 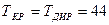 . Приводить будем за счет уменьшения времени работ критического пути. Результаты расчетов приведены на рис 2.4.10.
. Приводить будем за счет уменьшения времени работ критического пути. Результаты расчетов приведены на рис 2.4.10.
Составим таблицу временных характеристик приведенного сетевого графика выполнения работ. Где:
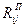 – полный резерв работ;
– полный резерв работ;
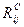 – свободный резерв работ.
– свободный резерв работ.
Свободный и полный резервы работ рассчитываются по формулам 2.4.5 и 2.4.6.
Результаты расчетов приведены в табл. 2.4.3.
На рисунке 2.4.11 показана линейная диаграмма, построенная по раннему сроку свершения событий.

Таблица 2.4.3
Таблица временных характеристик работ
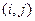
| 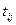
| 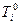
| 
| 
|
| (1,2) | ||||
| (1,3) | ||||
| (2,4) | ||||
| (3,6) | ||||
| (3,5) | ||||
| (4,7) | ||||
| (5,6) | ||||
| (5,8) | ||||
| (5,9) | ||||
| (9,13) | ||||
| (6,7) | ||||
| (6,10) | ||||
| (6,8) | ||||
| (8,12) | ||||
| (8,13) | ||||
| (7,11) | ||||
| (10,12) | ||||
| (11,14) | ||||
| (12,14) | ||||
| (12,15) | ||||
| (13,15) | ||||
| (14,15) |
Рисунок 2.4.11
 Линейная диаграмма раннего срока свершения событий
Линейная диаграмма раннего срока свершения событий
Пример 4. Задан сетевой график (Рисунок 2.4.12).
22 10 12

12 18 12 5 18
8 8 5
17 10
10 6 8
Рисунок 2.4.12 – Схема проведения работ
Необходимо выполнить расчет временных параметров. Привести Ткр к Тдир. (Тдир =72 дня).
Решение:
1) Рассчитываем временные характеристики событий (см. рисунок 2.4.13)



 2 13 14
2 13 14

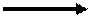
 12 12 42 10 42 52 52 64 64
12 12 42 10 42 52 52 64 64



 0 0 0 0
0 0 0 0
 8 11
8 11
40 41 45 72

 1 27
1 27




 1
1
0 0 5 7 12 15
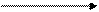 0 30 30 38 69 50 77 82 82
0 30 30 38 69 50 77 82 82
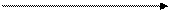 0 31 27 0
0 31 27 0
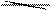



3 4 6 9
 17 46 27 56 33 62 41 70
17 46 27 56 33 62 41 70
29 29 29 29
Рисунок 2.4.13 – расчет сетевого графика
2) Заносим в таблицу 2.4.4 необходимые параметры сетевого графика Таблица 2.4.4 – Параметры сетевого графика
| i,j | ti,j | Т0i | Riпj | Riсj |
| 1,2 | ||||
| 1,3 | ||||
| 2,5 | ||||
| 2,10 | ||||
| 3,4 | ||||
| 3,7 | ||||
| 4,6 | ||||
| 5,7 | ||||
| 5,8 | ||||
| 5,10 | ||||
| 6,9 | ||||
| 7,12 | ||||
| 8,11 | ||||
| 8,13 | ||||
| 9,15 | ||||
| 10,13 | ||||
| 11,12 | ||||
| 12,15 | ||||
| 13,14 | ||||
| 14,15 |
3) Приводим Ткр к Тдир. (Тдир =72 дня). Для этого сократим время исполнения работ (13,14) и (14,15) на 4 и 6 дней соответственно за счет привлечения дополнительных ресурсов.
Тогда сетевой график будет выглядеть, как изображено на рисунке 2.4.14. А параметры откорректированного графика приведены в таблице 2.4.5.
Таблица 2.4.5 – Параметры откорректированного сетевого графика
| i,j | ti,j | Т0i | Riпj | Riсj |
| 1,2 | ||||
| 1,3 | ||||
| 2,5 | ||||
| 2,10 | ||||
| 3,4 | ||||
| 3,7 | ||||
| 4,6 | ||||
| 5,7 | ||||
| 5,8 | ||||
| 5,10 | ||||
| 6,9 | ||||
| 7,12 | ||||
| 8,11 | ||||
| 8,13 | ||||
| 9,15 | ||||
| 10,13 | ||||
| 11,12 | ||||
| 12,15 | ||||
| 13,14 | ||||
| 14,15 |

2 10 13 14
12 12 42 42 52 52 60 60
0 0 0 0
8 11
40 41 45 62
1 17
0 0 5 7 12 15
0 30 30 38 59 50 67 72 72
0 21 17 0
3 4 6 9
17 36 27 46 33 52 41 60
19 19 19 19
Рисунок 2.4.14 – Корректированный сетевой график
3. Построение сетевых графиков, согласно заданному порядку предшествования работ, расчет временных параметров сетевой модели и формирование планов ранних и поздних сроков.
Пример 5. Построить сетевую модель и календарный график потребления ресурсов в ранние и поздние сроки по указанным в таблице 2.4.6 данным.
Таблици 2.4.6
| Номера работ | Каким работам предшествует | Продолжитель-ность работ | Потребность в трудресурсах |
| 3, 4, 5 | |||
| 10, 12 | |||
| 9, 10 | |||
| 10, 12 | |||
| 13, 17 | |||
Решение:
На основе данных строим сетевой график проекта (рис 2.4.15).
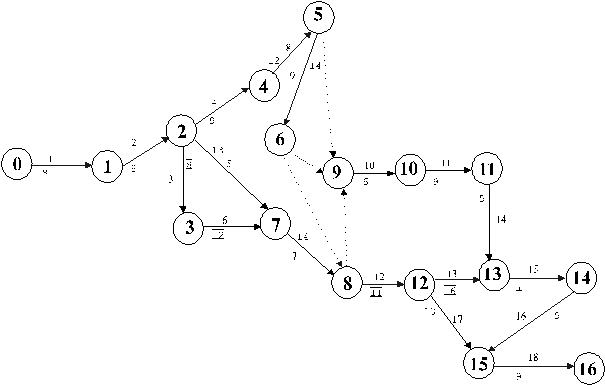 Рисунок 2.4.15
Рисунок 2.4.15
События пронумерованы в кружках, линии со стрелками – работы. Рядом со стрелками-работами стоят их номера и (с черточками над и под числом) продолжительность. Пунктиром выделены фиктивные работы.
Затем рассчитаем наиболее ранние возможные сроки наступления событий и наиболее поздние допустимые сроки наступления событий (рис. 2.4.16). Наиболее ранние возможные сроки наступления событий отображены в квадратиках рядом с самим событием, над квадратиками расположены наиболее поздние допустимые сроки наступления событий. Выделяем на графике критические работы, из которых складывается критический путь. Критический путь составляют работы: 1,2,4,8,9,(из 6 до 8 события фиктивная работа),12,13,15,16,18 – эти работы выделены другим цветом на графике (рис. 2.4.16). Критическое время выполнения проекта –104.
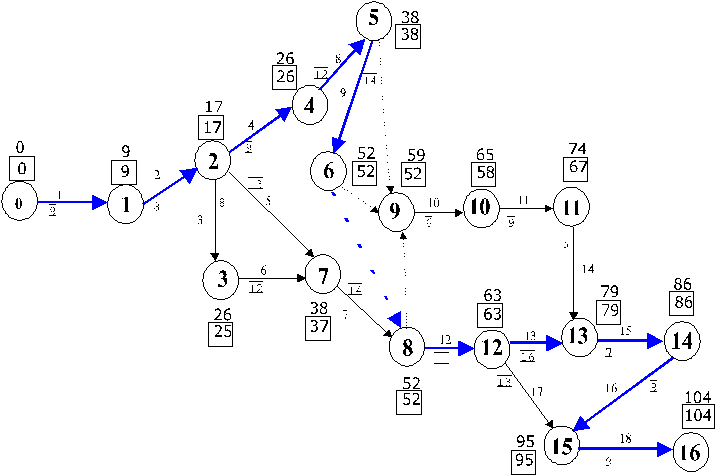 Рисунок 2.4.16
Рисунок 2.4.16
Теперь вычислим резервы времени для некритических операций. Рассчитанные резервы времени внесем в табл. 2.4.6.
Таблица 2.4.6
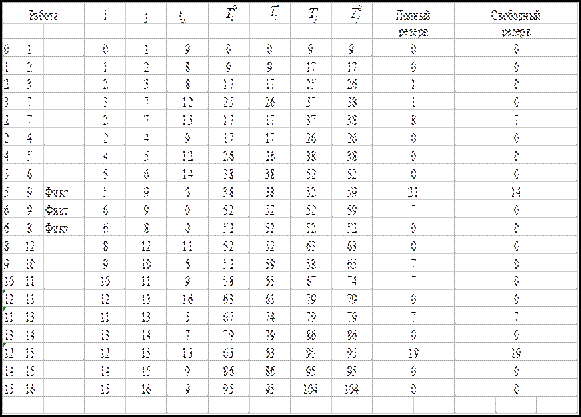 Теперь преобразуем полученную таблицу к виду (таблица 2.4.7), необходимому для построения календарного графика проекта. Введем в таблицу для каждой работы срок позднего начала и срок раннего окончания. Также добавим графу, указывающую на потребности в ресурсах каждой работы.
Теперь преобразуем полученную таблицу к виду (таблица 2.4.7), необходимому для построения календарного графика проекта. Введем в таблицу для каждой работы срок позднего начала и срок раннего окончания. Также добавим графу, указывающую на потребности в ресурсах каждой работы.
Таблица 2.4.7
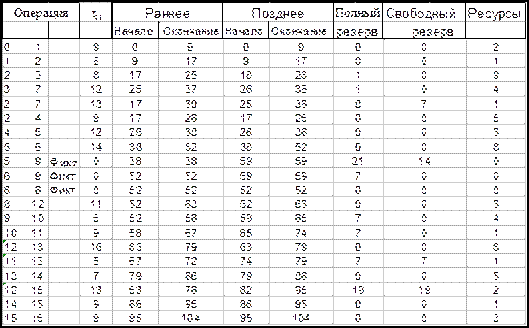
На основе полученной таблицы строим календарный график реализации проекта (рис 2.4.17) и два графика ресурсных профилей проекта - в первом выберем в качестве моментов начала некритических работ их ранние возможные сроки, получим ранний календарный план реализации проекта (рис 2.4.18), а во втором выберем в качестве моментов начала некритических работ их поздние допустимые сроки, получим поздний календарный план реализации проекта (рис 2.4.19)
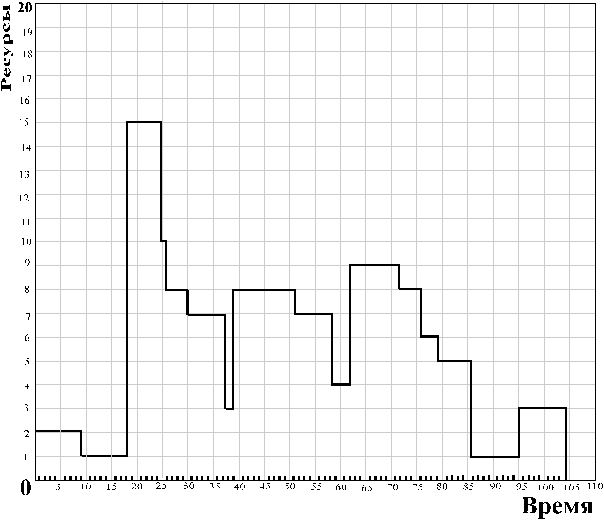 Рис 2.4.18
Рис 2.4.18
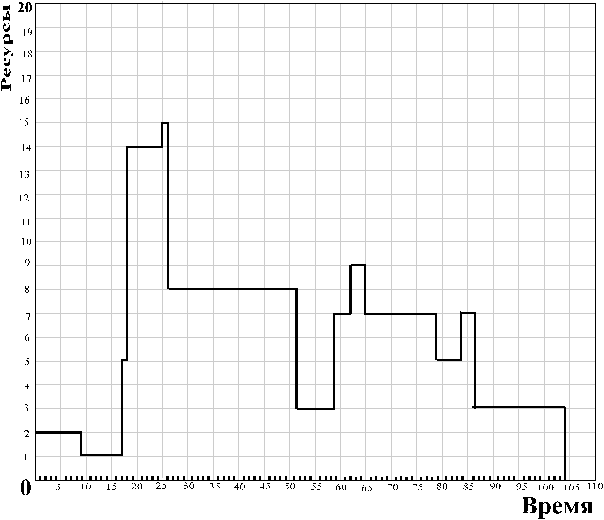 Рис 2.4.19
Рис 2.4.19
Максимальная потребность в ресурсах, как на раннем, так и на позднем календарных планах равна 15, но на позднем календарном плане время использования максимума ресурсов составляет 1, а на раннем плане 8. Также из графиков видно, что наиболее равномерно ресурсы распределены на позднем плане. Поэтому наиболее оптимальной реализацией проекта (их этих двух рассматриваемых вариантов) будет поздний календарный план. Передвигая сроки начала у некритических работ (в пределах резервов времени) можно добиться еще более равномерного использования ресуссов[1].
Тесты
1. Главными элементами сетевой модели являются:
а) игровые ситуации и стратегии;
б) состояния и допустимые управления;
в) события и работы.
2. В сетевой модели не должно быть:
а) контуров и петель;
б) собственных векторов;
в) седловых точек.
3. Критическим путем в сетевом графике называется:
а) самый короткий путь;
б) самый длинный путь;
в) замкнутый путь.
4. Математической основой методов сетевого планирования является:
а) аналитическая геометрия;
б) теория электрических цепей;
в) теория графов.
5. Оптимизация сетевого графика методом время-стоимость позволяет:
а) сократить стоимость реализации проекта;
б) сократить время реализации проекта;
в) найти зависимость стоимости проекта от времени его реализации.
6. Из приведенного ниже списка выберите те задачи, для решения которых можно применить метод критического пути.
а) Все виды строительных и ремонтных работ.
б) Программа переоснащения станочного парка для массового производства.
в) Календарное планирование мелкосерийного производства.
г) Процедура запуска исследовательской ракеты.
д) Планирование бюджета.
е) Мобилизация, стратегическое и тактическое планирование.
з) Освоение новой продукции.
и) Сборка и испытания электронных систем.
к) Монтаж, программирование и отладка программ вычислительных систем.
л) а,б,д,е,з;
м) все вышеперечисленные;
н) а,б,е-к;
о) б,в,г,д,к;
п) в,д,и,к.
7. Что необходимо знать для применения методов “критического пути”?
а) информацию о требуемой последовательности выполнения операций;
б) информацию о продолжительности каждой операции;
в) информацию о затратах;
г) содержание п. а-в;
д) содержание п. а,б.
8. Критическое время это:
а) отставание от директивго срока;
б) длина критического пути;
в) крайний срок начала проекта.
9. При оптимизации сетевого графика используются:
а) полные и свободные резервы работ;
б) расположение объекта;
в) время начала проекта.
10. Что не относится к временным параметрам работ?
а) свободный резерв;
б) полный резерв;
в) скрытый резерв.
Ответы к тестам
| 1) в | 6) н |
| 2) а | 7) г |
| 3) б | 8) б |
| 4) в | 9) а |
| 5) в | 10) в |
Контрольные вопросы
1. Указать основные элементы сетевой модели.
2. Каковы правила построения сетевых моделей?
3. Каков принцип оптимизации задач сетевого планирования?
4. Последовательность построения сетевых графиков.
5. Алгоритм расчета временных параметров сетевой модели.
6. Идея оптимизации потребления ресурсов при управлении проектами.
7. Область применения сетевых моделей.
Задания и задачи
Задача 1. Построить сетевую модель и календарный график выполнения работ и потребления ресурсов по указанным в таблице данным.
График построить в двух вариантах: в ранние и поздние сроки начала работ – сделать выводы.
| Номера работ (операций) | Каким работам предшествует | Продолжительность работ | Потребность в трудресурсах |
| 2, 3 | |||
| 4, 5 | |||
| 6,7,9 | |||
| 10, 11, 12 | |||
| 9, 10 | |||
| 10, 12 | |||
| 11,13 | |||
| 14,15 | |||
| 13, 17 | |||
| 15,16 | |||
| 15,17 | |||
Задача 2. Компания «АВС» реализует проект производства некоторого изделия. Перечень работ проекта и их характеристики представлены в таблице.
Таблица. Перечень работ и их характеристики
| Работы | Непосредственно предшествующие работы | Продолжительность работы, недель | Трудоемкость работы |
| A | - | ||
| B | - | ||
| C | - | ||
| D | A | ||
| E | C | ||
| F | B, E | ||
| G | C | ||
| H | F, G | ||
| I | F | ||
| J | D,I | ||
| K | F | ||
| L | F | ||
| M | K | ||
| N | H,L | ||
| O | K | ||
| P | K | ||
| R | J, O | ||
| S | P, N |
Задание:
1. Изобразить проект с помощью сетевой модели.
2. Найти критический путь, ожидаемую продолжительность выполнения проекта, временные характеристики работ.
3. Разработать график реализации проекта и потребления ресурсов.
Задача 3. Выполнить расчет временных параметров сети.
Вычертить календарный график работ в ранние сроки (линейную диаграмму). Исходные данные заданы сетевым графиком.
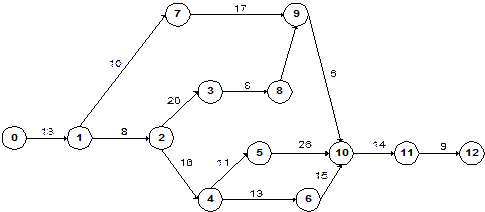
Задача 4. Изобразить проект с помощью сетевой модели. Выполнить расчет временных параметров сети. Вычертить календарный график работ в ранние сроки. Исходные данные заданы в таблице.
| Коды работ | Длительность работ (дни) |
| 1-2 | |
| 2-3 | |
| 3-8 | |
| 1-4 | |
| 4-6 | |
| 4-7 | |
| 6-7 | |
| 7-8 | |
| 1-5 | |
| 5-8 | |
| 2-4 | |
| 5-6 |
Задача 5. Построить сетевую модель, вычислить все основные характеристики работ и событий. Найти критический путь и его продолжительность.
| Работа | a | b | c | d | e | f | g | h | i | j | k | l | m | n | p |
| Непосредственный предшественник | – | – | – | – | a | c, h | c, h | d | b, e, f | b, e, f | i, l | j, g | j, g | m | j, g |
| Продолжительность |
Дата добавления: 2020-10-25; просмотров: 1111;











