Складання центрованих оптичних систем. Телескопічна система

Звично окремі частини оптичних приладів (об’єктиви, окуляри) складаються із декількох лінз, які створюють центровану систему з загальною оптичною віссю. Складна центрована система складається, таким чином, із декількох простих систем – лінз, що мають заломлюючі поверхні і визначаються своїми головними площинами і фокусами. Таку складну систему із декількох лінз замінюють еквівалентною, визначивши для її положення головних площин і фокусів. Еквівалентна система має на відміну від простої не одну, а дві головні площини: передню і задню. Відшукування головних площин і фокусів еквівалентної системи по заданих відповідних елементах простих систем називають складанням систем. Відрізок D оптичної осі між заднім фокусом першої системи і переднім фокусом другої системи називають оптичним інтервалом. Із рис. 2.18 маємо, що

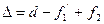(2.44)

Представимо на рис. 2.18 складну оптичну систему з двох сферичних поверхонь. Перша система задається положенням головних площин Н₁ і Н’₁, переднього і заднього фокусів, а друга – відповідно положення Н₂ і Н’₂, F₂ F’₂. Відстань між головною площиною першої і переднього головного площиною другої системи H’₁H₂=d.

Промінь Р з простору променів, паралельний оптичній осі, заломиться в точці М’₁, пройде через задній фокус першої системи і заломиться другими головними площинами Н₂ і Н’₂ в точках N₂ і N’₂. Після перетину з оптичною віссю в точці F’, що називається заднім головним фокусом еквівалентної системи, промінь зустрічається з геометричним продвиженням свого вихідного напряму в точці М’. Перпендикуляр до оптичної осі в точці М’ називається задньою головною площиною еквівалентної системи. Позначимо положення заднього головного фокусу другої системи величиною F’, а відносно задньої головної площини Н’– величиною f’_e, що називається задньою фокальною відстанню еквівалентної системи.

Аналогічно промінь Р з простору зображень, паралельний оптичній осі, заломиться в точці М₂, пройде через передній фокус F₂ другої системи і заломиться головними площинами першої системи Н’₁ і Н₁ в точках N’₁ i N₁. Після перетину з оптичною віссю в точці F, що називається переднім головним фокусом еквівалентної системи, промінь зустрічається з геометричним продовженням свого вихідного напряму в точці М. Перпендикуляр до оптичної осі в точці М називається передньою головною площиною еквівалентної системи. Позначимо положення переднього головного фокусу еквівалентної системи величиною c_F, а відносно передньої головної площини Н – величиною f_e, що називається передньою фокальною відстанню еквівалентної системи.

Положення переднього і заднього фокусів еквівалентної оптичної системи, а також фокальні відстані визначається за формулами 16.

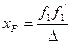(2.45)

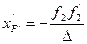(2.46)

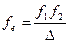(2.47)

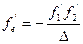(2.48)

Із рис. 2.18 видно, що

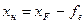(2.49)

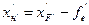(2.50)

Підставимо в (2.49) і (2.50) відповідні значення із (2.45) 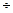(2.48), будемо мати

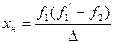(2.51)

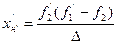(2.52)

Формули (2.51) і (2.52) дозволяють визначити положення головних площин еквівалентної оптичної системи.

Відстань між головними площинами еквівалентної оптичної системи визначається за формулою:

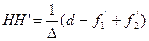(2.53)

Еквівалентна оптична система може бути повністю охарактеризована чотирма по різному сполученими величинами:

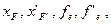(2.54)

або

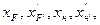(2.55)

або

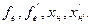(2.56)

Іншими словами, люба оптична система може бути представлена положеннями: оптичної осі, передньої і задньої головних площин, а також переднього і заднього головних фокусів.

Для геодезичних приладів особливо важливі телескопічні системи. Телескопічною або фокальною системою називають систему, в якій оптичний інтервал D=0, тобто задній фокус першої системи збігається з переднім фокусом другої. Фокальні відстані телескопічної системи згідно (2.47) і (2.48) дорівнюють

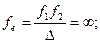
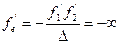(2.57)

Таким чином до телескопічних систем відносять зорові труби, що сфокусовані на нескінченність для нормального ока. Це означає, що паралельний пучок променів після заломлення в оптичній системі залишається паралельним. Відповідно до (2.51) і (2.52) головні площини оптичної системи будуть також знаходитись в нескінченності

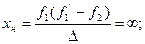
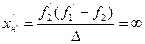(2.58)

В телескопічних системах з паралельним пучком променів апертурною діафрагмою буде оправа об’єктива. Вона ж буде і вхідною зіницею (D_об.). Зображення цієї діафрагми в просторі зображень буде вихідною зіницею (d_ок) оптичної системи. Відношення

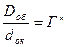(2.59)

називається кутовим збільшенням оптичної системи, а відношення

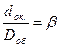(2.60)

називається лінійним збільшенням оптичної системи.

Література.

1. Боровий В.О. Автоколімаційні, поляризаційні і лазерні вимірювання в геодезії : Монографія. Чернігів, РВВ- ЧДІЕіУ- НЦ МДВУ, 1999, - 231с.

2. Кузнецов П.Н., Васютинский Н.Ю., Ямбаев Х.К. Геодезическое инструментоведение: Учебник для вузов. – М.: Недра, 1984,- 364с.

3. Островский А.Л., Маслюч Д.И., Гребенюк В.Г. Геодезическое прибороведение. Львов. Вища школа, 1983.- 205с.

4. Костецька Я.М. Геодезичні прилади. Частина ІІ. Електронні геодезичні прилади: Підручник для студентів геодезичних спеціальностей вузів. – Львів: ІЗМН, 2000- 324 с.

5. Літнарович Р.М. Польовий компаратор ЧДІЕіУ. Чернігів, ЧДІЕіУ, 2002, - 16 с.

6. Літнарович Р.М., Мардієва Л.П., Ярош Ю.В. Будова і робота світловіддалеміра СТ5. Навчальний практикум по курсу “Електронні геодезичні прилади”, ЧДІЕіУ,Чернігів,2000, - 38 с.