Понятие об учете неритмичности движения автомобилей

Число автомобилей-самосвалов определяется достаточно просто, если предполагается, что они работают в постоянном ритме и подходят к экскаватору через равные промежутки времени; к моменту очередной погрузки у экскаватора оказывается свободный автомобиль-самосвал. В действительности процесс протекает много сложнее.

Даже если средняя скорость движения каждого автомобиля, равная расчетной, может считаться постоянной, фактические скорости в данный момент времени по случайным причинам претерпевают колебания и автомобили движутся не на равных, а на меняющихся расстояниях один от другого. Они то приближаются, то удаляются друг от друга и подходят к экскаватору в неравные промежутки времени.

Если последние оказываются меньше времени погрузки, у экскаватора образуется очередь свободных автомобилей-самосвалов. В противном случае экскаватор некоторое время будет простаивать в ожидании запаздывающих автомобилей-самосвалов.

Если средняя скорость автомобилей одинакова, говорят о стационарности потока. Стационарные потоки характеризуются постоянной, независимой от времени средней плотностью событий — появлением на любом отрезке дороги или в промежутке времени постоянного числа р_а автомобилей.

Обычно автомобили не обгоняют один другого, а движутся поодиночке. Поэтому в любом достаточно малом промежутке времени может появиться только один автомобиль. Это свойство потока называется ординарностью. Расположение автомобилей на одном участке дороги в общем не зависит от их расположения на другом участке. Это свойство потока выражает так называемое отсутствие последействия и позволяет считать появление или непоявление автомобиля событиями независимыми.

В теории вероятностей доказывается, что потоки, обладающие свойствами стационарности, ординарности и отсутствия последействия, или простейшие потоки подчиняются закону распределения Пуассона, поэтому их называют также пуассоновскими. При типичных для рассматриваемых условий параметрах пуассоновского потока вероятность простоя экскаватора по причине отсутствия автомобилей-самосвалов оказывается значительно выше вероятности практически одновременного подхода двух и более машин.

Следовательно, высокая плотность загрузки экскаватора и автомобилей-самосвалов, вытекающая из кажущейся очевидной в своей целесообразности предпосылки их жестко согласованной, равномерной работы, при наличии случайных колебаний скорости движения оборачивается существенным снижением производительности экскаватора, вызываемым запаздыванием машин.

В действительности приходится иметь дело еще и с колебаниями времени погрузки, случайным характером пропускной способности экскаватора. Исследование систем подобного рода относится к области математической теории массового обслуживания, но некоторые простейшие задачи можно проанализировать и не прибегая к аппарату этой теории.

Допустим, экскаватор способен обслуживать стационарный поток плотностью р_ан а рассчитывается на поток с меньшей плотностью р_аэ. Отношение

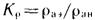
выражает в долях единицы степень использования экскаватора или его занятости, иначе говоря, вероятность того, что экскаватор будет работать на погрузке автомобилей-самосвалов. Очевидно, часть времени (1 — К_Р) экскаватор окажется свободным. Чем меньше K_р тем успешнее экскаватор ликвидирует очереди, но тем дольше доля потерь времени вследствие собственных простоев экскаватора.

Чем больше К_р тем лучше используется экскаватор, но тем вероятнее образование очередей, больше их длина и потери времени автомобилей-самосвалов в ожидании обслуживания. Экскаватор пропускает в среднем за единицу времени р_аэ автомобилей-самосвалов и не в состоянии обслужить из-за простоев в среднем р_ан(1 — К_р) машин. Количество погруженных машин на одну машину неиспользованного резерва даст среднюю длину очереди

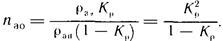
Поскольку автомобиль-самосвал грузится в среднем за время 1/р_аэ время ожидания в очереди:

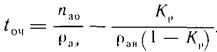
Его нужно прибавлять к времени цикла автомобиля-самосвала, которое должно учитывать и среднее время ожидания погрузки. Таким образом, полное число автомобилей-самосвалов с учетом времени ожидания в очереди у экскаватора

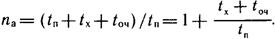
Расчеты количества автомобилей-самосвалов с учетом очередей имеют технико-экономический характер. Нужно, к примеру, решить, что целесообразнее: увеличить производительность комплекта за счет снижения простоев экскаватора и роста численности автомобилей-самосвалов или ограничить последнюю и ориентироваться на несколько заниженную производительность, что, естественно, влияет на общий срок работ.

Вопросы подобного рода выходят за рамки технологии и рассматриваются в курсе организации строительства. В технологических расчетах число автомобилей определяют без учета ожиданий, поскольку многие расчетные характеристики осреднены, ориентировочны, а результаты расчета при необходимости довольно просто корректируются по данным практики.