Критерий по асимметрии и эксцессу
Некоторые признаки растений, животных и микроорганизмов при объединении объектов в группы дают распределения, значительно отличающиеся от нормального.
В тех случаях, когда какие-нибудь причины благоприятствуют появлению значений признака, отличающихся от средней величины в сторону уменьшения или увеличения, образуются асимметричные распределения. При асимметрии эмпирическое распределение имеет увеличенные (против симметричного расположения) частоты в левой или правой части. В соответствии с этим различают или левую (положительная), или правую (отрицательная) асимметрию.
В тех случаях, когда какие-нибудь причины благоприятствуют преимущественному появлению и средних, и крайних значений признака, образуются положительные эксцессивные распределения, имеющие вид острой пирамиды с расширенным основанием. При отрицательном эксцессе в центре распределения имеется не вершина, а впадина, причем распределение становится двумодальным, а вариационная кривая – двувершинной.
В некоторых исследованиях требуется выяснить, действительно ли распределение изучаемого признака имеет асимметрию или эксцесс.
Например, при изучении ареалов распространения морских животных можно предположить, что распределение особей этого вида по глубине обитания должно быть, асимметричным, так как свободному распространению его водном из направлений – вверх – препятствует естественная граница: поверхность моря. Это предположение можно проверить, исследовав степень асимметричности распределений. Наличие эксцессивного распределения одного из жизненно важных признаков изучаемого вида животных или растений может указать на тенденцию этого вида образовывать не только обычные, типичные формы, также давать в повышенном количестве новые для него вариации, сильно отклоняющиеся от нормы.
Для выяснения достоверности того, что изучаемое распределение отличается от нормального именно в сторону асимметрии или эксцесса, применяют обычный в биометрии метод сравнения показателей с их ошибками репрезентативности.
Показатели асимметрии и эксцесса с их ошибками репрезентативности определяются по следующим формулам:
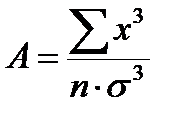 ;
; 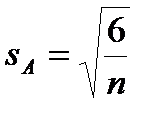 ;
; 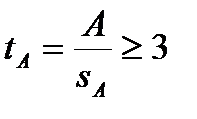 ; (8.4)
; (8.4)
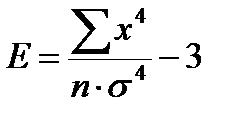 ;
; 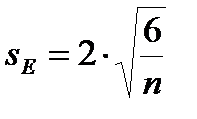 ;
; 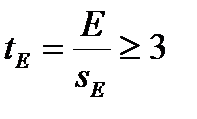 , (8.5)
, (8.5)
где А – показатель асимметрии;
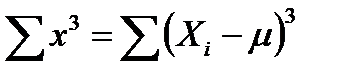 – сумма кубов отклонений от средней арифметической (центральных отклонений);
– сумма кубов отклонений от средней арифметической (центральных отклонений);
s3 – стандартное отклонение, возведенное в третью степень;
Е – показатель эксцесса;
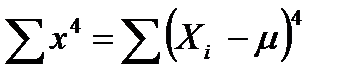 – сумма четвертых степеней центральных отклонений;
– сумма четвертых степеней центральных отклонений;
s4 – четвертая степень среднего квадратического отклонения;
n – общее число данных в эмпирическом распределении;
sA, sE – ошибки репрезентативности показателей асимметрии и эксцесса;
tA, tE – критерии достоверности выборочных показателей асимметрии и эксцесса.
Показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирических распределений от нормального в том случае, если они превышают свою ошибку репрезентативности в три и более раз.
Вопросы для самоконтроля
1 Что является определяющим при составлении вариационного ряда: количество относительно одинаковых значений признака или само его значение?
2 Чем отличается построение гистограммы от графического изображения?
3 Какие значения указываются на осях координат при построении графика вариационных кривых?
4 Чему равны первое и последнее значения кумуляты?
5 Определение критерия χ2.
6 При каких условиях значений критерия χ2 нулевая гипотеза опровергается или подтверждается?
7 Определение критерия λ.
8 Каково условие при применении критерия лямбда по количеству данных?
9 Какой из критериев χ2 или λ обладает большей мощностью (чувствительностью)?
10 При каком условии показатели асимметрии и эксцесса свидетельствуют о достоверном отличии эмпирического распределения от нормального?
ТЕМА 9 Нормальное распределение
9.1 Генеральная совокупность и выборка
9.2 Репрезентативность
9.3 Ошибки репрезентативности и другие ошибки исследований
9.4 Доверительные границы
Привлечение объектов для исследования можно проводить двумя основными методами. Можно подвергнуть изучению всех особей определенного массива или только их часть, определенным образом выбранную. В первом случае проводится сплошное обследование всей генеральной совокупности, во втором случае – выборочное исследование.
Дата добавления: 2020-10-25; просмотров: 617;











