Определение ускорения при свободном падении

Для нахождения величины g используются сведения, приобретенные учащимися при изучении прямолинейного равномерного и равномерно-переменного движения,- работы и энергии. Вывод окончательного выражения для определения ускорения при свободном падении требует знания геометрической прогрессии, изучаемой в курсе математики средней школы.

Лабораторную работу по определению g целесообразно поставить в одном из трех случаев: 1) при повторении курса физики; 2) в практикуме X класса; 3) в порядке кружковой работы. Можно также предложить отдельным ученикам X класса, успешно справившимся с выполнением лабораторной работы «Определение ускорения силы тяжести с помощью маятника» по теме «Колебания», измерить g другим способом, а затем сравнить полученные результаты и оценить точность измерения в обоих случаях.

Предлагаемый способ определения ускорения свободного падения требует наличия следующего оборудования: секундомера; металлического шарика диаметром 0,8—1 см; гладкой гранитной плиты размером 300 х 300 мм; двухметровой линейки с делениями; уровня.

Гладкая гранитная плита с помощью уровня устанавливается строго горизонтально. Металлический шарик, поднятый на высоту 1,2—1,5 м, свободно падает на гранитную плиту. Ударившись, он подпрыгивает, падает на плиту, снова подпрыгивает и т. д. Рассмотрим движение шарика с момента первого удара. Отскочив от плиты, шарик подымается на высоту h₁ (рис. 1), двигаясь равнозамедленно с ускорением g, а потом падает с высоты h₁ с таким же ускорением. При этом между двумя последовательными ударами о плиту шарик проходит отрезки, равные 2h₁ 2h₂, ... и т. д.

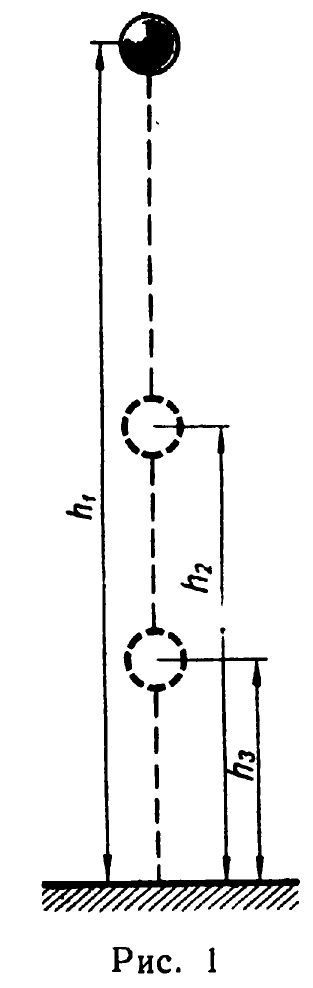
Весь путь, пройденный шариком за n + 1 удар о плиту, равен: s — v_cp т, где v_cp — средняя скорость движения шарика (среднее значение из абсолютных значений скоростей), а т — время между первым и n +1 ударами шарика о плиту (определяется с помощью секундомера). Так как отсчет пути идет с момента первого удара, то при n + 1 ударах v_cp =

- средние скорости движения шарика на путях

Не трудно установить, что Здесь - промежутки времени, за которые шарик проходит соответственно пути

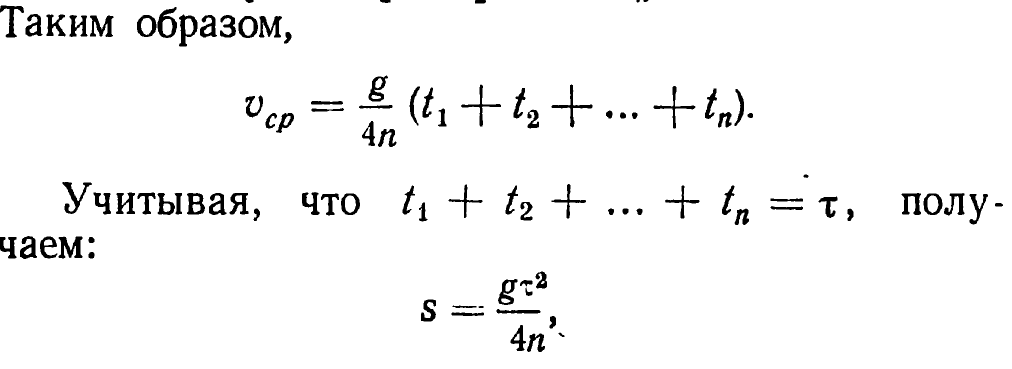
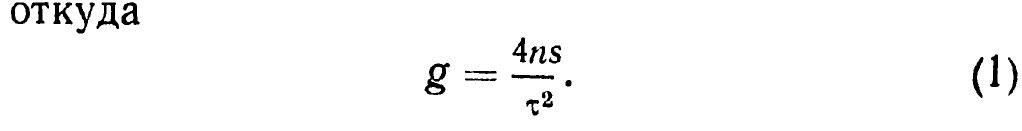
Причем, s = 2h₁ + 2h₂ +... + 2h_n; h₁ … h_n находим по известной величине h (высота, на которую сначала был поднят шарик над гранитной плитой) и коэффициенту отражения шарика k. Коэффициент k определяется с помощью соотношения где Н — высота, с которой шарик падает, а H₁ — высота, на которую он подымается после удара. Желательно коэффициент k определить несколько раз для различных высот Н и вычислить среднее арифметическое значение. Таким образом, для s получаем следующее соотношение: s = 2hk + 2hk² + … + 2hkⁿ, или s = 2h (k + k² + … + kⁿ).

Выражение в скобках представляет собой сумму геометрической прогрессии. Следовательно

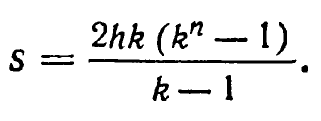
Подставляя это значение в выражение (1), получим окончательную формулу для определения величины ускорения при свободном падении:

Если в физическом кабинете школы не окажется приборов и предметов, рекомендуемых в статье, то их можно заменить другими. Точность определения ускорения силы тяжести останется достаточно высокой, вполне удовлетворяющей требованиям, предъявляемым к школьной лабораторной работе. Гранитную плиту можно заменить гладкой полированной доской, а металлический шарик — мячиком для игры в настольный теннис.

Для определения коэффициента отражения k следует воспользоваться линейкой с делениями длиной 1,2—1,5 м, так как при больших высотах падения начинает сказываться сопротивление воздуха.

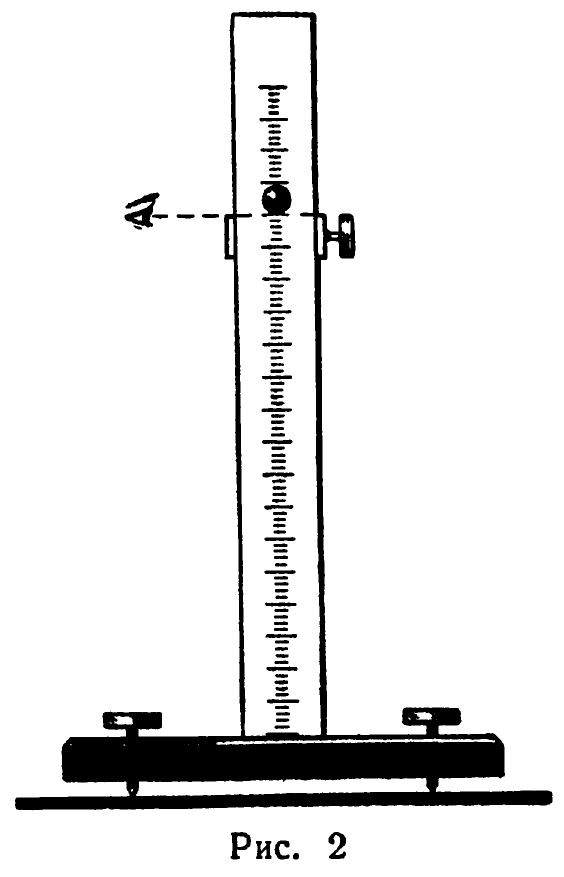
Для достижения большей точности в определении значения k можно порекомендовать простое приспособление для фиксирования положения шарика в верхней точке после удара. Оно состоит из стойки, вдоль которой могут перемещаться две параллельные планки, причем планки устанавливаются на одном уровне перпендикулярно к стойке (рис. 2).

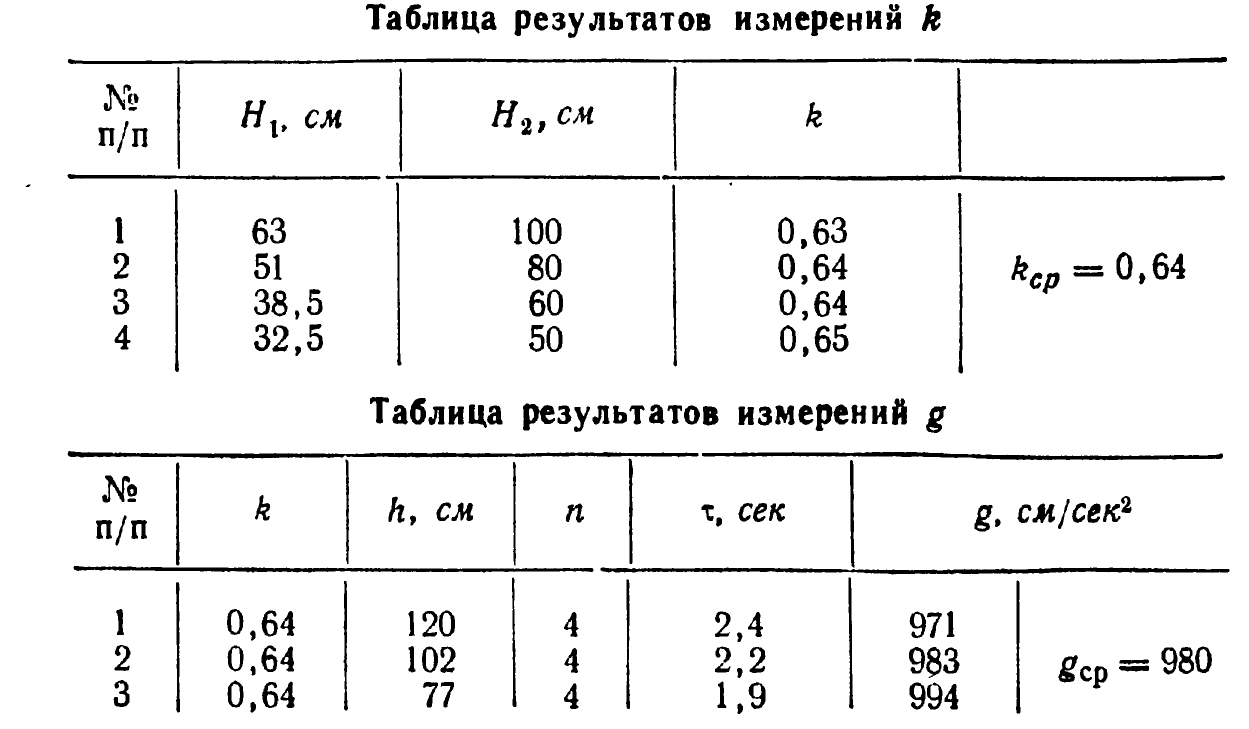
Ниже приведены результаты нескольких измерений величины k и g, в которых были использованы теннисный шарик и гладкая деревянная доска.