собственных векторов

Нахождение собственных значений путем решения характеристического полинома можно назвать прямым способом. Существуют и итерационные способы, например, для положительно определенной симметрической матрицы, часто встречающейся в практических приложениях, известен итерационный способ одновременного нахождения собственных значений и собственных векторов.

Напомним свойства положительно определенной симметрической матрицы:

1) все собственные числа действительны и положительны;

2) собственные векторы образуют систему ортогональных полиномов, то есть

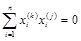при j ¹ k . (4.22)

Рассмотрим систему линейных уравнений (4.18). Для определения собственных векторов x⁽ⁱ⁾, соответствующих всему спектру собственных значений {l_i}, имеем n систем уравнений:

Ах⁽¹⁾=l₁х⁽¹⁾; Ах⁽²⁾=l₂х⁽²⁾; …, Ах⁽ⁿ⁾=l_nх⁽ⁿ⁾, (4.23)

каждая из которых представляет собой систему n нелинейных уравнений с n+1 неизвестным.

Преобразуем первую систему из этого списка (запишем справа налево и поделим на l₁):

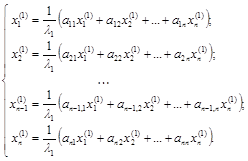
Теперь воспользуемся тем обстоятельством, что при умножении (делении) собственного вектора на скаляр он остается собственным вектором той же матрицы, то есть он определяется с точностью до коэффициента пропорциональности. Отсюда практический вывод: собственный вектор можно нормировать, например, поделив на максимальный элемент. Таким образом, можно всегда положить одну из координат собственного вектора равной единице. Пусть х_n⁽¹⁾ = 1.

Для решения получившейся системы n нелинейных уравнений с n неизвестными можно использовать, например, метод простой итерации.

Итерационный процесс будет иметь вид:

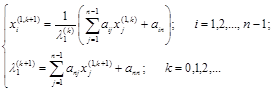
Задаем начальные приближения и и с заданной степенью точности находим первое собственное значение l₁ и первый собственный вектор х⁽¹⁾.

Для нахождения второго собственного значения l₂ и второго собственного вектора х⁽²⁾ запишем вторую систему из списка (4.23):

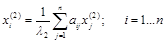(4.24)

и воспользуемся условием ортогональности (4.22), записав его для векторов х⁽¹⁾ и х⁽²⁾:

.

Выразим отсюда одно из неизвестных, например, :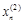

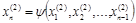
и, подставляя его в (4.24), получаем

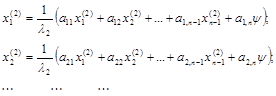
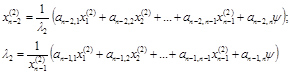
Полагая 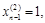решаем эту систему методом простой итерации и получаем второе собственное значение l₂ и второй собственный вектор

.

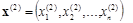Для нахождения третьего собственного значения l₃ и второго собственного вектора 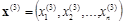записываем два соотношения ортогональности:

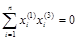, из которого выражаем 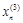, и

, и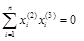з которого выражаем .

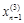Добавляя условие нормализации 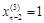, решаем третью систему уравнений из списка (4.23). И так далее.

Так как собственные векторы определяются с точностью до коэффициентов пропорциональности, то решение будет выглядеть следующим образом:

l1			…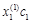
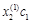
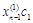
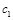
l2			…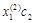
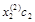
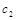
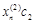
l3			…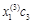
…	…	…	…	…	…
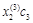
ln			…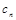

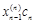
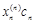
[1] Так как условие ||B||<1 – достаточное условие сходимости, то практически можно поступить следующим образом. После преобразования программируем итерационную схему и проводим вычисление. Если процесс сходится – решение найдено, если нет – проводим другое преобразование.

[2] Например, для квадратного уравнения l²+р₁l+р₂=0, используя теорему Виета, получаем формулу Ньютона при k=1: S₁= l₁+l₂ =-p₁ Далее, рассмотрим S₂=l₁²+l₂²= =(l₁+l₂)²-2l₁l₂ =(-p₁)(-p₁)-2p₂ . Заменяя –p₁=l₁+l₂ =S₁, получаем формулу Ньютона при k=2 : S₂+p₁S₁=-2p₂.

[3] Англ. trace – след, или нем. Spur - след