Использование диаграмм для решения прикладных задач
Основным предназначением диаграмм является наглядное отображение табличных данных и отслеживание соотношений между ними. Данное качество может быть применимо для построения и исследования графиков функций, решения систем уравнений, выполнения задач анализа и т.п.
Сказанное продемонстрируем на примерах.
На рис. 4.41 показан график функции y = x2.
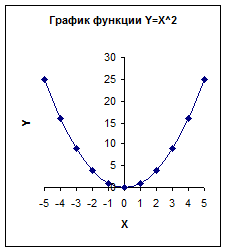 Как видно из графика, Excel установил различные единичные отрезки по осям абсцисс и ординат.
Как видно из графика, Excel установил различные единичные отрезки по осям абсцисс и ординат.
Выделив диаграмму и захватив ее граничные маркеры, можно попытаться исправить данный недостаток. Хотя, с другой стороны, это является и достоинством.
Рис. 4.41. График функции,
построенный средствами Excel
Построению графика функции предшествовало создание таблицы (рис. 4.42).

Рис. 4.42. Фрагмент электронной таблицы с данными
для построения графика y=x2
Затем после выделения таблицы (ячеек А2:L3) были выполнены команды:
Кнопка Мастер диаграмм ® Вкладка Стандартные ®
Тип диаграммы Точечная ® Вид диаграммы:
со значениями, соединяющимися сглаживающими линиями ®
Кнопка Далее> ® Кнопка Далее> ® Вкладка Заголовки ®
Ввод названия диаграммы ® Ввод заголовка оси Х ®
Ввод заголовка оси Y ® Вкладка Линии сетки ®
Снять флажки линий сетки ® Вкладка Легенда ®
Снять флажок Добавить легенду ® Кнопка Далее> ®
Поместить диаграмму: на имеющемся листе ® Кнопка Готово
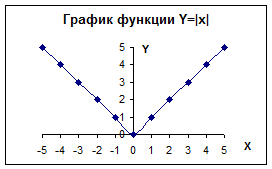 Изменив формулу для вычисления ординаты функции, например, на y=|x|, получим новый график. В нем после построения дополнительно были перемещены надписи заголовков осей и изменена их шкала (рис. 4.43).
Изменив формулу для вычисления ординаты функции, например, на y=|x|, получим новый график. В нем после построения дополнительно были перемещены надписи заголовков осей и изменена их шкала (рис. 4.43).
Примечание.
При построении, например, функции y=1/x следует удалить значение ординаты для значения x=0, так как в этой точке происходит разрыв функции.
Представляет интерес и решение физических задач.
Пусть требуется определить дальность D и время полета T материальной точки, брошенной под углом a к горизонту с начальной скоростью V0, а такжемаксимальную высоту ее подъема H. Необходимо также показать траекторию полета в координатах Х0У и зависимость высоты от времени полета.
Пусть a = 300, V0 = 20 м/c, g = 9,8 м/c2.
Для решения первой части данной задачи используются формулы:
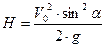 , ,
| 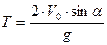 , ,
| 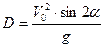
|
Введя данные формулы в ячейки электронной таблицы, найдем, что H » 5,1 м, T » 2,04 c, D » 35,3 м.
Для нахождения траектории полета следует из уравнения движения материальной точки исключить время t:
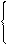 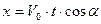
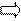 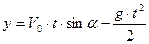
| 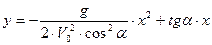
|
Затем необходимо построить таблицу (рис. 4.44). В ней необходимо предусмотреть, что аргумент тригонометрических функций должен быть указан в радианах. Построение требуемых графиков (рис. 4.45, 4.46) выполняется наподобие ранее описанных.
| A | B | C | D | E | F | G | H | I | J | K | L | M | |
| g, м/c2 | 9,8 | ||||||||||||
| V0, м/c | |||||||||||||
| a, град | |||||||||||||
| a, рад | =D3*ПИ()/180 | ||||||||||||
| t | 0,2 | 0,4 | 0,6 | 0,8 | 1,2 | 1,4 | 1,6 | 1,8 | 2,04 | ||||
| x | 3,5 | 6,9 | 10,4 | 13,9 | 17,3 | 20,8 | 24,2 | 27,7 | 31,2 | 34,6 | 35,3 | ||
| y | 1,8 | 3,2 | 4,2 | 4,9 | 5,1 | 4,9 | 4,4 | 3,5 | 2,1 | 0,4 | 0,01 |
Рис. 4.44. Фрагмент электронной таблицы для построения графиков движения материальной точки
|
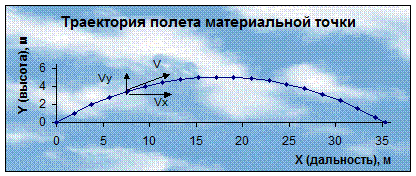
Рис. 4.45. Зависимость высоты полета
материальной точки от дальности
Примечания.
1. После копирования формул, по которым вычисляются текущие значения х и y, из диапазона В7:В8 в диапазон С7:М8 следует откорректировать в них ссылки на ячейки, в которых записаны исходные данные задачи, – a, V0 и g. В противном случае результат вычисления будет неверным.
2. График y=f(x) был построен после выделения диапазона А7:М8. Основой графика y=f(t) послужил диапазон несмежных ячеек А6:М6;А8:М8.
3. Для обоих графиков изменено оформление (шкалы осей координат, заливка, границы и линии сетки области построения, место и шрифт заголовков). На первый график в качестве заливки диаграммы выведен рисунок и нанесены стрелки с надписями.
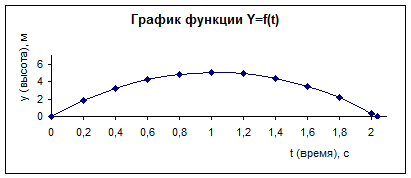
Рис. 4.46. График зависимости высоты полета материальной точки от времени
Дата добавления: 2020-10-25; просмотров: 637;











