Приведение системы сил к динаме

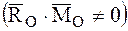
Определение: Система, состоящая из силы и пары сил, момент которой коллинеарен силе (плоскость пары перпендикулярна линии действия силы), называется динамой или динамическим винтом (рис. 30) .

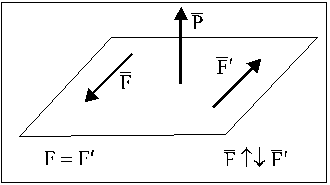
Рис. 30

Если при приведении системы сил к центру О второй инвариант не равен нулю, то эта система сил приводится к динаме (рис. 31).

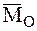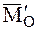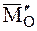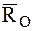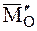Разложив на две составляющие - вдоль главного вектора и - перпендикулярно главному вектору, для и будем иметь случай 4.6.1б. Вектор 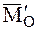, будучи свободным вектором, переносится параллельно самому себе в точку О₁):

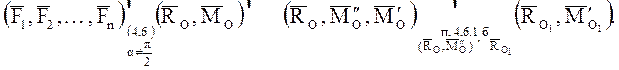Вектора 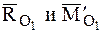представляют собой динаму,

где , .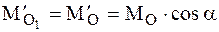

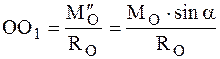В рассматриваемом случае приведения системы сил главный момент 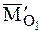имеет минимальное значение. Причем это значение момента сохраняется при приведении заданной системы сил к любой точке, лежащей на линии действия главного вектора 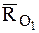и главного момента 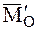(рис. 31). Уравнение этой линии, называемой центральной (осью динамы), определяется из условия коллинеарности векторов 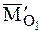и :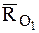

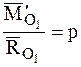. (4.27)

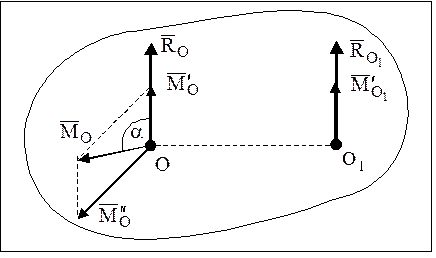
Рис. 31

В соответствии с соотношениями (4.16) и (4.17)

,

,

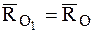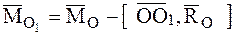тогда уравнение центральной оси динамы в векторной форме можно записать так:

.

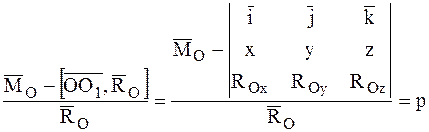Проектируя это соотношение на оси декартовой системы координат с началом в центре приведения О, получим:

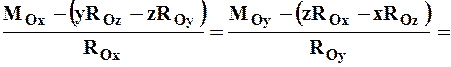
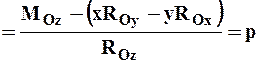. (4.28)

Здесь x, y, z – координаты точек, лежащих на центральной оси, а р – постоянная линейная величина, называемая параметром динамы.