Сложение взаимно перпендикулярных гармонических колебаний. Фигуры Лиссажу.

Пусть материальная точка одновременно участвует в двух колебаниях: одно направлено вдоль оси ОХ, другое — вдоль оси OY. Колебания зада­ны следующими уравнениями:

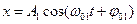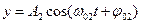; (4)

Допустим, что частоты колебаний одинаковы, т. е. ω₀₁ = ω_о2 = ω₀, тогда

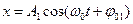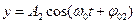; (5)

Уравнения (5) задают траекторию движения материальной точки в параметрической форме. Если в эти уравнения подставлять разные зна­чения t, то можно определить координаты х и у, а совокупность коорди­нат и есть траектория. Более наглядно траекторию можно представить в виде зависимости у = f(x), для получения которой следует исключить время из уравнений (5). Произведя математические преобразования, получим уравнение эллипса:

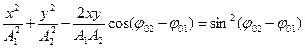. (6)

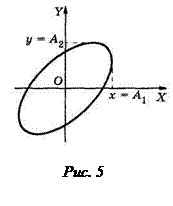Таким образом, при одновременном участии в двух взаимно перпен­дикулярных гармонических колебаниях одинаковой частоты, материаль­ная точка движется по эллиптической траектории (рис. 5).

Из выражения (6) вытекают следующие частные случаи:

1) 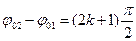, где k = 0, 1, 2, ….; 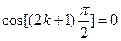, , 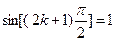тогда

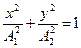(7)

Это каноническая форма уравнения эллипса, соответствующая сим­метричному расположению его относительно осей координат (рис. 6, а). Из (7) при A₁ = А₂ = R (рис. 6, б) получаем, как част­ный случай, уравнение окружности радиусом R:

x² + y² = R²; (8)

2) ) 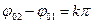, где k = 0, 1, 2, ….; 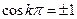, , 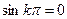тогда

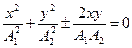, (9)

или после преобразований

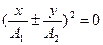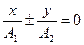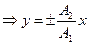, , (10)

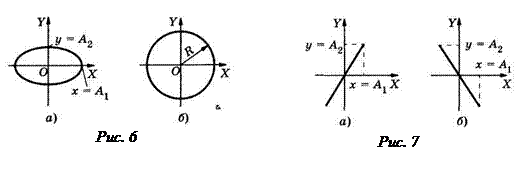
Это уравнение прямой, в которую вырождается эллипс (рисунку 7, а соответствует знак «+» в уравнении (10); рисунку 7, б — знак «-»).

При сложении взаимно перпендикулярных колебаний разных частот получаются различные траектории колеблющейся материальной точки, названные фигурами Лиссажу. Вид фигур Лиссажу зависит от отношения частот 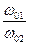— и разности начальных фаз φ₀₁ - φ₀₂ слагаемых колебаний (рис.8).

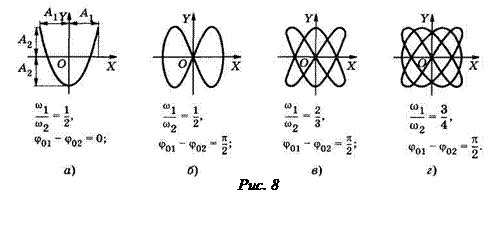Фигуры Лиссажу используют для настройки радиоизмерительной и ремонтной аппаратуры.