Влияние подоходного налога
Кроме аккордных налогов в экономике существуют подоходные (т.е. зависящие от уровня дохода) налоги. С их учетом потребительская функция будет иметь вид: C = C + mpc(Y – T – tY), где t - предельная налоговая ставка, которая показывает, на сколько увеличатся (уменьшатся) налоговые поступления при росте совокупного дохода на единицу, т.е.
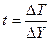 0 < t < 1
0 < t < 1
А поскольку Y= C + I + G, то, подставив в это равенство уравнение функции потребления, получим:
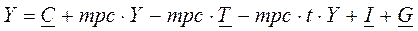
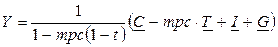 .
.
Следовательно, мультипликатор автономных расходов с учетом ставки подоходного налога t равен:
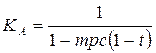 .
.
Величина мультипликатора при наличии ставки подоходного налога меньше, чем при его отсутствии (очевидно, что ((1 – mрc (1 – t) > (1 – mрc), а, как известно, чем больше знаменатель дроби, тем дробь меньше, т.е. 1 / (1 – mрc (1 – t) < 1 / (1 – mрc). Покажем это на числовом примере. Предположим, что mрc = 0.8, t = 0.1 (т.е. 10%). При отсутствии подоходного налога мультипликатор расходов равен 5 (1 / (1 – 0.8) = 5), а при появлении подоходного налога мультипликатор равен 3.57 (1 / (1 – 0.8 (1 – 0.1)) = 3.57).
 Изменение предельной налоговой ставки меняет наклон кривой совокупных планируемых расходов, который теперь будет равен [mрс (1 – t)]. Если t увеличивается, кривая Ep становится более пологой.
Изменение предельной налоговой ставки меняет наклон кривой совокупных планируемых расходов, который теперь будет равен [mрс (1 – t)]. Если t увеличивается, кривая Ep становится более пологой.
На рис.9.8. (а) представлена кривая совокупных планируемых расходов при отсутствии ставки подоходного налога, а на рис.4.8(б) – при ее наличии.
При наличии подоходного налога соответственно мультипликатор налогов равен: 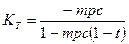 , а мультипликатор трансфертов:
, а мультипликатор трансфертов: 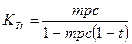 .Следует заметить, что когда появляется подоходный налог, мультипликатор сбалансированного бюджета (когда G = Т) не равен 1.
.Следует заметить, что когда появляется подоходный налог, мультипликатор сбалансированного бюджета (когда G = Т) не равен 1.
Докажем это: 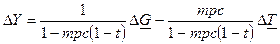 . Поскольку бюджет сбалансированный, то заменив Т на G и перегруппировав, получим:
. Поскольку бюджет сбалансированный, то заменив Т на G и перегруппировав, получим: 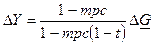 . Очевидно, что величина
. Очевидно, что величина 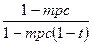 > 1, поскольку mрс < 1 и t < 1.
> 1, поскольку mрс < 1 и t < 1.
Дата добавления: 2016-07-27; просмотров: 2161;











