Построение векторной диаграммы
 | |||||
 | |||||
| |||||
Рис. 4. Векторная диаграмма для схемы на рис. 2
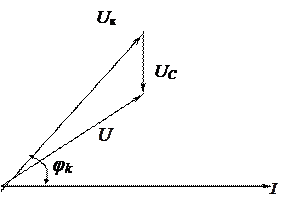 |
Рис. 5. Векторная диаграмма для схемы на рис. 3
При последовательном соединении элементов ток в них одинаков. Поэтому, построение векторной диаграммы начинают с вектора тока. Для этого выбирают масштабы по напряжению и по току:
MU = y [B/мм]; MI = x [A/мм].
При построении векторной диаграммы для схемы на рис. 4, вектор напря-жения Uк откладывают под углом φk в сторону опережения относительно вектора тока. Вектор падения напряжения на активном сопротивлении R (оно же – Rнг) будет совпадать по фазе с вектором тока I. Путем геометрического суммирования векторов напряжения Uк и Uнг можно получить вектор напря-жения на входе цепи U.
При построении векторной диаграммы для схемы на рис. 5 в качестве базового вектора также выбирается вектор тока I. Вектор напряжения Uк строится как и в предыдущем случае – под углом φк. Вектор падения напряжения на емкости UС отстает от тока на угол 90°. Геометрическая сумма этих векторов дает вектор напряжения на входе цепи. Векторная диаграмма, приведенная на рис. 5, построена для случая, когда ХL > ХC. Аналогично строятся векторные диаграммы для случаев ХL ≈ ХC; ХL < ХC .
Каждый студент строит три векторные диаграммы по указанию преподавателя, отметив, для какого наблюдения она построена. Кроме того, необходимо построить следующие графики:
I =ƒ(ХC), UС = ƒ(ХC), UL = ƒ(ХC), cos φ = ƒ(ХC) .
При построении графиков шкалы на осях координат должны быть кратны: 2; 2,5; 5 или 10, причем пересечение осей координат является нулем для всех масштабов.
При построении графиков по оси ординат берутся три шкалы: тока, напряжения и коэффициентов мощности. По оси абсцисс откладывается шкала ХC.
6. Подготовить отчет по работе.
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ЭЛЕМЕНТОВ R,L,С В ЦЕПИ ПЕРЕМЕННОГО ТОКА ОДНОФАЗНОЙ СИСТЕМЫ
В теории переменного тока для удобства изучения раскладывают вектор тока на две составляющие: активную Ia = Icosφ, совпадающую по фазе с вектором напряжения и реактивную Iр = Isinφ, перпендикулярную вектору напряжения.
Тогда
I= 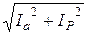 .
.
Часто активную составляющую Ia называют просто активным током, а реак-тивную Iр называют реактивным током.
Как известно, при параллельном соединении резисторов их проводимости складываются. Цепь переменного тока характеризуется следующими проводимостями: активной, реактивной и полной. Активная проводимость определяется как
g = R/Z2 [Cим].
Реактивная проводимость – b = X/Z2 = bL – bC [Сим].
Если реактивное сопротивление имеет индуктивный характер, то реак-тивная проводимость обозначается как bL, а если емкостной характер, то (– bC) и ей приписывается знак минус. Полная проводимость
y =1/Z= 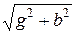 [Сим].
[Сим].
Таким образом
Ia = Icosφ = (U/Z)×(R/Z) = UR/Z2= Ug;
IР = Isinφ=(U/Z)×(XP/Z)= U XP /Z2=Ub;
I= 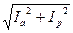 =U
=U 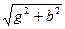 = U
= U 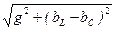 =UY;
=UY;
Y=U/I [См].
Если параллельно катушке индуктивности, имеющей внутри стальной
сердечник и обладающей реактивной проводимостью bL, подключать емкость с реактивной проводимостью bC и начать ее увеличивать, то при равенстве реактивных проводимостей катушки и конденсатора bL = bC , или bL – bC = 0 в схеме наступает так называемый резонанс токов. В этом случае полная прово-димость у=g оказывается наименьшей и, следовательно, ток в неразветвленной части цепи I = Ug =Ia также будет минимальным.
Как видно из последнего соотношения, ток в неразветвленной части цепи не содержит реактивной составляющей, следовательно, генераторы электри-ческой станции вырабатывают только активную мощность
S=UI=P.
В этом случае провода, подводящие электрическую энергию к такому приемнику, могут иметь меньшее сечение, чем в том случае, когда по ним течет ток, имеющий и реактивную составляющую. Включенные параллельно катушку индуктивности и батарею конденсаторов часто называют колебатель-ным контуром, т.к. в нем происходит переход (колебание) энергии магнитного поля катушки в энергию электрического поля конденсатора и наоборот. Каж-дую четверть периода энергия будет перераспределяться между катушкой индуктивности и конденсатором. В этом случае
IL = UbL; IC = Ubc, а так как bL = bC; то IL = IC .
Таким образом, в момент резонанса токов, реактивная составляющая тока катушки равна току конденсатора.
Мощность, потребляемая схемой, определяется по формуле
P = UIcosφ = UI = S
Явление резонанса тока в параллельной цепи широко применяется на практике для улучшения коэффициента мощности cosφ.
Улучшение коэффициента мощности имеет большое экономическое зна-чение, так как генераторы электрических станций в этом случае могут выраба-тывать только активную энергию, а реактивная образуется у потребителя в результате колебания энергии внутри колебательного контура..
1. Собрать схему (рис. 6)
2. Записать технические данные измерительных приборов и аппаратов в соответствующую таблицу протокола.
3. Определить цену деления приборов.
4. После тщательной проверки схемы студентами и преподавателем, пре-дупредив всех членов бригады, произвести включение схемы.
Включив и убедившись, что все приборы работают нормально, выполнять работу. Показания всех приборов записывать в табл. 4. Выполнение лабора-торной работы производится в следующей последовательности.
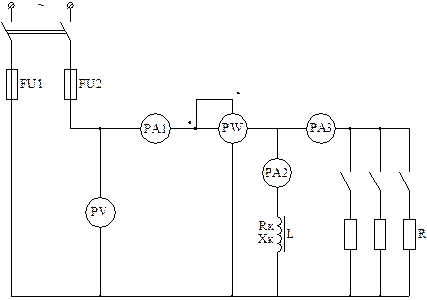
Рис. 6. Схема соединений – часть 1
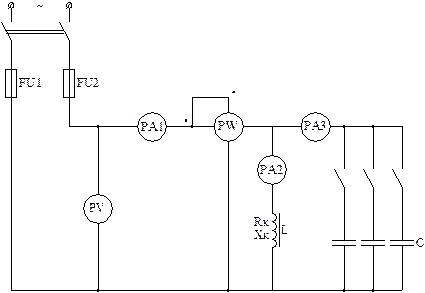
Рис. 7. Схема соединений – часть 2
6. Установить заданное напряжение. Первый опыт произвести при отклю-ченном активном сопротивлении. Только этот опыт позволяет определить активное Rк и индуктивное Xк сопротивления катушки, которые в после-дующих опытах остаются неизменными. Провести не менее пяти опытов, каждый раз увеличивая нагрузку (подключая дополнительные сопротивления).
7. Обработка результатов опытов.
Все параметры катушки индуктивности определяются из первого опыта при Iнг = 0. Эти параметры практически являются постоянными во время последующих опытов:
Z=U/I;
Zк=U/Iк ; Rк = P/Iк2; Xк= 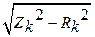 ;
;
bк = Xк/Zк2; cosφк= Rк/Zк = P/(UIк).
Далее определяем для последующих опытов:
Z=U/I; Y=1/Z ;
Rнг = U/Iнг;cos φ =P/(UI); S=UI.
По данным таблицы 4 построить три векторные диаграммы и графики зависимостей I, P, cos j = f (R нг) в одной системе координат.
Следует обратить внимание на степень сходимости результатов вычислений с соответствующими данными, полученными по векторным диаграммам.
Таблица 4
| Номер | Измерения | Вычисления | ||||||||||||||
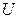
| Iнг | Iк | 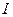
| 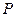
| 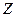
| Zк | Xк | Rнг | Rк | φк | 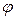
| Iа | Iр | 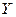
| 
| |
1. Собрать схему (рис. 6)
2. Записать технические данные измерительных приборов и аппаратов в соответствующую таблицу протокола.
3. Определить цену деления приборов.
4. После тщательной проверки схемы студентами и преподавателем, преду-предив всех членов бригады, произвести включение схемы.
Первый опыт произвести при отключенных конденсаторах. Как и в пре-дыдущем случае, этот опыт позволяет определить активное Rк и индуктивное Xк сопротивления катушки, которые в последующих опытах остаются неизменными. В последующих опытах следует последовательно подключать конденсаторы, набранные в батарею, и добиться резонанса (или состояния, близкого к нему). В момент резонанса (резонанса токов) показания амперметра в нераз-ветвленной части цепи минимальны.
Результаты расчетов записать в таблицу 5.
Таблица 5
| Номер | Измерения | Вычисления | ||||||||||||||
| Iс | Iк | 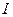
| 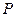
| 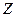
| Zк | Xк | Rк | 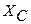
| φк | 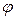
| Iа | Iр | 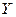
| 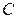
| |
5. Обработка результатов опытов. Все параметры катушки индуктивности определяются из первого опыта при IC = 0. Эти параметры практически являются постоянными:
Zк=U/Iк; Rк = P/Iк2; Xк= 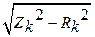 ; bк = Xк/Zк2;
; bк = Xк/Zк2;
cosφк= Rк/Zк = P/(UIк).
7. Далее, для последующих опытов определяем:
XC = U/IС ; bc = 1/XC ; R = U/IR; Z = U/I;
Y = 1/Z ; cos φ =P/(UI) ; XC = 1/( 2πƒC); C = 1/( 2πƒ XC);
ƒ= 50 Гц.
8. Построить в одной координатной системе графики зависимостей I, cos j = f(C).
9. Построить в масштабе векторные диаграммы до резонанса, в момент резонанса и после резонанса.
Дата добавления: 2020-10-14; просмотров: 655;











