Интегрирование уравнений методом Адамса
Пусть задано уравнение
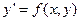
на отрезке 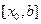 с начальными условиями
с начальными условиями 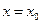 ,
, 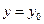 [ 11 ]. Разделим отрезок
[ 11 ]. Разделим отрезок 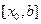 точками
точками 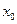 ,
, 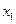 ,
, 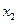 ,…
,… 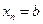 , на
, на 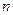 равных частей
равных частей 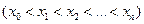 .
.
Обозначим приближенные значения решения в точках
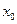 ,
, 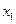 , …
, … 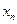
через
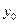 ,
, 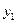 , …
, … 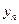 .
.
Вычислим разности первого порядка по следующим формулам
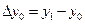 ,
,
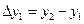 ,
,
...
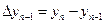 .
.
Вычислим разности второго порядка по следующим формулам
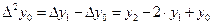 ,
,
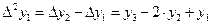 ,
,
...
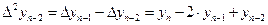 .
.
Вычислим разности вторых разностей, разности третьих разностей и т. д. по тем же правилам.
Обозначим через 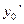 ,
, 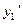 , …
, … 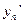 приближенные значения производных в точках
приближенные значения производных в точках 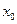 ,
, 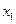 , …
, … 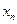 .
.
Обозначим через 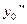 ,
, 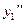 , …
, … 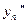 приближенные значения вторых производных в этих точках и т. д.
приближенные значения вторых производных в этих точках и т. д.
Вычислим первые разности производных по формулам
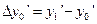 ,
,
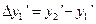 ,
,
...
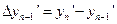 .
.
Вычислим вторые разности производных по формулам
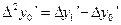 ,
,
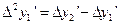 ,
,
...
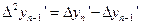 .
.
Последующие разности производных вычисляем по тем же правилам.
Напишем формулу Тейлора [ 10 ] для решения уравнения в окрестности точки 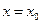
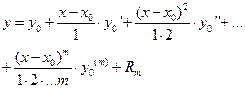 .
.
Значение 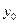 этой формуле известно. Значения
этой формуле известно. Значения 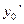 ,
, 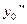 ,… производных находим из уравнения , дифференцируя члены этого уравнения по
,… производных находим из уравнения , дифференцируя члены этого уравнения по 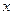 .
.
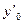 вычисляем по формуле
вычисляем по формуле 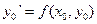 .
.
Далее, дифференцируя члены уравнения , и подставляя значения 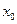 ,
, 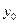 ,
, 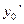 получим
получим
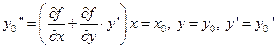 .
.
Далее, дважды дифференцируя члены уравнения , и подставляя значения 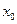 ,
, 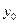 ,
, 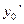 ,
, 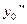 , получим
, получим 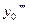 .
.
Выполняя такие действия, мы можем найти значения производных любого порядка при 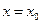 .
.
Таким образом, все члены кроме остаточного члена 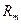 , известны. Пренебрегая остаточным членом, получим приближенное значение решения при любом значении
, известны. Пренебрегая остаточным членом, получим приближенное значение решения при любом значении 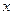 . Точность вычисления
. Точность вычисления 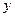 зависит от величины
зависит от величины 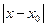 и числа членов в разложении.
и числа членов в разложении.
Используя формулу Тейлора, определим значения 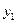 ,
, 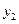 при
при 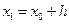 и
и 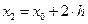 по следующим формулам
по следующим формулам
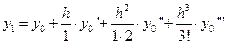
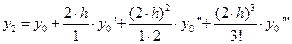
Используя величины 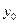 ,
, 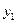 ,
, 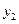 , определим
, определим
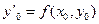 ,
, 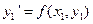 ,
, 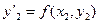 .
.
Используя величины 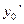 ,
, 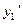 ,
, 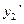 , определим
, определим
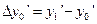 ,
, 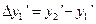 ,
, 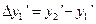 .
.
Допустим, что нам известны значения решения 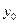 ,
, 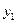 ,
, 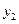 ,…
,… 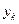 . На основании этих значений можно вычислить, используя уравнение , значения производных
. На основании этих значений можно вычислить, используя уравнение , значения производных 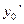 ,
, 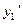 ,
, 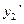 ,…
,… 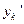 , а следовательно
, а следовательно
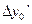 ,
, 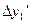 ,
, 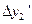 ,…
,… 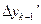 , и
, и
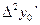 ,
, 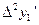 ,
, 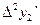 ,…
,… 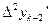 .
.
Определим значение 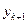 по формуле Тейлора, полагая
по формуле Тейлора, полагая
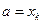 ,
, 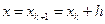 ,
,
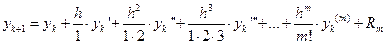 .
.
Ограничившись четырьмя членами разложения, получим
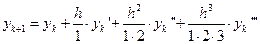 .
.
В этой формуле величины 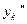 ,
, 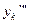 неизвестны. Их определяют через известные разности первого и второго порядков.
неизвестны. Их определяют через известные разности первого и второго порядков.
Представим по формуле Тейлора 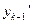 , полагая
, полагая 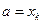 ,
, 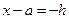 ,
,
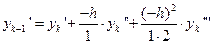 .
.
и 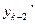 , полагая
, полагая 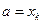 ,
, 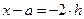 ,
,
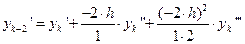 .
.
Из равенства найдем
. 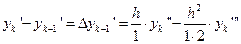
Вычитая из членов равенства члены равенства , получим
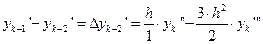 .
.
Из и находим
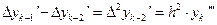 ,
,
или
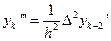 .
.
Подставляя выражение 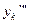 в равенство , получим
в равенство , получим
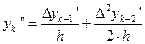
Подставляя и в разложение , получим
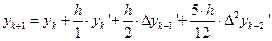
Это выражение называют формулой Адамса с четырьмя членами. Формула дает возможность, зная 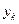 ,
, 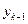 ,
, 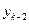 определить
определить 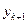 . Таким образом, зная
. Таким образом, зная 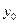 ,
, 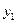 ,
, 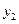 , возможно определить
, возможно определить 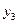 и далее
и далее 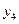 ,
, 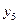 ...
...
Известно доказательство следующего утверждения. Если существует единственное решение уравнения на отрезке 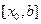 , то погрешность приближенных значений, определяемых по формуле , по абсолютной величине не превосходит
, то погрешность приближенных значений, определяемых по формуле , по абсолютной величине не превосходит 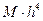 , где
, где 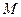 ‑ постоянная, зависящая от длины интервала и вида функции
‑ постоянная, зависящая от длины интервала и вида функции 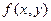 и не зависящая от величины
и не зависящая от величины 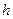 [ 10 ].
[ 10 ].
В том случае, когда необходима большая точность вычисления, то следует брать больше, чем в разложении , членов, и формула изменится. Если мы возьмем формулу, содержащую пять членов, то вместо формулы получим следующую формулу
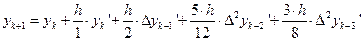 .
.
В этой формуле 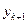 определяется через значения
определяется через значения 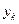 ,
, 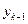 ,
, 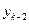 и
и 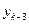 . Таким образом, чтобы начать вычисления по этой формуле, нужно знать четыре первых значения решения
. Таким образом, чтобы начать вычисления по этой формуле, нужно знать четыре первых значения решения 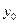 ,
, 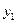 ,
, 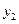 ,
, 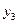 .
.
Рассмотрим пример нахождения приближенных значений решения уравнения 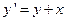 , удовлетворяющего начальному условию
, удовлетворяющего начальному условию 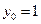 при
при 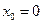 .
.
Значения решения определим при 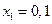 ,
, 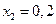 ,
, 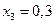 ,
, 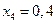 .
.
Сначала определим 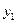 ,
, 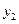 по формулам , . Из уравнения и начальных данных получим значение для
по формулам , . Из уравнения и начальных данных получим значение для 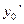
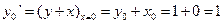 .
.
Дифференцируя данное уравнение, получим 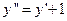 . Значение для
. Значение для 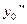 будет
будет
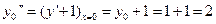 .
.
Дифференцируя еще раз данное уравнение, получим 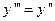 . Значение для
. Значение для 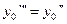 будет
будет 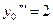 .
.
Подставляя в уравнение значения 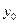 ,
, 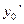 ,
, 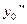 , и
, и 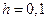 получим
получим
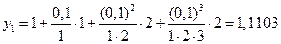 .
.
При 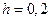 получим
получим
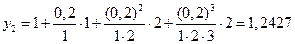 .
.
Зная 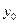 ,
, 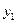 ,
, 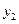 находим
находим
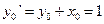 ,
,
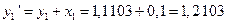 ,
,
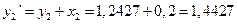 ,
,
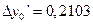 ,
,
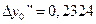 ,
,
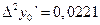 .
.
По формуле находим значение 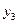
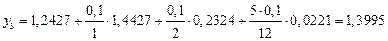 .
.
Далее находим значения 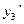 ,
, 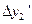 ,
, 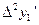 и по формуле находим значение
и по формуле находим значение 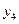
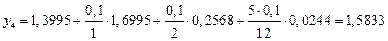 .
.
Точное решение заданного уравнения определяется выражением 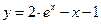 .
.
Следовательно, 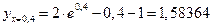 .
.
Абсолютная погрешность вычислений, по методу Адамса, равна 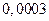 , а относительная погрешность равна
, а относительная погрешность равна 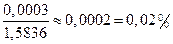 .
.
Абсолютная погрешность вычислений, по методу Эйлера, равна 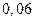 , а относительная погрешность равна
, а относительная погрешность равна 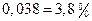 .
.
Дата добавления: 2020-10-14; просмотров: 414;











