Интегрирование системы уравнений
Пусть задана система двух уравнений с двумя искомыми функциями
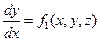 ,
,
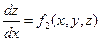 .
.
Требуется найти решения этой системы, удовлетворяющие начальным условиям 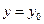 ,
, 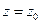 при
при 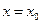 .
.
Будем определять значения функции 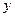 и
и 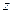 при значениях аргумента
при значениях аргумента 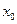 ,
, 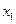 ,
, 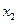 ,…
,… 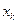 ,
, 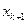 ,…
,… 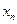 . Пусть
. Пусть
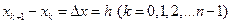 .
.
Приближенные значения функции обозначим
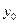 ,
, 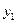 ,
, 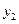 ,…
,… 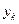 ,
, 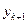 ,…
,… 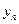
и соответственно
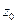 ,
, 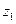 ,
, 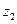 ,…
,… 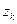 ,
, 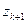 ,…
,… 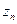 .
.
Рекуррентные формулы, по типу формул , выглядят следующим образом
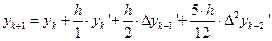 ,
,
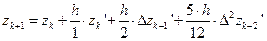 .
.
Для проведения вычислений по этим формулам нужно знать, кроме 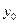 ,
, 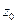 , значения
, значения 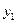 ,
, 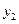 и
и 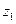 ,
, 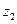 . Эти значения находим по формулам типа
. Эти значения находим по формулам типа
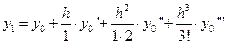 ,
,
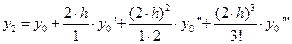 ,
,
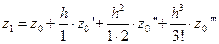 ,
,
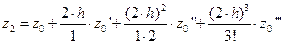 .
.
Для применения этих формул нужно знать 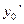 ,
, 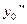 ,
, 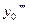 ,
, 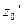 ,
, 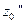 ,
, 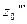 . Из уравнений и находим
. Из уравнений и находим
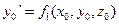 ,
,
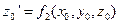 .
.
Дифференцируя уравнения и и подставляя значения 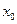 ,
, 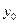 ,
, 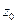 ,
, 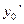 ,
, 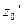 найдем
найдем
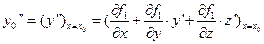 ,
,
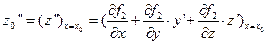 .
.
Дифференцируя еще раз, найдем 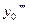 и
и 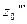 . Зная
. Зная 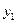 ,
, 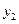 ,
, 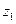 ,
, 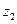 находим из уравнений и
находим из уравнений и
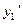 ,
, 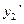 ,
, 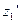 ,
, 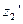 ,
, 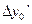 , ,
, , 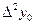 ,
, 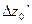 ,
, 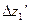 ,
, 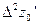 .
.
По формулам и найдем 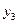 и
и 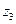 , а из уравнений и найдем
, а из уравнений и найдем 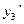 и
и 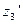 . Вычислив
. Вычислив 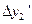 ,
, 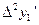 ,
, 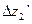 ,
, 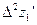 снова по формулам и найдем
снова по формулам и найдем 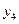 и
и 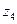 и т. д.
и т. д.
Рассмотрим пример нахождения приближенных значений решений системы уравнений 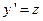 ,
, 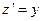 с начальными условиями
с начальными условиями 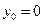 ,
, 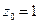 при
при 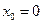 . Значения решения определим при
. Значения решения определим при 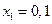 ,
, 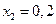 ,
, 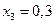 ,
, 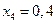 .
.
Из данных уравнений получим значения для 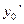 и
и 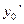
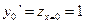 ,
,
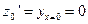 .
.
Дифференцируя данные уравнения, находим
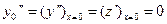 ,
,
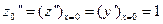 ,
,
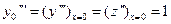 ,
,
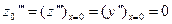 .
.
По формулам и находим
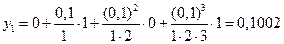 ,
,
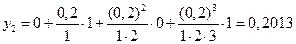 ,
,
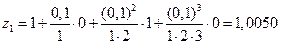 ,
,
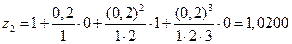 .
.
На основании данных уравнений находим
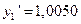 ,
, 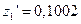 ,
,
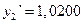 ,
, 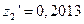 ,
,
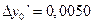 ,
, 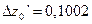 ,
,
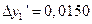 ,
, 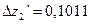 ,
,
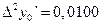 ,
, 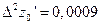 .
.
Далее по формулам и находим
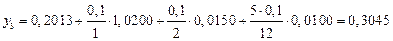 ,
,
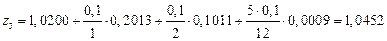 ,
,
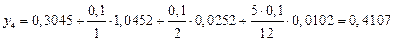 ,
,
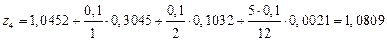 .
.
Известно решение этой системы уравнений 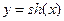 ,
, 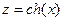 (гиперболические синус
(гиперболические синус 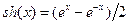 и косинус
и косинус 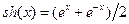 ). Поэтому пять верных, после запятой, знаков решений равны
). Поэтому пять верных, после запятой, знаков решений равны 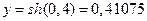 ,
, 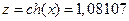 .
.
Так как уравнения высших порядков и системы уравнений высших порядков во многих случаях сводятся к системе уравнений первого порядка, то изложенные методы применимы к решению этих задач.
Дата добавления: 2020-10-14; просмотров: 333;











