Пятимерное пространство Хартсона
Теперь рассмотрим модель, называемую пятимерным пространством безопасности Хартстона [22]. В данной модели используется пятимерное пространство безопасности для моделирования процессов, установления полномочий и организации доступа на их основании. Модель имеет пять основных наборов:
А – установленных полномочий; U – пользователей; Е – операций; R – ресурсов; S – состояний.
Область безопасности будет выглядеть как декартово произведение: А×U×E×R×S. Доступ рассматривается как ряд запросов, осуществляемых пользователями u для выполнения операций e над ресурсами R в то время, когда система находится в состоянии s. Например, запрос на доступ представляется четырехмерным кортежем q = (u, e, R, s), u 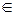 U,e
U,e 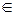 E,s
E,s 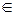 S,r
S,r 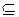 R. Величины u и s задаются системой в фиксированном виде. Таким образом, запрос на доступ – подпространство четырехмерной проекции пространства безопасности. Запросы получают право на доступ в том случае, когда они полностью заключены в соответствующие подпространства.
R. Величины u и s задаются системой в фиксированном виде. Таким образом, запрос на доступ – подпространство четырехмерной проекции пространства безопасности. Запросы получают право на доступ в том случае, когда они полностью заключены в соответствующие подпространства.
Процесс организации доступа можно описать алгоритмически следующим образом. Для запроса q, где q (u, e, R, s), набора U' вполне определенных групп пользователей, набора R' вполне определенных единиц ресурсов и набора P правильных (установленных) полномочий процесс организации доступа будет состоять из следующих процедур:
1. Вызвать все вспомогательные программы, необходимые для предварительного принятия решений.
2. Определить из U те группы пользователей, к которым принадлежит u. Затем выбрать из P спецификации полномочий, которым соответствуют выделенные группы пользователей. Этот набор полномочий F(u) определяет привилегию пользователя u.
3. Определить из P набор F(e) полномочий, которые устанавливают е как основную операцию. Этот набор называется привилегией операции е.
4. Определить из P набор F(R) (привилегию единичного ресурса R) – полномочия, которые определяют поднабор ресурсов из R', имеющего общие элементы с запрашиваемой единицей ресурса R.
Полномочия, которые являются общими для трех привилегий в процедурах 2, 3, 4, образуют D(q) (так называемый домен полномочий для запроса):
q: D(q)=F(u)∩F(e)F(R).
5. Удостовериться, что запрашиваемый ресурс R полностью включается в D(q), то есть каждый элемент из R должен содержаться в некоторой единице ресурса, которая определена в домене полномочий D(q).
6. Осуществить разбиение набора D(q) на эквивалентные классы так, чтобы два полномочия попадали в эквивалентный класс тогда и только тогда, когда они специфицируют одну единицу ресурса. Для каждого такого класса логическая операция ИЛИ (или И) выполняется с условиями доступа элементов каждого класса.
Новый набор полномочий – один на каждую единицу ресурса, указанную в D(q), есть F(u, q) - фактическая привилегия пользователя u по отношению к запросу q.
7. Вычислить ЕАС - условие фактического доступа, соответствующего запросу q, осуществляя логическое И (или ИЛИ) над условиями доступа членов F(u, q). Это И (или ИЛИ) выполняется над всеми единицами ресурсов, которые перекрывают единицу запрошенного ресурса.
8. Оценить ЕАС и принять решение о доступе:
- разрешить доступ к R, если R перекрывается;
- отказать в доступе в противном случае.
9. Произвести запись необходимых событий.
10. Вызвать все программы, необходимые для организации доступа после "принятия решения".
11. Выполнить все вспомогательные программы, вытекающие для каждого случая из условия 8.
12. Если решение о доступе было положительным – завершить физическую обработку.
Автор модели Хартстон отмечает, что приведенная последовательность шагов не всегда необходима в полном объеме. Например, в большинстве реализаций шаги 2 и 6 осуществляются во время регистрации пользователя в системе.
Дата добавления: 2020-10-14; просмотров: 717;











