Импульсные методы модуляции.

Все виды модуляции подразделяются на непрерывные и импульсные. Непрерывная модуляция - АМ, ЧМ и ФМ. Переносчиком сигнала является непрерывный сигнал с некоторой несущей частотой.

Импульсные виды модуляции используют переносчик в виде последовательности прямоугольных импульсов. Может изменяться в таком сигнале амплитуда импульса (АИМ - амплитудно-импульсная модуляция), частота импульса (ЧИМ - частотно-импульсная модуляция), ширина импульса (широтно-импульсная модуляция), фаза импульса, т.е. положение импульса относительно тактовых (синхронизирующих) моментов времени (ФИМ - фазово-импульсная модуляция).

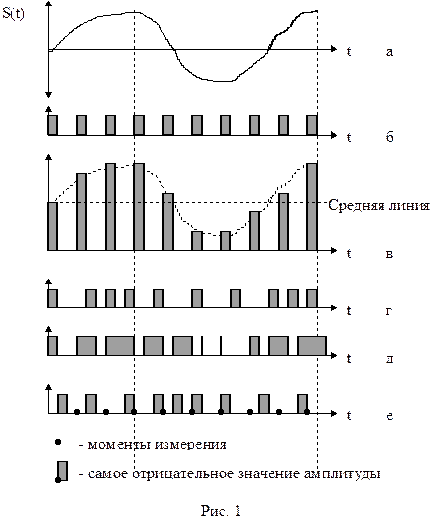
На рис.1 представлены временные диаграммы первичного аналогового сигнала (а), тактовая последовательность моментов времени (отсчетов) в виде синхронизирующих импульсов, вырабатываемых тактовым генератором -ТГ (б), и модулированные сигналы с использованием АИМ (в), ЧИМ (г), ШИМ (д) и ФИМ (е).

При АИМ амплитуда импульса соответствует амплитуде сигнала в момент измерения. Модулируется не несущая как при АМ модуляции, а тактовый импульс.

При ЧИМ частота следования импульсов пропорциональна амплитуде сигнала в точке отсчета.

При ШИМ ширина импульса определяется амплитудой сигнала в момент измерения.

При ФИМ расстояние импульса от момента измерения пропорциональна амплитуде сигнала.

Помимо импульсных методов модуляции имеется импульсно-кодовая модуляция (ИКМ), нашедшая наиболее широкое применение в современных системах электросвязи. ИКМ основана на кодировании амплитуд импульсов, полученных с использованием АИМ (рис. 2).

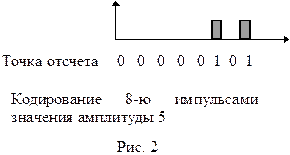
АИМ, ЧИМ, ШИМ, ФИМ требуют прецизионной аппаратуры формирования амплитуды (для АИМ), либо очень тонкой синхронизации для ЧИМ, ШИМ и ФИМ.

ИКМ требует синхронизирующую частоту, фиксированную по количеству кодирующих импульсов (обычно 8-мь на один отсчет).

Теорема отсчета

Философски непрерывных процессов и сигналов нет. Непрерывность обусловлена разрешающей способностью наблюдателя или прибора наблюдения. Чем выше разрешающая способность, тем фиксируются более мелкие изменения в плоть до наблюдения скачкообразности казалось бы непрерывного процесса (движения колеса на плоскости при наблюдении с точностью до движения молекул или кристаллической решетки покажет скачкообразность).

Любой сигнал можно разложить на составляющие синусоидальные колебания, используя разложение в ряд Фурье. Физически разложение сигнала можно наблюдать для световых сигналов. Спектральные линии доказывают объективное существование различных гармоник в сложных сигналах.

Пусть приемник сигнала воспринимает максимальную гармонику с частотой Fmax. За пределами этой частоты сигнал не распознается (ультразвуковые частоты, ультрафиолетовые для человеческих органов чувств не досягаемы). Период Tmin=1/Fmax будет минимальным среди периодов всех воспринимаемых частот. В течении периода гармоника имеет положительную полуволну и отрицательную. Размер амплитуды каждой полуволны можно измерять. Таким образом, интервал измерений значений непрерывного сигнала не стоит делать меньше полуволны, т. к. более мелкие интервалы будут уже за пределами разрешения приемника. Этот интервал измерений называют интервалом отсчета. Т.о.

tотс=Tmin/2=1/2*Fmax.

Теорема отсчета или как ее называют у нас "теорема Котельникова", а в США "теория отображения Найквиста" гласит: для восстановления исходного непрерывного сигнала достаточно иметь количество точек отсчета не менее удвоенной максимальной частоте исходного сигнала в канале.

Строгий вывод этой теоремы достаточно сложен. Базируется он на задании некоторого такого изменения значения сигнала, меньше которого изменения не фиксируются (предел чувствительности).Мы же получили такой же результат только логически, зная о разложении сигнала на гармоники, и о разрешающей способности приемника.