КОДЫ ДВОИЧНЫХ ЧИСЕЛ
- Разрядная сетка
Все данные в центральной части ЭВМ хранятся и обрабатываются в виде двоичных кодов. Для размещения кода отводится строго фиксированное число двоичных разрядов, образующих разрядную сетку. Без привязки к разрядной сетке понятие кода не определено. Каждый разряд кода нумеруется, начиная с нуля. В разных ЭВМ принята разная система нумерации. В универсальных ЭВМ разряды нумеруются слева направо, а в мини и микро-ЭВМ – справа налево. Пример нумерации для n двоичных разрядов приведен ниже.
| Номера ß разрядов ß | a0 | a1 | a2 | … | an-2 | an-1 | Универсальные ЭВМ |
| 2n-1 2n-2 2n-3 ….. 21 20 | Вес разрядов | ||||||
| an-1 | an-2 | … | a2 | a1 | a0 | Мини и микро-ЭВМ |
При любой системе нумерации левый разряд имеет наибольший вес, а правый – наименьший. Положение точки, отделяющей целую и дробную часть, подразумевается. В большинстве ЭВМ считается, что точка находится после младшего разряда. В этом случае в разрядной сетке размещаются коды целых чисел.
Наиболее просто кодируются целые числа без знака. В этом случае в разрядную сетку записывается двоичное представление числа. Каждая цифра числа занимает разряд в соответствии со своим весом.
Для кодирования целых чисел со знаком применяют:
· Прямой код.
· Обратный код.
· Дополнительный код.
Прямой код
Прямой n-разрядный двоичный код состоит из знакового разряда и
n-1 разрядов для записи модуля числа. В качестве знакового разряда используется старший разряд.
| an-1 | an-2 | ... | a0 |

Знак “плюс” кодируется как 0, а знак “минус” – как 1.
Определим диапазон чисел, представимых в прямом n-разрядном двоичном коде. Введем следующие обозначения: A+max – максимальное положительное число, A-min - минимальное отрицательное число:
A+max = 2n-1 – 1; A-min = -(2n-1-1)
Пример: Получить прямой 5-ти разрядный код числа A[10] = -6.Определить диапазон чисел для этой разрядной сетки.
1.| A[10] | = 6 Þ | A[2] | = 0110 (на запись модуля выделено 4 разряда)
2.Знаковый разряд = 1
|
Определим диапазон чисел:
A+max = 24 – 1 = 15 A-max = -(24 – 1) = -15
Пример: Получить прямой 8-ми разрядный код числа A[16] = 3С. Определить диапазон чисел для этой разрядной сетки.
1.| A[16] | = 3С Þ | A[2] | = 0111100 (на запись модуля выделено 7 разрядов)
2.Знаковый разряд = 0
|
Определим диапазон чисел:
A+max = 27 – 1 = 127 A-max = -(27 – 1) = -127
Прямой код для кодирования целых чисел со знаком в ЭВМ практически не применяется и используется как составная часть более сложных кодов.
Недостатки:
1. Сложение и вычитание чисел в прямом коде выполняется по правилам алгебры:
(С)пр = (А)пр + (В)пр
(С)пр = (А)пр - (В)пр ,
поэтому процессор должен иметь два разных устройства: сумматор и вычитатель.
2. Знаковый разряд обрабатывается отдельно от остальных по особым правилам.
3. Неоднозначность кодировки нуля:




|




|
Обратный код
Обратный код предполагает, что при кодировании числа и выполнении операций с кодами используются одинаковые правила обработки всех разрядов, включая знаковый. Обратный n-разрядный двоичный код – это код образованный по правилу:
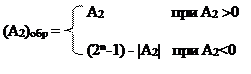 |
Операция вида (2n – 1) - |A2| дает дополнение до наибольшего числа без знака, представимого в в n-разрядной сетке. Другими словами, кодирование числа можно выполнить следующим образом:
· Для положительного числа в n-разрядную сетку записывается его двоичное представление.
· Для отрицательного числа в n-разрядную сетку записывается разность между наибольшим числом без знака и модулем кодируемого числа.
В обоих случаях значение знакового разряда будет получено автоматически.
|
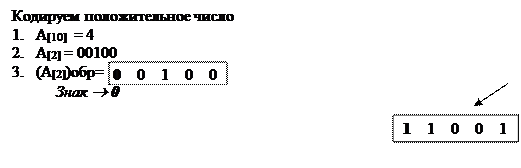 |
Замечания:
v Операция дополнения для двоичного обратного кода эквивалентна инверсии всех разрядов. Инверсия удобна для реализации в операционном устройстве.
v Если длина разрядной сетки кратна 4, дополнение удобно вычислять в шестнадцатеричной системе счисления. Такая разрядная сетка характерна для большинства ЭВМ.
v Если длина разрядной сетки кратна 3, дополнение удобно вычислять в восьмеричной системе счисления. Такая разрядная сетка не характерна для ЭВМ. Однако для мини-ЭВМ с 16-ти разрядной сеткой при документировании программ часто пользуются восьмеричной записью кодов чисел, при этом старший разряд рассматривается как двоичная цифра.
Пример: Определить обратный код числа А[10] = -21 при n=16.
Получим обратный код во всех трех указанных формах. Так как кодируется отрицательное число, необходимо вычислить дополнение и использовать его в качестве обратного кода.
v Двоичное кодирование.
1. |А[10]| = 21
2. |А[2]| = 10101
3. |А[2]| = 0000 0000 0001 0101 (Это модуль кодируемого числа в разрядной сетке)
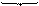
 4. (А[2])обр= 1111 1111 1110 1010
4. (А[2])обр= 1111 1111 1110 1010
F F E A[16]
v Шестнадцатеричное кодирование
1. | А[10]| = 21
|А[16]| = 15
2. (А[16])обр =F F F F (Это максимальное число без знака)
- 0 0 1 5(Это модуль кодируемого числа в разрядной сетке)
F F E A
v Восьмеричное кодирование
1. | А[10]| = 21
|А[8]| = 25
2. (А[8])обр =1 7 7 7 7 7(Это максимальное число без знака)
- 0 0 0 0 2 5(Это модуль кодируемого числа в разрядной сетке)
1 7 7 7 5 2
Диапазон чисел в обратном коде составляет: A+max = 2n-1 – 1; A-min = -(2n-1-1)
Достоинства:
1 Сложение и вычитание можно выполнять на одном устройстве: сумматоре, поскольку вычитание может быть заменено сложением с дополнением вычитаемого:
(С)обр = (А)обр + (В)обр
(С)обр = (А)обр - (В)обр = (А)обр + ((В)обр)обр
2 Знаковый разряд обрабатывается по общим правилам. Его значение при выполнении операции устанавливается автоматически.
Недостатки:
Неоднозначность кодировки нуля:




|




|
Чаще всего в ЭВМ используется модификация обратного кода – дополнительный код.
Дополнительный код
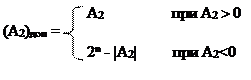 |
Дополнительный код обладает всеми достоинствами обратного и устраняет его главный недостаток – неоднозначность кодирования нуля. Дополнительный n-разрядный двоичный код представляет собой код, образованный по правилу:
Операция 2n – |A2| называется операцией дополнения до следующего за большим числом без знака для данной разрядной сетки. Другими словами, кодирование числа можно выполнить следующим образом:
· Для положительного числа в n-разрядную сетку занести его двоичное представление.
· Для отрицательного числа в n-разрядную сетку занести разность между следующим
за большим числом без знака и модулем кодируемого числа.
Дополнение при использовании дополнительного кода больше по значению на 1 от дополнения при использовании обратного кода:
( 2n – 1 ) - |A2| + 1 = 2n - |A2|
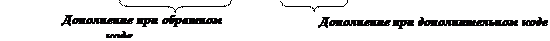 |
Cледствие: дополнительный код отрицательного числа может быть получен из его обратного кода путем прибавления единицы в младший разряд.
Пример: Определить дополнительный код числа А[16] = -1D8 при n=16.
Кодируется отрицательное число, следовательно, необходимо вычислить дополнение и использовать его в качестве кода.
v Двоичное кодирование.
1. |А[16]| = 1D8
2. |А[2]| = 111011000
3. |А[2]| = 0000 0001 1101 1000 (Это модуль кодируемого числа в разрядной сетке)
4. (А[2])обр= 1111 1110 0010 0111 (Это обратный код)
+ 1
 (А[2])доп= 1111 1110 0010 1000 (Это дополнительный код)
(А[2])доп= 1111 1110 0010 1000 (Это дополнительный код)
F E 2 8[16]
v Шестнадцатеричное кодирование
1. | А[16]| = 1D8
2. (А[16])обр F F F F (Это максимальное число без знака)
- 0 1 D 8(Это модуль кодируемого числа в разрядной сетке)
F E 2 7 (Это обратный код)
+ 1
(А[16])доп= F E 2 8 (Это дополнительный код)
v Восьмеричное кодирование
1. | А[8]| = 730
2. (А[8])обр =1 7 7 7 7 7(Это максимальное число без знака)
- 0 0 0 7 3 0(Это модуль кодируемого числа в разрядной сетке)
1 7 7 0 4 7 (Это обратный код)
+ 1
(А[8])доп= 1 7 7 0 5 0 (Это дополнительный код)
Дополнительный код обеспечивает однозначное представление нуля:
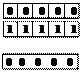 +0 при n=5
+0 при n=5
-0 при n=5
+ 1
Диапазон представимых чисел в дополнительном коде: A+max = 2n-1 – 1; A-min = -2n-1
Дата добавления: 2019-02-08; просмотров: 2023;











