Построение гистограммы для стационарной системы.

Г - эмпирическая плотность распределения вероятностей. Задаются границы изменения интересующей характеристики. у_i®[y_н;у_в], числом интервалов N_g. Определяется ширина интервала D=( y_н -_­ у_в)/N_g.

Затем в процессе моделирования по мере появления значений у_i определяется число попаданий этой случайной величины в каждый из интервалов R_i гистограммы. По этим данным вычисляется относительная частота по каждому интервалу: G_i=R_i/(N*D), где N - общее число измерений у. Площадь гистограммы равна единице, равна сумме площадей:

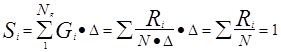, т.к.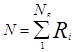

При необходимости выдвигается гипотеза о том, что эмпирическое распределение согласуется с некоторым теоретическим распределением. Эта гипотеза проверяется по тому или иному критерию. Например, при использовании критерия c² в качестве меры расхождения используется выражение 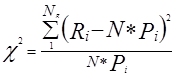(6);

где - 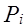определяется из выбранного теоретического распределения вероятность попадания случайной величины в i-ый интервал.

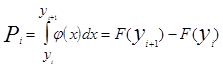(7).

Из теоремы Пирсона следует, что для любой функции распределения F(y) случайной величины упри N®¥ распределения величины c² имеет вид:

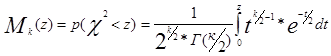, где z - значение случайной величины c² ,

k=N_g-(r +1) - число степеней свободы распределения c² . r - количество параметров теоретического распределения, Г(к/2) - гамма функция.

Функция распределения c² табулирована. По вычисленному значению c² и числу степеней свободы с помощью таблиц определяется вероятность Р(c²<Z). Если она превышает заданный уровень значимости С, то выдвинутая гипотеза принимается.