Основные подходы к построению ММ систем.
Исходной информацией при построении ММ процессов функционирования систем служат данные о назначении и условиях работы исследуемой (проектируемой) системы S. Эта информация определяет основную цель моделирования, требования к ММ, уровень абстрагирования, выбор математической схемы моделирования.
Понятие математическая схема позволяет рассматривать математику не как метод расчёта, а как метод мышления, средства формулирования понятий, что является наиболее важным при переходе от словесного описания к формализованному представлению процесса её функционирования в виде некоторой ММ.
При пользовании мат. схемой в первую очередь исследователя системы должен интересовать вопрос об адекватности отображения в виде конкретных схем реальных процессов в исследуемой системе, а не возможность получения ответа (результата решения) на конкретный вопрос исследования.
Например, представление процесса функционирования ИВС коллективного пользования в виде сети схем массового обслуживания даёт возможность хорошо описать процессы, происходящие в системе, но при сложных законах входящих потоков и потоков обслуживания не даёт возможности получения результатов в явном виде.
Математическую схему можно определить как звено при переходе от содержательного к формализованному описанию процесса функционирования системы с учётом воздействия внешней среды. Т.е. имеет место цепочка: описательная модель — математическая схема — имитационная модель.
Каждая конкретная система S характеризуется набором свойств, под которыми понимаются величины, отображающие поведение моделируемого объекта (реальной системы) и учитываются условия её функционирования во взаимодействии с внешней средой (системой) Е.
При построении ММ системы S необходимо решить вопрос о её полноте. Полнота моделирования регулируется, в основном, выбором границ "Система S — среда Е". Также должна быть решена задача упрощения ММ, которая помогает выделить основные свойства системы, отбросив второстепенные в плане цели моделирования.
ММ объекта моделирования, т.е. системы S можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества:
- совокупность Х - входных воздействий на S хiÎХ, i=1…nx;
- совокупность воздействий внешней среды vlÎV, l=1…nv;
- совокупность внутренних (собственных) параметров системы hkÎH, k=1…nh;
- совокупность выходных характеристик системы yjÎY, j=1…ny.
В перечисленных множествах можно выделить управляемые и неуправляемые величины. В общем случае X, V, H, Y не пересекаемые множества, содержат как детерминированные так и стохастические составляющие. Входные воздействия Е и внутренние параметры S являются независимыми (экзогенными) переменными, 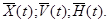 Выходные характеристики - зависимые переменные (эндогенные)
Выходные характеристики - зависимые переменные (эндогенные) 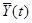 . Процесс функционирования S описывается оператором FS:
. Процесс функционирования S описывается оператором FS:
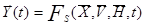 (1)
(1)
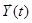 - выходная траектория. FS - закон функционирования S. FS может быть функция, функционал, логические условия, алгоритм, таблица или словесное описание правил.
- выходная траектория. FS - закон функционирования S. FS может быть функция, функционал, логические условия, алгоритм, таблица или словесное описание правил.
Алгоритм функционирования AS — метод получения выходных характеристик 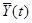 с учётом входных воздействий
с учётом входных воздействий 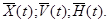 Очевидно один и тот же FS может быть реализован различными способами, т.е. с помощью множества различных AS.
Очевидно один и тот же FS может быть реализован различными способами, т.е. с помощью множества различных AS.
Соотношение (1) является математическим описанием поведения объекта S моделирования во времени t, т.е. отражает его динамические свойства. (1) - это динамическая модель системы S. Для статических условий ММ есть отображения X, V, H в Y, т.е. 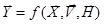 (2)
(2)
Соотношения (1), (2) могут быть заданы формулами, таблицами и т.д.
Также соотношения в ряде случаев могут быть получены через свойства системы в конкретные моменты времени, называемые состояниями.
Состояния системы S характеризуются векторами:
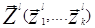 и
и 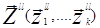 , где
, где 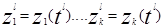 в момент tlÎ(t0, T)
в момент tlÎ(t0, T)
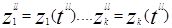 в момент tllÎ(t0, T) и т.д. к=1…nZ.
в момент tllÎ(t0, T) и т.д. к=1…nZ.
Z1(t), Z2(t)… Zk(t) - это координаты точки в к-мерном фазовом пространстве. Каждой реализации процесса будет соответствовать некоторая фазовая траектория.
Совокупность всех возможных значений состояний { 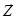 } называется пространством состояний объекта моделирования Z, причём zkÎZ.
} называется пространством состояний объекта моделирования Z, причём zkÎZ.
Состояние системы S в интервале времени t0<t£Tl полностью определяется начальными условиями 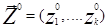 , где
, где 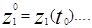 входными
входными 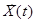 , внутренними параметрами
, внутренними параметрами 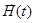 и воздействиями внешней среды
и воздействиями внешней среды 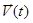 , которые имели место за промежуток времени t* - t0 c помощью 2-х векторных уравнений:
, которые имели место за промежуток времени t* - t0 c помощью 2-х векторных уравнений:
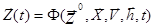 ; (3)
; (3)
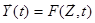 . (4)
. (4)
иначе: 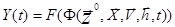 . (5)
. (5)
Время в мод. S может рассматриваться на интервале моделирования (t0, T) как непрер., так и дискретное, т.е. квантованное на отрезке длин. Dt.
Таким образом под ММ объекта понимаем конечное множество переменных { 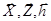 } вместе с математическими связями между ними и характеристиками
} вместе с математическими связями между ними и характеристиками 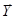 .
.
Моделирование называется детерминированным, если операторы F, Ф детерминированные, т.е. для конкретного входа выход детерминированный. Детерминированное моделирование - частный случай стохастического моделирования. В практике моделирование объектов в области системного анализа на первичных этапах исследования рациональнее использовать типовые математические схемы: диф. уравнения, конечные и вероятностные автоматы, СМО и т.д.
Не облад. такой степенью общности, как модели (3), (4), типовые математические схемы имеют преимущество простоты и наглядности, но при существенном сужении возможности применения.
В качестве детерминированных моделей, когда при исследовании случайный факт не учитывается, для представления систем, функционирующих в непрерывном времени, используются дифференциальные, интегральные и др. уравнения, а для представления систем, функционирующих в дискретном времени — конечные автоматы и конечно разностные схемы.
В начале стохастических моделей (при учёте случайного фактора) для представления систем с дискретным временем используются вероятностные автоматы, а для представления систем с непрерывным временем — системы массового обслуживания (СМО). Большое практическое значение при исследовании сложных индивидуальных управленческих систем, к которым относятся АСУ, имеют так называемые агрегативные модели.
Aгрегативные модели (системы) позволяют описать широкий круг объектов исследования с отображением системного характера этих объектов. Именно при агрегативном описании сложный объект расчленяется на конечное число частей (подсистем), сохраняя при этом связи, обеспечивая взаимодействие частей.
Дата добавления: 2019-02-08; просмотров: 716;











