Методы расчета надежности невосстанавливаемых систем

При расчете вероятности безотказной работы, средней наработки до возникновения первого отказа элементы системы рассматриваются как невосстанавливаемые. В этом случае, если структура системы сводится к основному или резервному соединению элементов, при условии, что работа одного из параллельно соединенных элементов обеспечивает работоспособное состояние системы, показатели безотказности последней определяются по показателям безотказности элементов с использованием классического метода расчета надежности.

Поскольку при основном соединении элементов (см. рис. 3.1,а) работоспособное состояние системы имеет место при совпадении работоспособных состояний всех элементов, то вероятность этого состояния системы определяется произведением вероятностей работоспособных состояний всех элементов [16]. Если система состоит из п последовательно включенных элементов, то при вероятности безотказной работы каждого из элементов р_i(t) вероятность безотказной работы системы

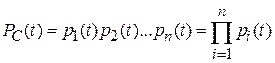. (3.1)

При параллельном соединении элементов и при условии, что для работы системы достаточно работы одного из включенных параллельно элементов, отказ системы является совместным событием, имеющим место при отказе всех параллельно включенных элементов. Если параллельно включены т элементов (см. рис. 3.1,б) и вероятность отказа каждого q_j(t) = 1 – p_j(t), то вероятность отказа этой системы

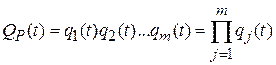. (3.2)

Если структурная схема надежности системы состоит из последовательно и параллельно соединенных элементов, то расчет ее надежности может быть произведен с использованием (3.1), (3.2). Так, для системы, структурная схема надежности которой представлена на рис. 3.1,в, вероятность безотказной работы:

.

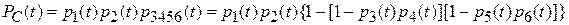Чтобы определить значение средней наработки системы до отказа и другие показатели надежности, требуется знать законы распределения времени безотказной работы элементов (наработки до отказа) системы. Поскольку на участке нормальной эксплуатации с удовлетворительной точностью в качестве закона распределения времени безотказной работы элементов может быть принят экспоненциальный, то при основном соединении элементов, если 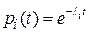выражение (3.1) примет следующий вид:

,

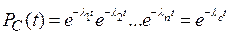где .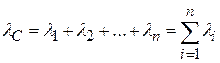

Таким образом, при основном соединении элементов, имеющих экспоненциальный закон распределения времени безотказной работы, закон распределения времени безотказной работы системы также будет экспоненциальным, в соответствии с этим имеем

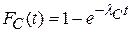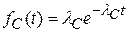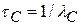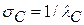; ; ; (3. 4)

При резервном соединении т элементов, имеющих экспоненциальный закон распределения времени безотказной работы, вероятность отказа группы параллельно включенных элементов

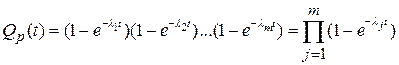. (3.5)

Если все элементы равнонадежны и 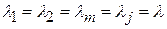, то

; .

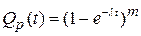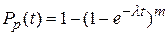Таким образом, при резервном соединении элементов экспоненциальный закон распределения времени безотказной работы не сохраняется.

Рассмотренный метод расчета широко применяют для оценки надежности локальных систем и элементов, входящих в их состав. На стадии проектирования при известных интенсивностях отказов элементов оценивают вероятность безотказной работы системы и предусматривают мероприятия, направленные на ее повышение и заключающиеся в резервировании наименее надежных и наиболее ответственных элементов, облегчении условий эксплуатации, снижении уровня нагрузки и др.

Анализируют надежность на стадии проектирования обычно в несколько этапов. На первом этапе, проводимом на стадии составления технического задания на локальную систему или отдельное техническое средство, когда их структуры еще не определены, производится прикидочная оценка надежности. Она исходит из априорной информации о надежности близких по характеру систем и элементов, с помощью которых они могут быть реализованы. На втором этапе проводится ориентировочная оценка надежности. При этом известны структура системы и входящие в ее состав элементы, их показатели надежности, заданные при нормальных (номинальных) условиях эксплуатации.

Окончательный расчет надежности технических средств, иногда называемый коэффициентным, проводится на стадии завершения технического проекта, когда проведена эксплуатация опытных образцов устройства и известны условия эксплуатации всех элементов. Последние определяются уровнем нагрузок, характером изменения таких влияющих величин, как температура окружающей и регулируемой среды, уровень вибрации, колебания напряжения питания и частоты, колебания влажности и др. Учет этих величин позволяет произвести коррекцию значений интенсивностей отказов элементов. Так, их работа при пониженных нагрузках приводит к снижению интенсивностей отказов.

Влияние отклонения этих величин на интенсивность отказов учитывают путем использования поправочных коэффициентов k_i

,

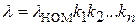где 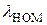– номинальное значение интенсивности отказов, соответствующее нормальным условиям эксплуатации; k₁, k₂ ,..., k_n – поправочные коэффициенты, учитывающие отклонения влияющих величин от нормальных значений.

Следует отметить, что достоверные данные по поправочным коэффициентам известны только для радиоэлектронных элементов, что позволяет производить окончательный расчет структурной надежности устройств, включающих эти элементы. По общепромышленным средствам АСУ ТП эти данные в подавляющем большинстве случаев отсутствуют. Последнее в значительной мере определяется разнообразием условий эксплуатации устройств в различных отраслях промышленности и сложностью получения этих данных.

Во многих случаях рассмотренный выше способ расчета надежности не может быть использован, так как не всегда схема надежности содержит последовательно-параллельное соединение элементов.

Существуют несколько разновидностей классического метода расчета надежности систем со сложной структурой, часть из которых будет рассмотрена на практических занятиях.