Особенности расчета поля в дальней зоне антенны
Выражения (3), (7) на первый взгляд просты; однако при произвольном положении точки наблюдения процесс интегрирования или суммирования не позволяет получать простых замкнутых выражений, допускающих наглядную трактовку. Сложность эта связана, прежде всего, с тем, что поле каждого излучающего элемента известно в своей собственной системе координат, связанной с самим излучателем. Для нахождения результирующего поля необходимо ввести единую для всех элементов систему координат и выразить поля всех элементов в этой общей системе координат.
Наибольший практический интерес при излучении антенны представляет электромагнитное поле, создаваемое на большом расстоянии от нее (так называемая дальняя зона антенны). Сформулировать суть упрощений, допускаемых при расчете поля на большом расстоянии, а также оценить это расстояние можно следующим образом.
Рассмотрим систему из дискретных излучателей, одинаково ориентированных в пространстве, а именно так, что любой излучающий элемент может быть совмещен с другим только путем параллельного перемещения в пространстве без вращения. Введем общую прямоугольную систему координат х, у, z, центр которой расположим внутри излучающей системы. Выделим произвольный элемент с номером n (рис. 3), находящийся на расстоянии 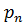 от начала общей системы координат.
от начала общей системы координат.
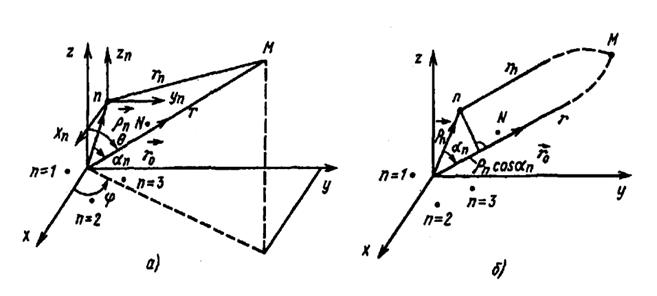
Рисунок 3. Поле элемента n
Оси локальной системы координат 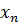 ,
, 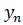 ,
, 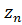 ориентируем параллельно соответствующим осям системы координат х, у, z. Введем также общую сферическую систему координат r,
ориентируем параллельно соответствующим осям системы координат х, у, z. Введем также общую сферическую систему координат r, 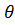 ,
, 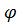 . В системе координат
. В системе координат 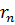 ,
, 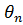 ,
, 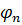 каждая компонента поля излучения рассматриваемого элемента имеет вид
каждая компонента поля излучения рассматриваемого элемента имеет вид
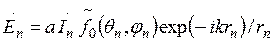 . (8)
. (8)
Необходимо все функции, входящие в (8) и зависящие от координат 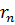 ,
, 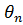 ,
, 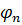 выразить через r,
выразить через r, 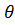 ,
, 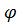 . С особой осторожностью следует подойти к замене
. С особой осторожностью следует подойти к замене 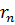 на r в фазовом множителе exp(
на r в фазовом множителе exp( 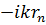 ), поскольку даже небольшое отличие
), поскольку даже небольшое отличие 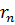 от r может привести к большим фазовым ошибкам. Так, если ρn составляет всего 15 мм, то на частоте f =10 ГГц (λ = 3 см) максимальная фазовая ошибка при замене
от r может привести к большим фазовым ошибкам. Так, если ρn составляет всего 15 мм, то на частоте f =10 ГГц (λ = 3 см) максимальная фазовая ошибка при замене 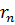 на r независимо от абсолютного значения r может составить значение
на r независимо от абсолютного значения r может составить значение 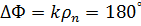 .
.
Дата добавления: 2019-02-08; просмотров: 852;











