Растяжение (сжатие) стержней

Пусть стержень нагружен произвольной продольной нагрузкой. Вырежем на некотором расстоянии z бесконечно малый элемент dz (рис.40). На данный элемент действует внешняя нагрузка и внутренние продольные силы в сечениях, по которым вырезан элемент.

Рис.40

Составим уравнение равновесия вырезанного элемента.

- N + q_z×dz + N + dN = 0,

,

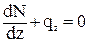N’ + q_z = 0. (92)

Решение данного дифференциального уравнения с правой частью состоит из двух частей общего и частного решения и имеет вид

N(z) = C - 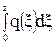(93)

Определим физический смысл постоянной интегрирования. При z=0:

N(0)=C.

Значение интеграла зависит от внешней приложенной нагрузки. Рассмотрим значения интеграла нагрузочных функций для наиболее часто встречающихся нагрузок.

а) сосредоточенная сила (рис.41):

Рис.41

при z£a Ф_N(z)=0

при z³a Ф_N(z)=-P

б) распределенная нагрузка (рис.42):

Рис.42

при z£c Ф_N(z)=0

при z³c Ф_N(z)=-q(z-c)

Пример.

Для заданной схемы нагружения стержня (рис.43) построить эпюру продольной силы N(z) при следующих исходных данных: q=10 кН/м, l=1м.

Рис.43

Решение.

1. Совместим начало системы координат с левым концом стержня и направим координатную ось z вдоль его продольной оси.

В соответствии со схемой нагружения разделим стержень на три участка и запишем уравнение продольных сил следующим образом:

N (z) = N (0) - 2q·z│₁+2q (z - l) │₂ + q (z - 2l) │_3.

В этом уравнении приняты следующие обозначения:

N(0) – значение продольной силы в начале координат (реакция опоры),

z – координата сечения, в котором определяется значение продольной силы.

Для решения задачи необходимо определить одну неизвестную величину – N(0). Для этого запишем граничное условие: N (3l) = 0.

Напомним, что граничные условия – это известные значения интегральных характеристик в какой-либо точке стержня.

Для определения неизвестной реакции N(0) необходимо приравнять уравнение продольных сил к нулю, подставив в нем вместо координаты «z» координату «3l»:

N (0)-2q (3l) + 2q (3l – l) + q (3l – 2l) = 0.

Решая это уравнение, найдем: N (0) = 10 кН.

2. Построение графика продольных сил.

При построении графиков уравнение рассматривается на каждом участке в отдельности и вместо координаты «z» подставляется соответствующая координата начала и конца рассматриваемого участка.

1 участок - 0 ≤ z ≤ l:

N (0) =10 кН,

N (l) = 10 – 2·10·1 = -10 кН.

2 участок - l ≤ z ≤ 2l:

N (l) = 10 – 2·10·1 + 2·10(l – l) = -10 кН,

N (2l) = 10 – 2·10·2 + 2·10(2 – 1) = -10 кН.

3 участок - 2l ≤ z ≤ 3l:

N (2l) = 10 – 2·10·2 + 2·10(2 – 1) + 10(2 – 2) = -10 кН,

N (3l) = 10 – 2·10·3 + 2·10(3 – 1) + 10(3 – 2) = 0 кН.

По рассчитанным значениям строится график продольной силы (рис. 43).

Кручение стержней

Пусть стержень нагружен произвольной крутящей нагрузкой. Вырежем на некотором расстоянии z бесконечно малый элемент dz (рис.44). На данный элемент действует внешняя нагрузка и внутренние крутящие моменты в сечениях, по которым вырезан элемент.

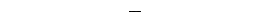
Рис.44

Составим уравнение равновесия вырезанного элемента.

- М_к + m_z×dz + М_к + dМ_к = 0,

,

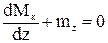М_к’ + m_z = 0. (94)

Решение данного дифференциального уравнения с правой частью состоит из двух частей общего и частного решения и имеет вид

M_к(z) = C - 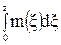(95)

Определим физический смысл постоянной интегрирования. При z=0

М_к(0)=C.

Значение интеграла зависит от внешней приложенной нагрузки. Рассмотрим значения нагрузочных функций для наиболее часто встречающихся нагрузок.

а) сосредоточенный момент (рис.44):

Рис.44

при z£a Ф_м(z)=0

при z³a Ф_м(z)=-L

б) распределенная нагрузка (рис.45):

Рис.45

при z£c Ф_м(z)=0

при z³c Ф_м(z)=-m(z-c)

Пример.

Для приведённой схемы нагружения прямого стержня (рис.46) построить эпюру крутящего момента при следующих исходных данных: m_z = 10 кН/м, L = 10 кНм,

l = 1 м.

Решение.

В соответствии со схемой нагружения запишем уравнение крутящего момента в следующем виде:

M_k (z) = M_k (0) │₁ - L│₂ - m_z(z-2l) │₃ .

Исходя из условий закрепления стержня, запишем следующее граничное условие: M_k (0) = 0 (реакция незакреплённого конца стержня равна нулю).

Рис.46

Таким образом, записанное уравнение не содержит неизвестных величин и можно приступать к построению графика. Построение графика будем производить аналогично построению графика в примере 1.

1 участок - 0 ≤ z ≤ l:

M_k (0) = 0 кНм,

M_k (l) = 0 кНм.

2 участок - l ≤ z ≤ 2l:

M_k (l) = 0 – 10 = -10 кНм,

M_k (2l) = 0 – 10 = -10 кНм.

3 участок - 2l ≤ z ≤ 3l:

M_k (2l) = 0 – 10 – 10(2 – 2) = - 10 кНм,

M_k (3l) = 0 – 10 – 10(3 – 2) = -20 кНм.

По рассчитанным значениям строится график крутящего момента (рис. 46).

Изгиб стержней.

Пусть стержень нагружен произвольной поперечной нагрузкой. Вырежем на некотором расстоянии z бесконечно малый элемент dz (рис.47). На данный элемент действует внешняя нагрузка и внутренние поперечные силы и изгибающие моменты в сечениях, по которым вырезан элемент.

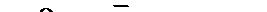
Рис.47

Составим уравнения равновесия вырезанного элемента.

Уравнение равновесия всех сил на вертикальную ось.

- Q_y + q_y×dz + Q_y + dQ_y = 0,

,

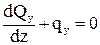Q_y’ + q_y = 0. (96)

Уравнение равновесия моментов относительно центра тяжести правого сечения вырезанного элемента.

- М_х + q_y×dz×dz/2 + М_х + dМ_х - Q_y×dz = 0,

слагаемое, выражающее момент от распределенной нагрузки, второго порядка малости, поэтому им можно пренебречь

,

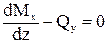М_х’ = Q_y. (97)

Объединяя дифференциальные уравнения (96) и (97), получим:

М_х'' = - q_y (98)

Решение данного дифференциального уравнения с правой частью состоит из двух частей общего и частного решения и имеет вид

М_х(z) = C₁+С₂z – Ф_м,

где Ф_м – частное решение, отражающее внешнюю приложенную нагрузку.

Определим физический смысл постоянных интегрирования. При z=0

М_х(0) = C₁,

М_х’(0) = Q_y(0) = С₂.

Рассмотрим подробнее частное решение. Пусть стержень нагружен произвольной распределенной нагрузкой (рис.48). Определим величину поперечной силы и изгибающего момента для точки с координатой z.

Рис.48

Q_y = ,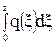

М_х = 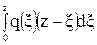. (99)

Значения интегралов зависят от внешней приложенной нагрузки. Рассмотрим значения нагрузочных функций для наиболее часто встречающихся нагрузок.

а) сосредоточенная сила (рис.49):

Рис.49

при z£a Ф_Q(z)=0

Ф_М(z)=0

при z³a Ф_Q(z)=-P

Ф_М(z)=-P(z-a)

б) распределенная нагрузка (рис.50):

Рис.50

при z£c Ф_Q(z)=0

Ф_М(z)=0

при z³c Ф_Q(z)=-q(z-c)

Ф_М(z)=-q(z-c)²/2

в) сосредоточенный момент (рис.51):

Рис.51

при z£b Ф_Q(z)=0

Ф_М(z)=0

при z³b Ф_Q(z)=0

Ф_М(z)=-L

Пример.

Для заданной схемы нагружения стержня (рис.52) построить эпюры поперечной силы Q_y(z) и изгибающего момента M_x(z) при следующих исходных данных: L = 5 кНм, P = 10 кН, q = 20 кН/м, l = 1 м.

Рис.52

Решение.

Запишем уравнения поперечных сил и изгибающего момента:

Q_y (z) = Q_y(0) │₁ – P - q×(z - l) │₂

M_x (z) = M_x (0) + Q_y(0)×z│₁ - P×(z - l) - q×(z - l)²/2│₂

В соответствии с условиями закрепления стержня запишем граничные условия в следующем виде: M_x (0) = - L,

M_x (3l) = 0.

Для нахождения неизвестной реакции Q_y (0) необходимо приравнять уравнение изгибающего момента к нулю при координате z = 3l:

M_x (3l) = M_x (0) + Q_y (0)×3l - P×(3l - l) - q×(3l - l)²/2 = 0.

Решая это уравнение относительно Q_y (0), получим Q_y (0) = 21.67кН.

Теперь, учитывая найденные константы, уравнения интегральных характеристик можно переписать в следующем виде:

Q_y (z) = 21.67│₁ – P – q×(z - l) │₂

M_x (z) = -L + 21.67z│₁ – P×(z - l) – q×(z - l)²/2│₂

Построение графиков будем производить аналогично примеру 1.

1 участок 0 ≤ z ≤ l:

Q_y (0) = 21.67 кН,

Q_y (l) = 21.67 кН,

M_x (0) = -5 кНм,

M_x (l) = -5 + 21.67*1 = 16.67 кНм.

2 участок l ≤ z ≤ 3l:

Q_y (l) = 21.67 – 10 = 11.67 кН,

Q_y (3l) = 21.67 – 10 – 20*(3 - 1) = -28.33 кН,

M_x (l) = -5 + 21.67*1 – 10(1 – 1) – 20(1 – 1) = 16.67 кНм,

M_x (3l) = -5 + 21.67*3 – 10(3 – 1) – 20(3 – 1) =0 кНм.

Определим координаты экстремума и значения функции изгибающего момента в экстремальной точке:

Q_y (z1) = 21.67 – P – q (z1 - l) = 0 → z1 = 1.58 м.

M_x (1.58) = -L + 21.67·1.58 – P (1.58 - l) – q (1.58 - l)²/2 = 20.07 кНм.

По рассчитанным значениям строятся графики поперечной силы и изгибающего момента (рис. 52).