Постановка транспортної задачі та її математична модель
Транспортна задача полягає у пошуку найбільш вигідного плану перевезення однорідного продукту з пунктів виробництва (чи зберігання) до пунктів споживання, тобто від постачальників до споживачів, ефективність якого будемо оцінювати за критерієм найменшої вартості перевезення. Транспортна задача - це специфічна задача лінійного програмування.
Сформулюємо визначення транспортної задачі. Деяку однорідну продукцію, яка знаходиться в тпостачальників А1, А2, ..., Аткількістю a1, а2, ..., атодиниць відповідно, потрібно перевезти пспоживачам В1, В2, ..., Впв кількостях b1, b2, ..., bn одиниць. Відома матриця вартостей перевезення одиниці продукції від i-го постачальника до j-го споживача:
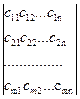
Необхідно скласти такий план перевезення, щоб вивезти всю продукцію від постачальників, задовольнити потреби всіх споживачів і сумарна вартість перевезення при цьому має бути мінімальною.
Окреслена постановка задачі вимагає виконання рівності загальної суми запасу вантажу загальній сумі потреб в ньому, тобто
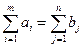(5.1)
Якщо в транспортній задачі умова (5.1) виконується, то таку транспортну задачу називають закритою (з правильним балансом). Якщо ж рівність (5.1) не виконується, то транспортну задачу називають відкритою (з неправильним балансом). Побудуємо математичну модель транспортної задачі. Оскільки наперед невідомо, скільки вантажу потрібно перевезти від певного постачальника до споживача, щоб план перевезень був оптимальним, то позначимо його через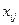 
. Вартість перевезення всього вантажу від постачальників до споживачів позначимо Z. Умову транспортної задачі можна записати у вигляді таблиці:
| постачальники | Споживачі | В1 | В2 | … | Вп |
 Потреби Запаси
| b1 | b2 | … | bn | |
| A1 | a1 |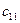 
| 
| … | 
|
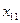
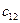
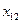
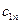
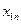
| A2 | a2 |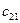 
| 
| … | 
|
| … | … | … | … | … | … |
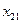
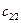
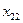
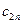
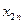
| Am | am |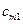 
| 
| … | 
|
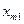
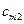
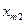
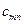
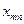
Тоді цільова функція матиме вигляд:
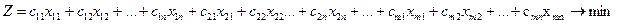
або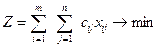 
(5.2)
Для складання обмежень транспортної задачі скористаємося такими міркуваннями:
1) кількість вантажу, який потрібно перевезти до пункту Вjз усіх пунктів постачання, рівна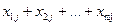 
aспоживачеві Вjпотрібно bj-одиниць вантажу, тому, враховуючи те, що всі потреби повинні бути задоволеними, можемо записати обмеження стосовно потреб:
, 
;
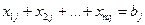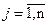2) кількість вантажу, який треба вивезти з пункту постачання Аiдо всіх споживачів, дорівнює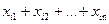 
а постачальник має 
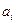одиниць вантажу і всі вантажі мають бути вивезені, тому обмеження стосовно запасів матимуть вигляд:
. 
.
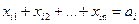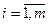В загальному випадку систему обмежень запишемо таким чином:
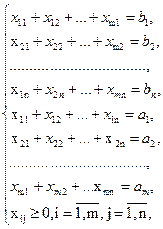
або
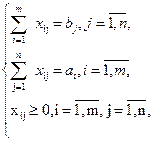(5.3)
Ми отримали математичну модель транспортної задачі (5.2)-(5.3), де 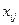- кількість продукції, що перевозиться від і-гопостачальника до j-го споживача; 
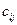- вартість перевезення одиниці продукції від i-го постачальника до j-го споживача; 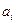- запаси продукції i-го постачальника; bj - попит на продукцію j-го споживача.
Тепер, виходячи з економічної постановки транспортної задачі, можемо сформулювати її математичну задачу: серед всіх невід’ємних розв’язків системи рівнянь (5.3) знайти такий, при якому оптимізуюча форма (5.2) набуде найменшого значення.
Транспортна задача є задачею лінійного програмування, яку можна розв’язати симплекс-методом, але при розв’язуванні транспортної задачі симплексним методом ми б отримали симплекс-таблиці великих розмірів, оскільки число невідомих дорівнює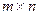 
. Специфічна структура цієї задачі дозволяє використати для її розв’язання ефективніший метод - метод потенціалів, який розглянуто в п. 5.3.
5.2. Методи побудови початкового опорного плану
Як і в симплексному методі розв’язування задач лінійного програмування, при розв’язуванні транспортної задачі потрібно мати початковий опорний план.
Розглянемо методи знаходження цього плану:
1. Діагональний метод (північно-західного кута).
Побудову початкового опорного плану за методом північно-західного кута починають із заповнення лівої верхньої клітинки таблиці A1B1 (х11), в яку записують менше з двох чисел а1 та b1. Далі переходять до наступної клітинки в рядку або стовпчику і заповнюють її і т.д., закінчуючи останньою правою клітинкою таблиці AmBn (хmn).
Розглянемо алгоритм побудови початкового опорного плану транспортної задачі методом північно-західного кута:
1. Перевірка транспортної задачі на закритість. Якщо вона відкрита, то приводимо її до задачі закритого типу введенням або фіктивного постачальника або фіктивного споживача.
2. Першою заповнюємо верхню ліву клітинку. Заповнення клітинки AiBj таблиці здійснюємо за такими правилами:
а) якщо аi<bj, тобто запаси менші від потреб, то в цю клітинку записуємо весь об’єм запасу вантажу аi, перераховуємо потреби споживача Bj, постачальника Ai вилучаємо з розгляду (наприклад, поставивши у всіх клітинках рядочка, крім заповненої, прочерки) і переходимо до заповнення наступної клітинки Ai+1Bj;
б) якщо аi>bj, тобто запаси більші від потреб, то в цю клітинку записуємо весь об’єм потреб вантажу bj, перераховуємо запаси постачальника Ai, вилучаємо з розгляду споживача Bj (ставимо у всіх клітинках стовпчика, крім заповненої, прочерки) і переходимо до заповнення наступної клітинки AiBj+1;
в) якщо аi=bj, тобто запаси рівні потребам, то в цю клітинку записуємо весь об’єм потреб чи запасів, вилучаємо з розгляду постачальника Ai і споживача Bj (ставимо в усіх клітинках стовпчика і рядка, крім заповненої, прочерки) і переходимо до заповнення наступної клітинки Ai+1Bj+1.
3. Серед незаповнених клітинок (без обсягу вантажу і прочерків) знову вибираємо верхню ліву клітинку таблиці і заповнюємо її за правилами, поданими в п. 2. Так продовжуємо до тих пір, доки не заповнимо всі клітинки таблиці.
4. З одержаної таблиці виписуємо початковий опорний план транспортної задачі та обчислюємо значення цільової функції при цьому плані.
2. Метод найменшої вартості.
Правила знаходження початкового опорного плану транспортної задачі методом найменшої вартості відрізняються від правил знаходження такого плану діагональним методом тільки послідовністю вибору клітинки, яку потрібно заповнювати. Згідно з методом найменшої вартості першою вибирається клітинка з найменшою вартістю перевезення одиниці вантажу від постачальника до споживача. Якщо таких клітинок декілька, то вибираємо ту, для якої кількість вантажу, що можна перевезти, найбільша.
Після побудови початкового опорного плану кожним з методів у таблиці ма’ бути заповнено (т+п-1) клітинок, тому що ранг матриці системи обмежень транспортної задачі рівний r=m+n-l, де т- кількість постачальників, п - кількість споживачів. Заповнені клітинки називаються базисними, а незаповнені - вільними. Якщо кількість базисних клітинок рівна (т+п-1), то такий план називається невиродженим. Якщо кількість заповнених клітинок менша (т+п-1), то план називається виродженим. Тоді необхідно заповнити відповідну кількість порожніх (небазисних) клітинок, записуючи в них «нульове перевезення», і ці клітинки вважати базисними. Коли ж кількість заповнених клітинок перевищує (т+п-1), то початковий опорний план побудовано неправильно і він не є опорним.
Метод потенціалів
5.3.1. Критерій оптимальності опорного плану за методом потенціалів
Ми вже знаємо методи знаходження початкових опорних планів транспортної задачі, але чи ці опорні плани є оптимальними, тобто такими, що дають найменшу загальну вартість перевезення всього вантажу від постачальників до споживачів, ми не знаємо. Опорний план перевіряють на оптимальність за допомогою потенціалів. Відповідно до кожного постачальника Aі ставимо потенціал uі aкожному споживачу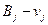 
.
Критерій оптимальності опорного плану транспортної задачі
якщо для деякого опорного плану (хіj) транспортної задачі існують такі числа-потенціали uі та vj що для базисних клітинок виконуються рівності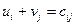 
, а для небазисних клітинок виконуються нерівність 
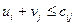для всіх 
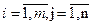, то такий опорний план є оптимальним.
Потенціали опорного плану визначаються із рівнянь системи 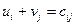,які записують для всіх заповнених клітинок таблиці транспортної задачі. За допомогою розрахованих потенціалів перевіряють умову оптимальності 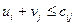- для незаповнених клітинок таблиці. Якщо хоча б для однієї небазисної клітинки ця умова не виконується, тобто 
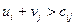, то поточний план не є оптимальним і потрібно перейти до нового опорного плану.
Дата добавления: 2016-07-22; просмотров: 3151;
Поиск по сайту
Узнать еще
- Автоматна модель шифратору
- Автомодельного ламинарного течения жидкости в трубе с использованием системы дифференциальных уравнений, описывающих течение жидкости в трубе
- Адаптационная модель К. Рой
- Аддитивная цветовая модель
- Анализ и постановка задач
- АНАЛИЗ СОВОКУПНОГО СПРОСА И СОВОКУПНОГО ПРЕДЛОЖЕНИЯ. МОДЕЛЬ «AD-AS»
- Аналитическая модель решения задачи
- Багатосегментна модель
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
